 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение. Матрица называетсяхарактеристической матрицейматрицы А
|
|
Матрица 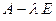 называется характеристической матрицей матрицы А.
называется характеристической матрицей матрицы А.
Многочлен 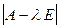 называется характеристическим многочленом, а уравнение
называется характеристическим многочленом, а уравнение 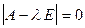 называется характеристическим уравнением матрицы Аили характеристическим уравнением оператора
называется характеристическим уравнением матрицы Аили характеристическим уравнением оператора  .
.
Равенство (3) показывает, что все собственные значения линейного оператора  и только они являются корнями его характеристического многочлена.
и только они являются корнями его характеристического многочлена.
Кратностью собственного значения 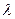 линейного оператора
линейного оператора  называют кратность, с которой
называют кратность, с которой 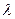 входит в качестве корня в характеристический многочлен оператора
входит в качестве корня в характеристический многочлен оператора  .
.
Вернемся к системе (2). Видим, что вектор 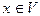 тогда и только тогда есть собственный вектор оператора
тогда и только тогда есть собственный вектор оператора  , принадлежащий собственному значению
, принадлежащий собственному значению 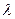 , когда координатная строка
, когда координатная строка 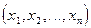 вектора х является ненулевым решением системы (2).
вектора х является ненулевым решением системы (2).
Задача. Найти собственные значения и соответствующие им собственные векторы линейного оператора  пространства
пространства 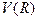 , если в некотором базисе оператор
, если в некотором базисе оператор  задан матрицей
задан матрицей
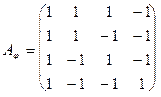
Решение. Составим характеристическое уравнение 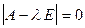 оператора
оператора  и найдем его корни. Действительные корни этого уравнения есть собственные значения оператора
и найдем его корни. Действительные корни этого уравнения есть собственные значения оператора
 .
. 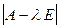 =
=
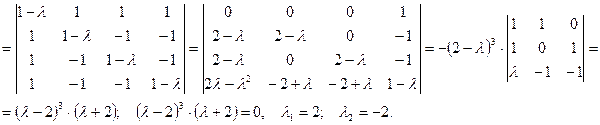
Собственными векторами, принадлежащими собственному значению 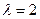 будут те и только те ненулевые векторы, которые удовлетворяют условию
будут те и только те ненулевые векторы, которые удовлетворяют условию 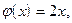 то есть являются решениями системы (2) при
то есть являются решениями системы (2) при 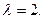
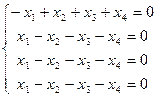 Общее решение системы
Общее решение системы 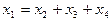 .
.
Составим фундаментальную систему решений:
| х 1 | х 2 | х 3 | х 4 |
| (1 (1 (1 | 0) = а 1 0) = а 2 1) = а 3 |
Пространство решений этой системы 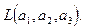
Множество собственных векторов, принадлежащих собственному значению 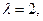 есть
есть 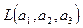 \
\ 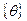 . Собственными векторами для
. Собственными векторами для 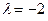 будут те и только те ненулевые векторы, которые удовлетворяют условию
будут те и только те ненулевые векторы, которые удовлетворяют условию 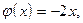 то есть являются решениями системы (2) при
то есть являются решениями системы (2) при 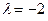 .
.
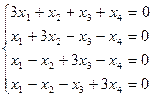 Общее решение системы:
Общее решение системы: 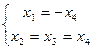
Составим фундаментальную систему решений:
| х 1 | х 2 | х 3 | х 4 |
| (-1 | 1) = b |
пространство решений системы L(b).
Множество собственных векторов, принадлежащих собственному значению 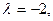 есть L(b)\
есть L(b)\ 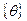 .
.
Дата публикования: 2015-07-22; Прочитано: 153 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
