Понятие двойственных задач линейного программирования

Как в линейном программировании, так и в математическом программировании, существует понятие двойственности, которое позволяет унифицированным образом установить взаимосвязи для различных методов анализа математических моделей на чувствительность.

Рассмотрим две задачи линейного программирования:

1. максимизировать целевую функцию:

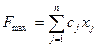, (1)

если задана следующая система ограничений:

(2)

2. минимизировать целевую функцию:

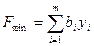, (3)

при заданной системе ограничений:

(4)

Назовем первую задачу (соотношения (1) и (2)) прямой задачей линейного программирования, а вторую (соотношения (3) и (4)) – двойственной задачей линейного программирования по отношению к первой.

В качестве иллюстрации к сказанному рассмотрим следующий пример:

Пусть задана некоторая прямая задача линейного программирования:

Максимизировать целевую функцию:

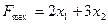
при условии:

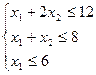
Тогда задача линейного программирования, двойственная по отношению к данной, будет выглядеть следующим образом:

Минимизировать целевую функцию:

при условии:

Грубо говоря, двойственная задача – это в некотором смысле транспонированная прямая задача линейного программирования. Так, j-тый столбец, составленный из коэффициентов, фигурирующих в неравенствах линейных ограничений математической модели прямой задачи линейного программирования, полностью совпадает с j-той строкой, составленной из коэффициентов, фигурирующих в неравенствах линейных ограничений математической модели двойственной задачи линейного программирования. Строка, составленная из коэффициентов в выражении для целевой функции, совпадает со столбцом, составленным из констант, фигурирующих в правых частях неравенств линейных ограничений математической модели двойственной задачи. В свою очередь, столбец, составленный из констант, фигурирующих в правых частях неравенств линейных ограничений математической модели прямой задачи линейного программирования, совпадает со строкой, составленной из коэффициентов в выражении для целевой функции математической модели двойственной задачи. Направление знаков неравенства в математической модели прямой задачи линейного программирования противоположно направлению знаков в математической модели двойственной задачи. Кроме того, требование максимизации в математической модели прямой задачи линейного программирования заменено в математической модели двойственной задачи требованием минимизации.

Введя обозначения:

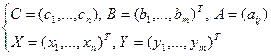(5)

прямую и двойственную по отношению к ней задачи линейного программирования можно записать в векторном виде.

Прямая задача:

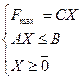(6)

Двойственная задача:

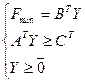(7)

Следует отметить, что задача линейного программирования, двойственная к задаче (7), совпадает с исходной задачей линейного программирования (6).

Можно показать, что если в прямой задаче линейного программирования есть ограничения типа равенства, то в двойственной задаче им соответствуют переменные, которые не ограничены в знаке. В свою очередь, если в прямой задаче линейного программирования есть переменные, которые не ограничены в знаке, то в двойственной задаче им соответствуют ограничения типа равенства.

Имеет место следующая теорема:

Теорема двойственности.

Если прямая и двойственная по отношению к ней задачи линейного программирования имеют допустимые решения, то:

1. существует оптимальное решение прямой задачи ;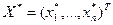

2. существует оптимальное решение двойственной задачи ;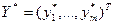

3. имеет место следующее соотношение:

(8)

Если прямая задача оптимальное решение, для которого значение целевой функции ограничено, то соответствующая ей двойственная задача допускает оптимальное решение при том же значении целевой функции. В свою очередь, если двойственная задача допускает оптимальное решение, для которого значение целевой функции ограничено, то соответствующая ей прямая задача допускает оптимальное решение при том же значении целевой функции.

Прежде чем приступить к доказательству изложенной теоремы двойственности, покажем, что любое допустимое решение задачи линейного программирования накладывает ограничение на оптимальное значение целевой функции соответствующей двойственной задачи.

Пусть переменные 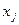удовлетворяют ограничениям математической модели прямой задачи линейного программирования, а переменные удовлетворяют ограничениям математической модели двойственной задачи. Умножим каждое i-тое ограничение прямой задачи на , а каждое j-тое ограничение двойственной задачи на 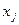. Так как 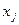и принимают неотрицательные значения, то направление неравенств в результате такой операции сохранятся неизменными. Сложив отдельно правые и соответственно левые части всех соотношений, полученных в результате применения вышеописанной процедуры к ограничениям прямой задачи, получим:

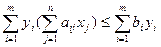(9)

Действую аналогично, но только в отношении ограничений двойственной задачи линейного программирования, получим следующее соотношение:

(10)

Так как выражения в левых частях неравенств (9) и (10) совпадают, имеет место следующее неравенство:

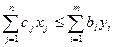(11)

Таким образом, получаем, что значение целевой функции, соответствующее некоторому допустимому решению (оптимальному или не оптимальному) прямой задачи линейного программирования, не является независимым от значения целевой функции для любого допустимого решения (оптимального или не оптимального) соответствующей ей двойственной задачи.

решение, то соответствующая ей двойственная задача не имеет ни одного допустимого решения. Предположим, что существует допустимое решения прямой задачи линейного программирования, для которого значение целевой функции оказывается неограниченно большим. В этом случае двойственная задача не обладает ни одним допустимым решением. Если бы в такой ситуации двойственная задача имела бы хотя бы одно допустимое решение, то возникло бы неразрешимое противоречие. Из-за справедливости неравенства (11) решение двойственной задачи ограничивало бы сверху значение целевой функции для любого допустимого решения примой задачи. Но согласно сделанному предположению, значение целевой функции прямой задачи может быть произвольно большим.

Важно отметить, что помимо всего прочего теорема двойственности позволяет проверить на оптимальность любое допустимое пробное решение прямой задачи. Если существует допустимое решение двойственной задачи, для которого значение целевой функции совпадает со значением целевой функции прямой задачи, то решение обоих задач является оптимальным. Справедливость этого утверждения непосредственно следует из соотношения (11).