 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Аналитический метод решения задачи линейного программирования. Симплекс-метод
|
|
Выделим такой класс задач линейного программирования, который отвечает следующим требованиям:
A: найти наибольшее значение целевой функции, то есть 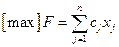
B: любое ограничение из Ω имеет знак “≤”, то есть 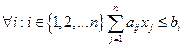
C: неотрицательные значения переменных, то есть 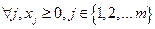
D: неотрицательные значения свободных членов в Ω, то есть 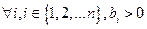
Для этого класса задач введем понятие основной задачи линейного программирования:
| (max F, Ω) | 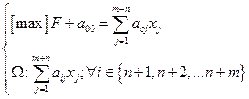
|
где 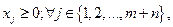
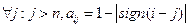
Вновь введенные переменные xj (m+n ≥ j ≥ n+1)
Обозначающие разность между левой и правой частью неравенства, будем называть базисными. Остальные переменные называют свободными, а множество индексов, которыми помечены базисные переменные называют базисом (В). В нашем примере
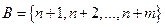
Пример: Задана задача линейного программирования.
| [max] F = | c1x1+c2x2+c0 a11x1 + a12x2 ≤ b1 a21x1 + a22x2 ≤ b2 |
Перейти у основной задаче линейного программирования
Решение
| [max] F – a00 = | a01*x1+a02*x2+0*x3+0*x4 a31*x1+a32*x2+1*x3+0*x4 = a30 a41*x1+a42*x2+0*x3+1*x4 = a40 |
,где
a0j = cj , a3j = a1j , a4j = a2j , j 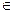 {1,2}
{1,2}
a30 = b1 , a40 = b2 , a00 = c0 , B ={3,4}
Пусть основная задача линейного программирования (max F, Ω) имеет решение
R=(x1,x2. … xm+n). Предположим, что найден такой оператор L, который не изменяя R, позволит записать (max F, Ω) в виде (max F`, Ω`), то есть
L(max F, Ω) = (max F`, Ω`):
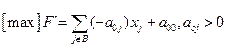
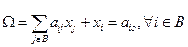
Тогда по внешнему виду этой задачи легко определить ее решение.
Действительно все коэффициенты при свободных переменных в F отрицательны.
Учитывая, что xj ≥ 0, увеличивая xj, мы не можем увеличить F`=a00 , следовательно
xj = 0 (j 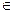 B), и тогда, анализируя Ω`, делаем вывод
B), и тогда, анализируя Ω`, делаем вывод
что xi = aio (i 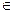 B)
B)
Пример:
| [max] F` – 20 = | 0*x1+0*x2-1*x3-1*x4+0*x5 0*x1+1*x2+1*x3-1*x4+0*x5 = 4 1*x1+0*x2-1*x3+2*x4+0*x5 = 4 0*x1+0*x2+0*x3-2*x4+1*x5 = 2 |
Здесь В={1,2,5}, следовательно,
x1=4,
x2=4,
x3=x4=0,
x5=2,
F`=20.
Оператор L позволяет записать (max F, Ω) в виде (max F`, Ω`) за несколько итераций, на каждой его действие сводится к эквивалентному преобразованию, заключающемуся в замене столбца коэффициентов, стоящих при одном из свободных переменных
(е-столбец) На столбец коэффициентов при одном из базисных переменных (s-столбец).
С геометрической точки зрения эти преобразования можно интерпретировать как переходы от одной вершины многогранника ограничений к другой, характеризующейся большим значением целевой функции.
В этом можно убедиться, если на каждой итерации вычислить решение
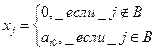
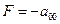
Указанные эквивалентные преобразования удобно проводить в специальной таблице, в j-том столбце которой записаны коэффициенты при 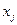 .
.
| e | S | ||||||
| γ | |||||||
| a01 | a02 | a00 | k | ||||
| a31 | a32 | a30 | 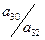
| ||||
| a41 | a42 | a40 | 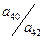
| S |
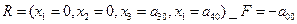
Предположим, что в целевой функции существуют положительные коэффициенты при свободных переменных. Выберем переменную с наибольшим положительным коэффициентом в целевой функции, то есть в “0”-ой строке таблицы.
Например если a02>a01, то е=2.
Таким образом е-столбец будем выбирать по правилу:
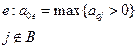
Введя в базис е, можно увеличить значение переменной xe, тем самым увеличив значение F. Переменную xe можно увеличивать до такого значения, чтобы не нарушить ни одного ограничения, поэтому целесообразно исследовать отношение 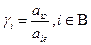 , и выбрать строку, которой соответствует наименьшее положительное
, и выбрать строку, которой соответствует наименьшее положительное 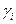 , то есть
, то есть
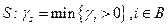
В нашем случае B={3,4}, 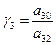 ,
, 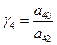 , пусть
, пусть 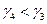 , тогда S=4. Элемент
, тогда S=4. Элемент 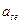 называют ведущим элементом.
называют ведущим элементом.
Чтобы поменять местами e и s столбцы, разделим s-строку на ведущий элемент и получим e-строку в новой (k+1) таблице:
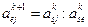
Таким образом на месте ведущего элемента будет стоять 1. Исключим 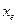 из целевой функции и остальных ограничений, для этого вычтем из оставшихся строк вновь полученную e-строку, умноженную предварительно на
из целевой функции и остальных ограничений, для этого вычтем из оставшихся строк вновь полученную e-строку, умноженную предварительно на 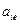 , получив в е-столбце нули на месте остальных элементов:
, получив в е-столбце нули на месте остальных элементов:
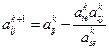
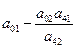
| 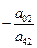
| 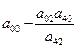
| |||
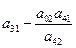
| 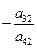
| 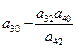
| |||
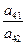
| 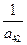
| 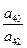
|
Обычно в симплекс-таблицах не записывают столбцы при базисных переменных.
Следовательно, L-оператор можно описать:
- Вычисляют решение R:
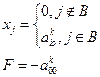
- Если все
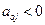 , то получено единственное оптимальное решение R.
, то получено единственное оптимальное решение R.
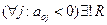
Если все 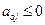 , то найдено одно из эквивалентных оптимальных решений R
, то найдено одно из эквивалентных оптимальных решений R
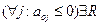
Если существует 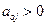 , то выбирают е-столбец и s-строку.
, то выбирают е-столбец и s-строку.
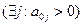
| 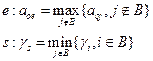
|
- Производят замену e-столбца и s-строки:
3.1 На месте ведущего элемента 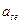 записывают его обратную величину:
записывают его обратную величину:
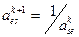
3.2 Строка, где находится ведущий элемент, делят на ведущий элемент:
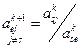
3.3 Столбец, где находится ведущий элемент, делят на ведущий элемент с обратным знаком:
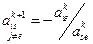
3.4 Вычтем из оставшихся строк вновь полученную е-строку, предварительно умноженную на элемент е-столбца вычисляемой строки.
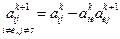
Дата публикования: 2015-07-22; Прочитано: 1115 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
