Обобщенный метод максимального правдоподобия

В обобщенном ММП предполагается, что ошибка модели подчиняется нормальному закону распределения с ковариационной матрицей W, определенной выражением либо (3.1), либо (3.4), т. е. j (e)~ N (0, W _e). В этом случае плотность нормального закона распределения значений ошибки e_t, t =1,2,... Т; можно представить в следующем виде:

j (e)= 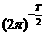½ W _e ½ 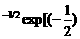× e ¢ W _y ^–1 e ]. (3.17)

Используя матрицу S _e, выражение (3.17) можно записать и так

j (e)= 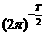(s ₁ s ₂... s_T)½ S _e ½ 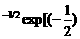× e ¢ S _e ^–1 e ], (3.18)

где в зависимости от предполагаемых свойств ошибки матрица S _e определена либо выражением (3.1), либо (3.4). При этом и в том и в другом случае предполагается, что s ₁ = s ₂=...= s_Т.

Заметим, что при независимых ошибках e ₁, e ₂, ..., e_Т

j (e)=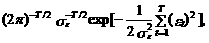

что совпадает с функцией максимального правдоподобия, определенной выражением (2.109).

Логарифм выражения (3.18), являющийся логарифмом функции правдоподобия для взаимозависимых или гетероскедастичных ошибок e ₁, ..., e_Т с учетом представления их вектора в виде e = у – Х × a, записывается следующим образом:

l =– 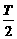ln(2 p) – 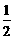ln½ W _e ½– 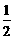(у – Х × a)¢ W _e ^–1(у – Х × a)=

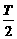=– ln(2 p) – 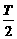ln s_e ² – 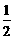ln½ S _e ½– 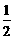(у – Х × a)¢ S _e ^–1(у – Х × a). (3.19)

Дифференцируя выражение (3.19) по вектору параметров a и дисперсии ошибки s_e ² и приравнивая нулю частные производные, получим

¶ l /¶ a = 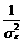(Х ¢ × S _e ^-1 × у + Х ¢ × S _e ^–1 × Х × a)=0;

¶ l /¶ s_e ²= 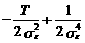(у – Х × a)¢× S _e ^–1 × (у – Х × a)=0. (3.20)

Из выражения (3.20) непосредственно получим выражения для оценок параметров модели и ее дисперсии в следующем виде:

a =(Х ¢ × S _e ^–1 × у)^–1 Х ¢ S _e ^–1 × у;

s_e ²= 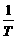(у – Х × a)¢× S _e ^–1 × (у – Х × a). (3.21)

Заметим, что с учетом равенства W _e = s ² S _e первое выражение из (3.21) можно записать в следующем виде:

a =(Х ¢ × W _e ^–1 × у)^–1 Х ¢ W _e ^–1 × у. (3.22)

Из сопоставления выражений (3.16) и (3.21), (3.14) и (3.22) непосредственно вытекает, что при “нормально” распределенных ошибках эконометрической модели при утрате их свойств независимости и гомоскедастичности обобщенные МНК и ММП определяют оценки коэффициентов этой модели по одним и тем же выражениям. При этом, как и в разделе 2.5, можно показать, что оценки ОММП обладают свойствами асимптотической несмещенности, состоятельности и эффективности.

Основные проблемы, связанные с применением обобщенного МНК для оценки коэффициентов эконометрической модели, состоят в том, что априорно матрицы W и S являются неизвестными, поскольку определить численные значения их элементов можно только после того, как получены оценки коэффициентов модели a ₀, a ₁,... a_n. Разрешить это противоречие можно на основе ряда подходов, которые будут рассмотрены в последующих параграфах данной главы.