Линейные функции и их свойства

Пусть 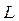– класс всех линейных функций.

Определение. называется линейной функцией, если её представление в виде полинома Жегалкина содержит только линейные члены, то есть

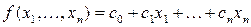, (8)

где 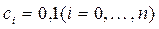; существенные переменные входят с коэффициентом 1, фиктивные – с коэффициентом 0.

1) Очевидно, что класс 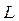замкнут, так как линейное выражение, составленное из линейных выражений, является линейным.

2) Функции ;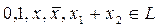

3) Функции ;

4) 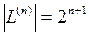, так как выбор констант 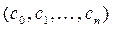в представлении (8) осуществляется именно 2ⁿ⁺¹ способами.

Докажем леммы о нелинейной функции.

Лемма 1. Если 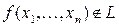, то из неё путем подстановки констант 0 и 1 можно получить нелинейную функцию, зависящую от двух переменных.

Доказательство: Из теоремы 6 известно, что любая функция из может быть представлена в виде полинома Жегалкина, причем единственным образом.

Рассмотрим 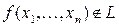. Так как – нелинейная, то её разложение в виде полинома содержит нелинейные слагаемые.

Пусть 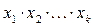– конъюнкция в полиноме Жегалкина, содержащая наименьшее число переменных. При этом 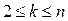. Делаем следующую подстановку констант:

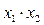– оставляем,

,

.

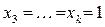В результате мы получили, что 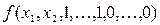есть нелинейная функция, конъюнкция переходит в 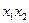. Так как – конъюнкция, содержащая наименьшее число переменных, то остальные конъюнкции обратятся в 0. Лемма доказана.

Лемма 2. Из нелинейной функции от 2-х переменных подстановкой функций вида 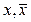можно получить либо конъюнкцию 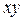, либо функцию вида .

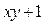Доказательство: Любая нелинейная функция от 2-х переменных 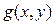может быть представлена в виде:

.

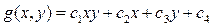Так как 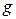– нелинейная, то 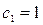; так как
; .

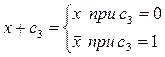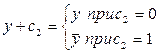Тогда

.

;

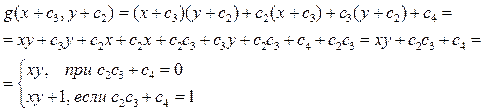
Лемма доказана.