Задание № 11

Составить уравнения касательной плоскости и нормали к поверхности S в точке М ₀(х ₀, у ₀, z ₀). Записать нормальный вектор к поверхности S в точке М ₀(х ₀, у ₀, z ₀).

11.1. S: x ² + y ² + z ² + 6 z – 4 x + 8 = 0, M ₀(2, 1, –1).

11.2. S: x ² + z ² – 4 y ² = –2 xy, M ₀(–2, 1, 2).

11.3. S: x ² + y ² + z ² + 3 z – xy = 7, M ₀(1, 2, 1).

11.4. S: x ² + y ² + z ² + 6 y + 4 x = 8, M ₀(–1, 1, 2).

11.5. S: 2 x ² – y ² + z ² – 4 z + y = 13, M ₀(2, 1, –1).

11.6. S: x ² + y ² + z ² – 6 y + 4 z + 4 = 0, M ₀(2, 1, –1).

11.7. S: x ² + z ² – 5 yz + 3 y = 46, M ₀(1, 2, –3).

11.8. S: x ² + y ² – xz – yz = 0, M ₀(0, 2, 2).

11.9. S: x ² + y ² + 2 yz – z ² – y – 2 z = 2, M ₀(1, 1, 1).

11.10. S: x ² + y ² – z ² – 2 xz + 2 x – z = 0, M ₀(1, 1, 1).

11.11. S: z = x ² + y ² – 2 xy + 2 x – y, M ₀(–1, –1, –1).

11.12. S: z = – x ² + y ² + 2 xy – 3 y, M ₀(1, –1, 1).

11.13. S: z = x ² – y ² – 2 xy – x – 2 y, M ₀(–1, 1, 1).

11.14. S: x ² – 2 y ² + z ² + xz – 4 y – 13 = 0, M ₀(3, 1, 2).

11.15. S: 4 y ² – z ² + 4 xy – xz + 3 z = 9, M ₀(1, –2, 1).

11.16. S: z = x ² + y ² – 3 xy – x + y + 2, M ₀(2, 1, 0).

11.17. S: 2 x ² – y ² + 2 z ² + xy + xz = 3, M ₀(1, 2, 1).

11.18. S: x ² – y ² + z ² – 4 х + 2 y = 14, M ₀(3, 1, 4).

11.19. S: x ² + y ² – z ² + xz + 4 у = 4, M ₀(1, 1, 2).

11.20. S: x ² – y ² – z ² + xz + 4 x = –5, M ₀(–2, 1, 0).

11.21. S: x ² + y ² – xz + yz – 3 x = 11, M ₀(1, 4, –1).

11.22. S: x ² + 2 y ² + z ² – 4 xz = 8, M ₀(0, 2, 0).

11.23. S: x ² – y ² – 2 z ² – 2 y = 0, M ₀(–1, –1, 1).

11.24. S: x ² + y ² – 3 z ² + xy = –2 z, M ₀(1, 0, 1).

11.25. S: 2 x ² – y ² + z ² – 6 x + 2 y = –6, M ₀(1, –1, 1).

11.26. S: x ² + y ² – z ² + 6 xy – z = 8, M ₀(1, 1, 0).

11.27. S: z = 2 x ² – 3 y ² + 4 x – 2 y + 10, M ₀(–1, 1, 3).

11.28. S: z = x ² + y ² – 4 xy + 3 x – 15, M ₀(–1, 3, 4).

11.29. S: z = x ² + 2 y ² + 4 xy – 5 y – 10, M ₀(–7, 1, 8).

11.30. S: z = 2 x ² – 3 y ² + xy + 3 x + 1, M ₀(1, –2, 2).

Решение задач типового варианта контрольной работы № 4

2 Задание № 6. Дана функция 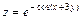. Показать, что F= 0, где .

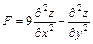Решение. Вычислим ; :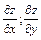

;

;

.

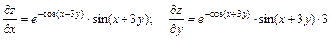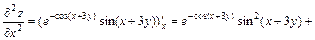
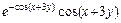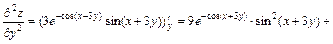
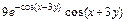Тогда

.

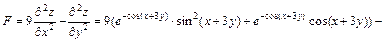
Ответ: 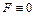, что и требовалось доказать. v

2 Задание № 7. Даны функция z = x ² + 2 xy - 3 y ² и точка M (1,97; 0,99). С помощью полного дифференциала вычислить приближенное значение функции z = f (x, y) в данной точке. Вычислить точное значение функции в точке M ₀(2; 1) и оценить относительную погрешность вычислений.

Решение. Найдем частные производные и полный дифференциал данной функции в любой точке (х, у)

, .

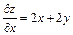Тогда полный дифференциал .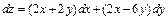

Вычислим dz в точке М ₀(2, 1) при приращениях

dx =D x = х – х ₀ = 1,97 - 2 = -0,03, dy»D y = у – у ₀ = 0,99 - 1 = -0,01,

dz = (2×2 + 2×1)(-0,03) + (2×2 - 6×1)(0,01) = -0,18 + 0,02 = -0,16.

Найдем z (M ₀) = 2² + 2×2×1 - 3×1² = 5.

Тогда 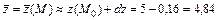– приближенное значение функции в точке М.

Вычислим точное значение функции z в точке М

z = 1,97² + 2×1,97×0,99 - 3×0,99² = 3,8809 + 3,9006 - 2,9403 = 4,8412.

Найдем относительную погрешность

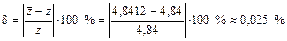
Ответ: Приближенное значение ,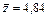

относительная погрешность 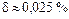. v

2 Задание 8. Дана функция z = 3 x ² - 5 xy + 7 y; точка А (2, 1) и вектор 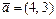. Найти а) 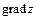в точке А и его численное значение; б) производную в точке А по направлению вектора .

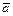Решение. а) По определению градиента .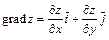

Значение градиента в точке А определяется по формуле

.

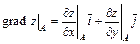Найдем частные производные в точке А

; .

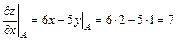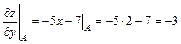Следовательно, 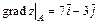, 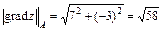– численное значение .

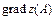б) Производную от функции z по направлению вектора 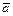в точке А определим из соотношения

,

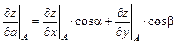где cosα и cos β – направляющие косинусы данного вектора 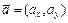, которые вычисляются по формулам 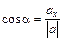; ; 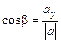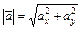. Тогда , ; ,

.

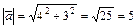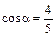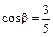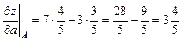Ответ: 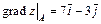; ; 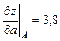. v

2 Задание 9. Найти наибольшее и наименьшее значения функции

z = х ²+ 4 ху – у ² – 6 х – 2 у

в области D: x ³ 0, y ³ 0; 2 x + 3 y – 6 £ 0. Выполнить чертеж области D.

Решение. 1. Найдем критические точки функции z = х ²+ 4 ху – у ² – 6 х – 2 у:

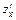= 2 х + 4 у – 6; 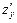= 4 х – 2 у – 2.

Решим систему уравнений

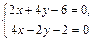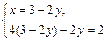Þ Þ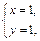

и получим одну стационарную точку (1; 1), которая лежит внутри заданной области (рис. 6).

2. Найдем наибольшее и наименьшее значения z = f (x, у)на границе области, которую составляют отрезок ОА оси Ох 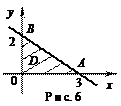; отрезок OВ оси Оу; отрезок AB прямой.

На отрезке ОА: у = 0; 0 £ х £ 3

z = f (x,0)= х ² – 6 х

(непрерывная функция одной переменной). Из уравнения 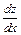= 0, т. е.

2 х – 6 = 0,

имеем х = 3 (критическая точка, не являющаяся внутренней).

На отрезке OB: х = 0, 0 £ y £ 2

z = f (0, у) = – у ² –2 у.

Из уравнения 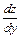= 0, т. е.

– 2 у – 2 = 0,

имеем у = –1; эта точка лежит вне отрезка [0, 2] и поэтому нас не интересует.

На отрезке АВ имеем

х = 3 – 1,5 у; 0 £ у £ 2,

z = –9 + 10 y – 19 у ² /4, 0 £ у £ 2.

Из уравнения 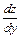= 0, т. е. 10 – 19 y / 2 = 0, найдем у = 20 / 19, что дает z (20 / 19) = –71 / 19.

3. В точках стыка участков граница имеем следующие значения f (x, у):

f (О) = f (0,0) = 0; f (В) = f (0,2) = –8; f (А) = f (3,0) = –9.

4. Сравнивая между собой вычисленные значения f (x, у), т. е. числа –4, –71 / 19, 0, –8, –9, приходим к заключению, что свое набольшее значение в данном замкнутом треугольнике функция принимает в точке О (0; 0), наименьшее – в точке А (3, 0), при этом z _наиб = z (0; 0) = 0; z _наим = z (3; 0) = –9.

Ответ: z _наиб = z (0; 0) = 0; z _наим = z (3; 0) = –9. v

2 Задание 10. Экспериментально получены пять значений искомой функции y = f (x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f (x) в виде y = ax + b.

xi
yi	0,5		1,5

Решение. Составим систему

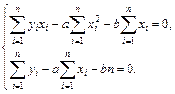(1)

Для этого предварительно вычислим суммы

; ;

; .

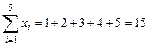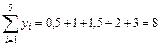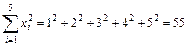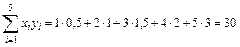Подставим полученные значения в систему (1)

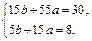
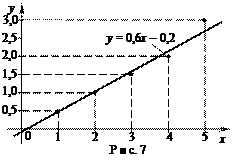Умножим второе уравнение на (-3) и сложим с первым, тогда

10 а = 6 Þ а = 0,6.

Подставим значение а = 0,6 во второе уравнение и получим

5 b + 9 = 8; b = -0,2.

Следовательно, наилучшее приближение представляется формулой

y = ax + b = 0,6 x - 0,2.

Построим график этой зависимости и нанесем на него экспериментальные точки (рис. 7).

Ответ: y = 0,6 x - 0,2. v

2 Задание 11.1. Составить уравнения касательной плоскости и нормали к поверхности 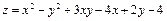в точке М ₀(–1; 0; 1). Записать нормальный вектор к поверхности в точке М ₀.

Решение. Поверхность задана явно z = f (x, y). Тогда уравнение касательной плоскости имеет вид

;

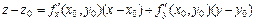уравнения нормали – ;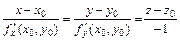

нормальный вектор к поверхности в точке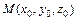

.

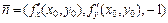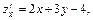
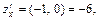
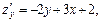
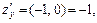
z – 1 = –6(x + 1) – y Þ 6 x + y + z + 5 = 0 – уравнение касательной плоскости; 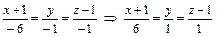– уравнения нормали; – нормальный вектор к поверхности в точке M ₀.

Ответ: 6 x + y + z + 5 = 0 – уравнение касательной плоскости; 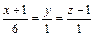– уравнения нормали; . v

2 Задание 11.2. Составить уравнения касательной плоскости и нормали к поверхности 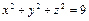в точке M ₀(2, –2, 1). Записать нормальный вектор к поверхности в точке M ₀.

Решение. Поверхность задана неявно уравнением 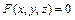, где 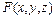= x ² + y ² + z ² – 9. Тогда уравнение касательной плоскости имеет вид

;

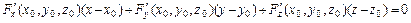уравнения нормали – ;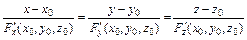

нормальный вектор к поверхности в точке –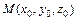

.

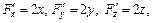
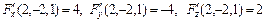Þ

4(x – 2) – 4(y + 2) + 2(z – 1) = 0 Þ 2 x – 2 y + z – 9 = 0 – уравнение касательной плоскости;

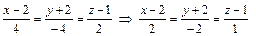– уравнения нормали; 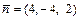– нормальный вектор к поверхности в точке M ₀.

Ответ: 2 x – 2 y + z – 9 = 0 – уравнение касательной плоскости; 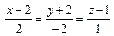– уравнения нормали; 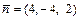– нормальный вектор.

Замечание. Решение задачи задания 11.1 сводится к решению по схеме решения задачи 11.2, если уравнение поверхности z = f (x, y) переписать в виде 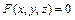: f (x, y) – z = 0. v