П.1. Алгебраическая лемма

Условимся о некоторых определениях и обозначениях.

Определение 5.1. Пусть матрица получена путем вычеркивания из матрицы некоторых строк и столбцов. Тогда матрицу будем называть подматрицей матрицы и записывать это обстоятельство в виде .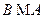

Пусть матрица имеет 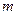строк и 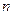столбцов, ,

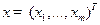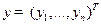
и 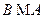. Если у вектора 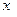(соответственно 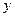) вычеркнуть координаты с номерами, совпадающими с номерами строк (столбцов), вычеркнутых из при построении подматрицы , то получившийся вектор будем обозначать через ().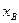

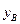Следующая лемма имеет алгебраический характер, т.е. справедлива для любых, а не только для платежных матриц.

Лемма 5.1. Пусть в матрице размерности 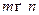и ранга 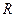первые 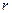строк и первые 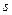столбцов линейно независимы, 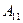– подматрица матрицы , стоящая на пересечении указанных строк и столбцов. Тогда существует такая квадратная невырожденная подматрица ранга 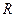, что .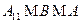

Доказательство. Очевидно 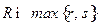.Дополним первые 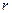строк матрицы другими строками так, чтобы их число стало равным 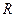, и они в совокупности были линейно независимыми. Это возможно сделать, т.к. ранг матрицы равен 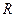. Для простоты рассуждений будем считать, что выбранная совокупность строк образована первыми 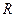строками матрицы . Аналогичные операцию и соглашение осуществим и со столбцами матрицы . Убедимся, что подматрица, стоящая на пересечении первых 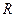строк и столбцов, которую обозначим через , является невырожденной. Это утверждение требует доказательства, несмотря на то, что у матрицы первые 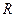строк и столбцов линейно независимы. При построении подматрицы эти же строки и столбцы могут стать укороченными и в этом случае стать линейно зависимыми. Доказывая лемму от противного, допустим, что строки матрицы линейно зависимы. Тогда одна из них за счет линейного комбинирования других строк может быть превращена в нулевую. Пусть таковой оказалась первая строка матрицы . Поскольку у матрицы первые 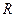строк и столбцов линейно независимы, то в первой строке матрицы после такого комбинирования останется, по крайней мере, один ненулевой элемент. Пусть такой элемент остался в 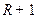столбце. Отметим, что поскольку первые 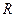столбцов матрицы линейно независимы, то в подматрице, состоящей из этих столбцов, есть минор порядка 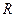, отличный от нуля. Следовательно, в подматрице, составленной из первых 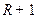столбцов матрицы , найдется отличный от нуля минор

порядка 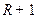. Но это противоречит тому, что ранг матрицы равен 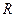. Значит, предположение о том, что строки матрицы линейно зависимы не справедливо. Теорема доказана.