 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Некоторые сведения о последовательностях
|
|
Пусть каждому значению 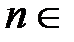 N поставлено в соответствие (по определённым правилам) определённое действительное число
N поставлено в соответствие (по определённым правилам) определённое действительное число 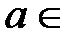 R; тогда множество упорядоченных действительных чисел
R; тогда множество упорядоченных действительных чисел  называется числовой последовательностью и обозначается
называется числовой последовательностью и обозначается 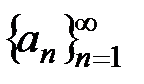 , где
, где 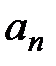 − общий член последовательности. Например, последовательность
− общий член последовательности. Например, последовательность 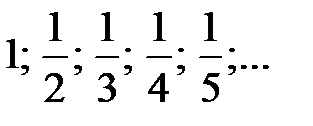 имеет общий член
имеет общий член 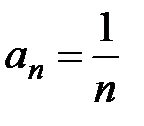 , где
, где 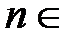 N.
N.
Определение 1. Последовательность 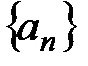 называется убывающей, если
называется убывающей, если 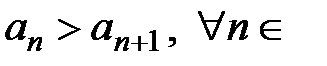 N, и возрастающей, если
N, и возрастающей, если 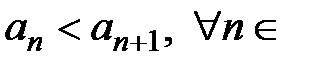 N.
N.
Определение 2. Последовательность 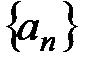 называется ограниченной сверху, если существует такое число М,
называется ограниченной сверху, если существует такое число М, 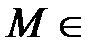 R, что
R, что 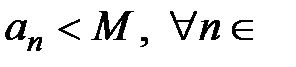 N, и ограниченной снизу, если существует такое число М,
N, и ограниченной снизу, если существует такое число М, 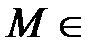 R, что
R, что 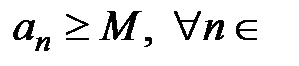 N.
N.
Определение 3. Последовательность 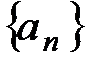 называется ограниченной, если она ограничена как снизу, так и сверху, т.е. существует такое число М > 0
называется ограниченной, если она ограничена как снизу, так и сверху, т.е. существует такое число М > 0
(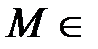 R), что
R), что 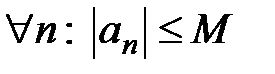 .
.
Определение 4. Число а называется пределом последовательности 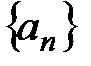 ,
,
если для любого сколь угодно малого положительного числа 
найдётся такой номер 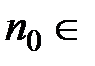 N, зависящий от
N, зависящий от  , что для всех натуральных чисел
, что для всех натуральных чисел 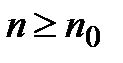 выполняется неравенство
выполняется неравенство 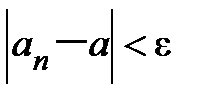 . Тогда
. Тогда 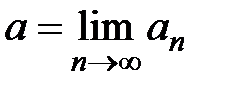 означает,
означает,
что 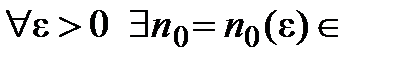 N такое, что для всех
N такое, что для всех 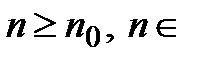 N:
N: 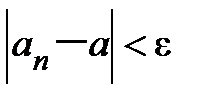 . При
. При
этом говорят, что последовательность  сходится к числу а.
сходится к числу а.
Приведём некоторые свойства сходящихся последовательностей.
–Если последовательность имеет предел, то он единственен.
–Если последовательность имеет конечный предел, то эта последовательность ограничена.
–Если последовательность возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел.
–Если последовательность возрастает (убывает) и не ограничена сверху (снизу), то она имеет бесконечный предел + ¥ (− ¥).
1.2. Числовой ряд. Основные понятия теории числовых рядов:
сходимость, расходимость, сумма ряда. Примеры
Пусть задана бесконечная последовательность чисел 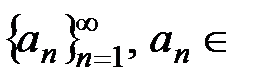 R.
R.
Определение 5. Бесконечным числовым рядом называется выражение вида 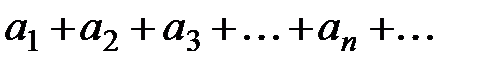 , обозначаемое как
, обозначаемое как 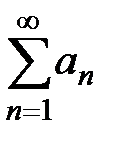 . Числа
. Числа 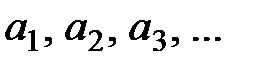 называются членами (элементами) числового ряда.
называются членами (элементами) числового ряда.
Определение 6. Сумма первых n членов ряда называется n-й частичной суммой ряда: 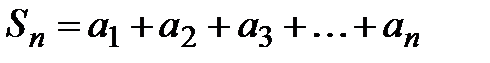 .Тогда
.Тогда 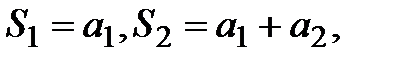
 и т.д. Получаем последовательность частичных сумм
и т.д. Получаем последовательность частичных сумм 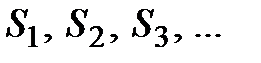 :
: 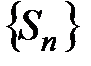 .
.
Таким образом, каждому числовому ряду 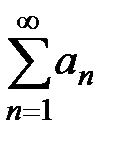 можно поставить в соответствие последовательность частичных сумм
можно поставить в соответствие последовательность частичных сумм 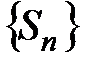 :
: 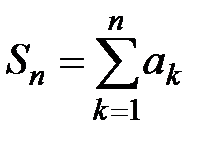 .
.
Определение 7. Если существует конечный или бесконечный предел S
последовательности частичных сумм 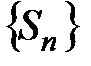 , то он называется суммой ряда
, то он называется суммой ряда 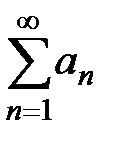 , т.е.
, т.е. 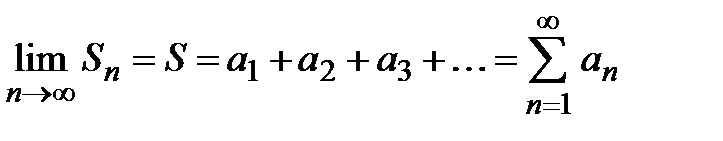 .
.
Если S конечно (S < ¥), то ряд называется сходящимся; если S = ¥ или S не существует, то ряд называется расходящимся и суммы ряд не имеет.
Итак, если дан ряд, то всегда можно поставить вопрос, сходится ли он (иными словами, существует ли конечный предел 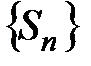 ) или расходится?
) или расходится?
Приведём примеры исследования ряда на сходимость и нахождения его суммы.
Пример 1. Исследовать на сходимость ряд 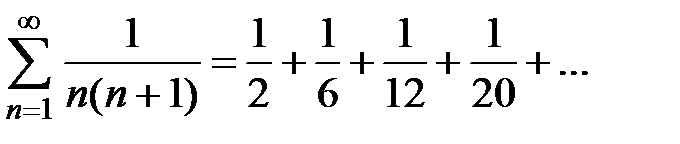 и найти его сумму.
и найти его сумму.
Решение. Обозначим  − общий член ряда. Тогда частичная сумма ряда
− общий член ряда. Тогда частичная сумма ряда 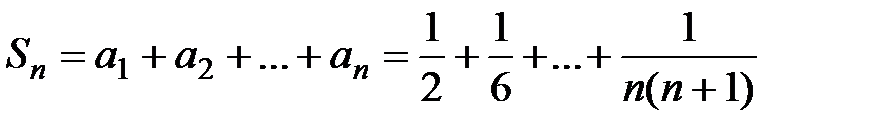 . Так как
. Так как 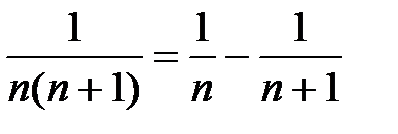 , то
, то 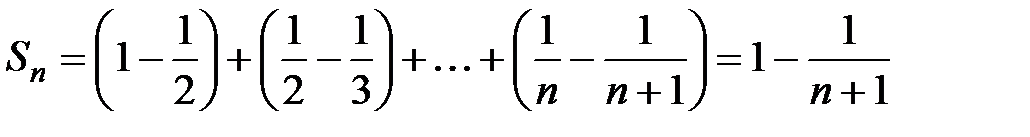 . Тогда
. Тогда  , т.е. ряд сходится и его сумма S = 1.
, т.е. ряд сходится и его сумма S = 1.
Пример 2. Исследовать на сходимость ряд 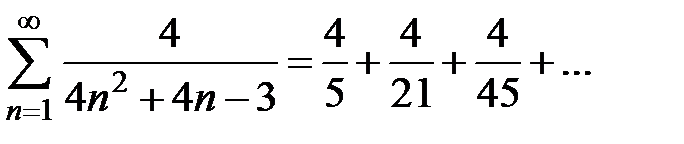 и найти его сумму.
и найти его сумму.
Решение. Обозначим 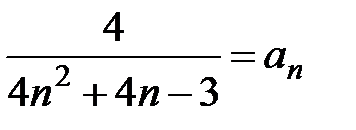 − общий член ряда. Тогда,
− общий член ряда. Тогда,
частичная сумма ряда 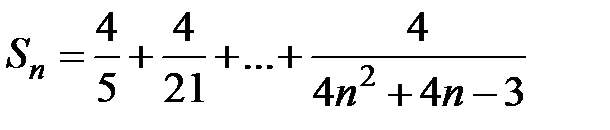 . Так как
. Так как
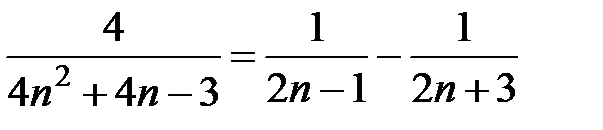 , то
, то
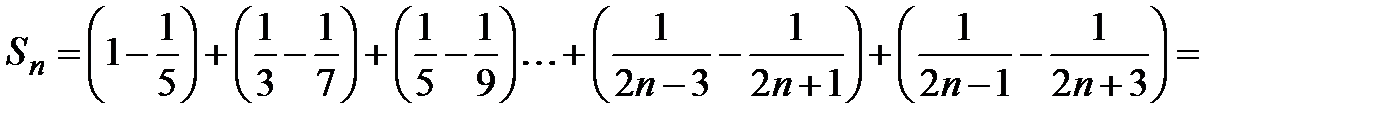
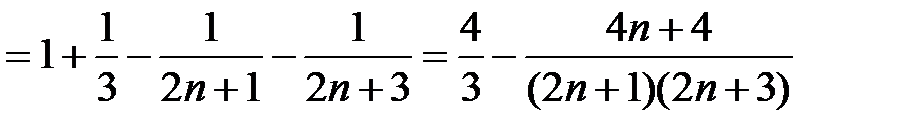 , тогда
, тогда 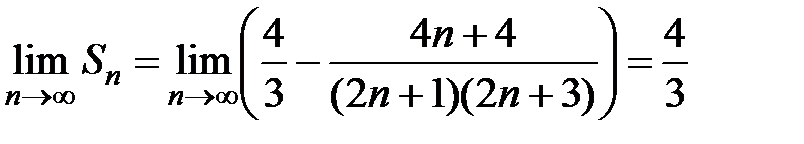 , т.е. ряд сходится и его сумма
, т.е. ряд сходится и его сумма 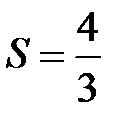 .
.
Пример 3. Исследовать на сходимость ряд 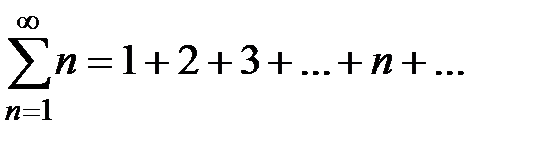 .
.
Решение. Обозначим общий член ряда 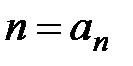 . Тогда, частичная сумма ряда
. Тогда, частичная сумма ряда 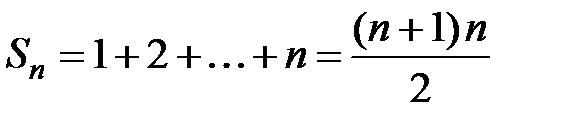 ,
, 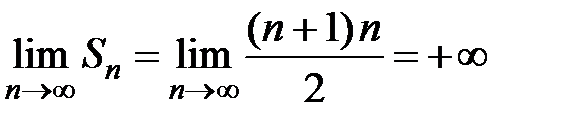 , т.е. сумма ряда
, т.е. сумма ряда 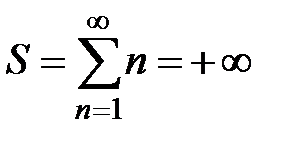 и ряд расходится.
и ряд расходится.
Пример 4. Исследовать на сходимость ряд, составленный из членов геометрической прогрессии.
Решение. Пусть дана геометрическая прогрессия 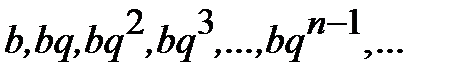 , где q − знаменатель прогрессии. Ряд
, где q − знаменатель прогрессии. Ряд 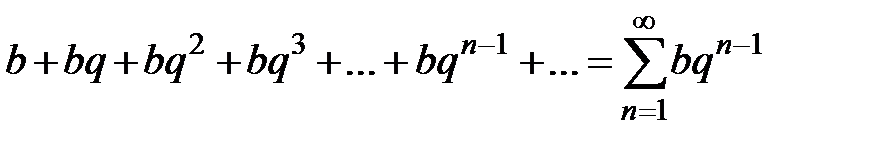 называется рядом геометрической прогрессии. Обозначим
называется рядом геометрической прогрессии. Обозначим 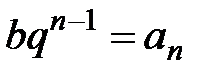 − общий член ряда. При
− общий член ряда. При 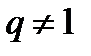 n - частичная сумма этого ряда равна
n - частичная сумма этого ряда равна
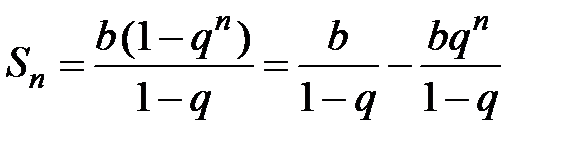 .
.
Рассмотрим частные случаи.
–Если  , то
, то 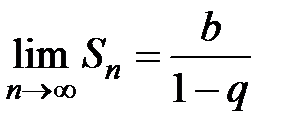 , т.е. ряд сходится.
, т.е. ряд сходится.
–Если 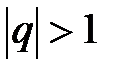 , то
, то 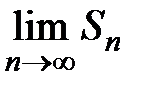 не существует, т.е. последовательность
не существует, т.е. последовательность 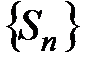
расходится, а значит расходится и исследуемый ряд геометрической
прогрессии.
–При 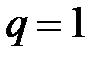 ряд имеет вид
ряд имеет вид 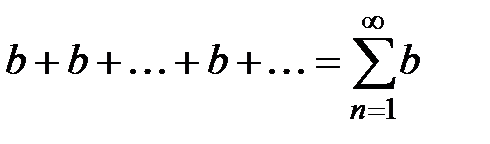 . Тогда
. Тогда 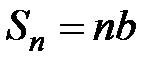 ,
,  , т.е. ряд расходится.
, т.е. ряд расходится.
–При 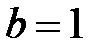 ,
,  ряд имеет вид
ряд имеет вид 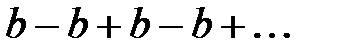 , тогда
, тогда 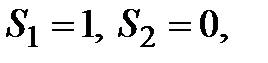
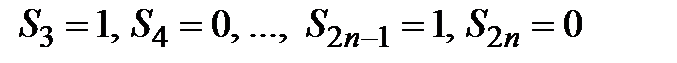 , т.е. предела последовательности
, т.е. предела последовательности 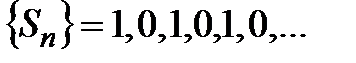 не существует, а значит, искомый ряд расходится.
не существует, а значит, искомый ряд расходится.
Таким образом, ряд геометрической прогрессии сходится тогда и только тогда, когда 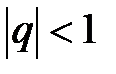 , в остальных случаях ряд расходится.
, в остальных случаях ряд расходится.
1.3. Основные свойства сходящихся рядов,
необходимый признак сходимости
Пусть дан числовой ряд 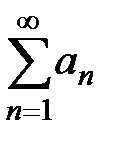 . Сформулируем его основные свойства.
. Сформулируем его основные свойства.
Свойство 1. Если сходится ряд, полученный из данного ряда отбрасыванием или присоединением конечного числа членов, то сходится и сам данный ряд, и наоборот. Иными словами, отбрасывание или
присоединение конечного числа членов ряда не влияет на сходимость ряда.
Доказательство. Пусть 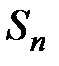 – частичная сумма ряда
– частичная сумма ряда 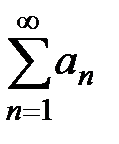 ,
, 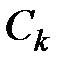 – сумма
– сумма 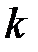 отброшенных членов и
отброшенных членов и 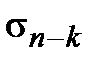 – сумма членов ряда, входящих в сумму
– сумма членов ряда, входящих в сумму 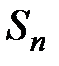 и не входящих в сумму Ck. При достаточно большом n все отброшенные члены будут содержаться в сумме
и не входящих в сумму Ck. При достаточно большом n все отброшенные члены будут содержаться в сумме 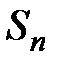 , т.е.
, т.е. 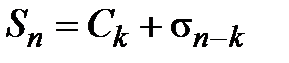 (k – фиксированное число,
(k – фиксированное число,  – const). Тогда, если существует
– const). Тогда, если существует 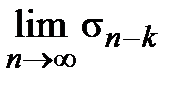 , то существует и
, то существует и 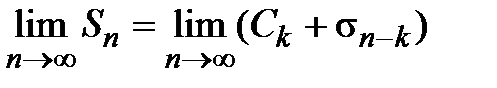 , т.е. исходный ряд
, т.е. исходный ряд 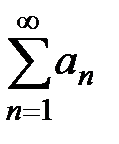 сходится. И наоборот, если существует
сходится. И наоборот, если существует 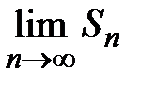 , то существует и
, то существует и 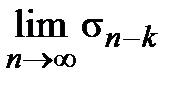 , т.е. сходится составленный ряд. Аналогично доказывается сходимость при добавлении к ряду
, т.е. сходится составленный ряд. Аналогично доказывается сходимость при добавлении к ряду 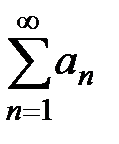 конечного числа членов.
конечного числа членов.
Свойство 2. Если сходится ряд  , то ряд
, то ряд 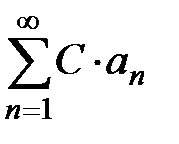 (С – константа) также сходится, причём его сумма равна
(С – константа) также сходится, причём его сумма равна 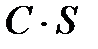 .
.
Доказательство. Пусть  – частичная сумма ряда
– частичная сумма ряда 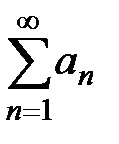 ,
, 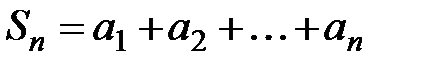 , и
, и  − частичная сумма ряда
− частичная сумма ряда 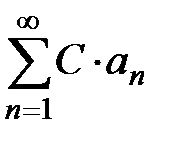 ,
, 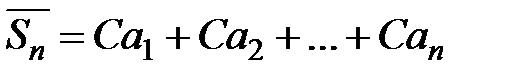 . Тогда
. Тогда 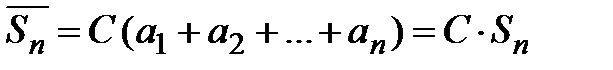 .
.
Отсюда, если существует 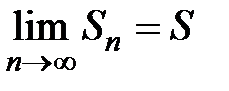 (ряд
(ряд  сходится), то существует
сходится), то существует 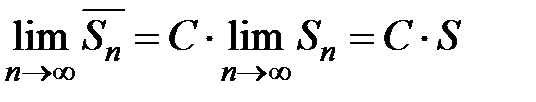 , т.е. ряд
, т.е. ряд 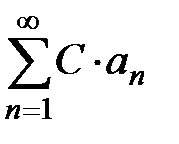 также сходится.
также сходится.
Свойство 3. Если ряды 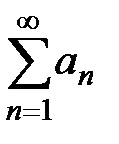 и
и  сходятся и их суммы равны A и B соответственно, то их можно почленно складывать (или вычитать), причём ряды
сходятся и их суммы равны A и B соответственно, то их можно почленно складывать (или вычитать), причём ряды 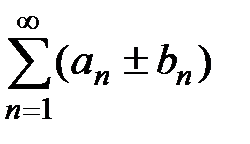 также сходятся и их суммы равны
также сходятся и их суммы равны 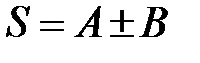 .
.
Доказательство. Пусть 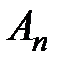 ,
, 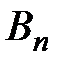 и
и 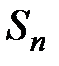 – частичные суммы этих рядов, тогда
– частичные суммы этих рядов, тогда 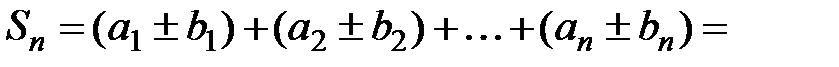
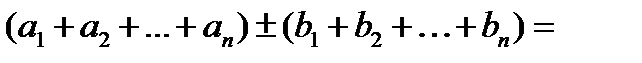
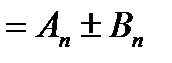 . Переходя к пределу при
. Переходя к пределу при 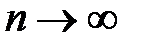 , получим
, получим 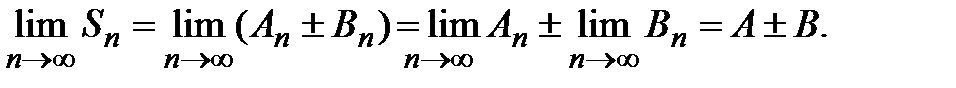
Теорема 1 (необходимый признак сходимости рядов). Пусть ряд 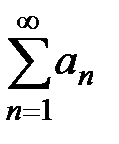
сходится, тогда его общий член  стремится к 0 (при
стремится к 0 (при 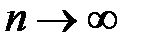 )
) 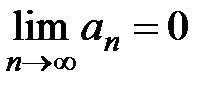
(обратное не всегда верно).
Доказательство. Так как ряд 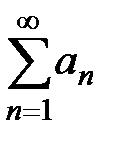 сходится и его сумма равна S, то для его частичных сумм
сходится и его сумма равна S, то для его частичных сумм 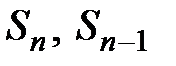 имеют место равенства
имеют место равенства 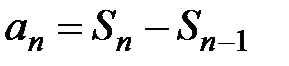 ;
; 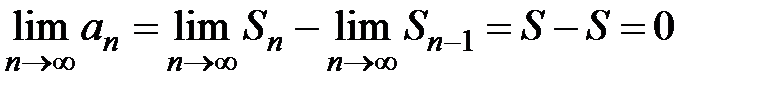 . Что и требовалось доказать.
. Что и требовалось доказать.
Условие сходимости, сформулированное в теореме 1, является необходимым, но не достаточным, т.е. при выполнении условия 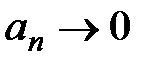 ряд может расходиться. Рассмотрим пример такого ряда:
ряд может расходиться. Рассмотрим пример такого ряда: 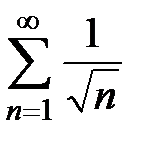 , где
, где 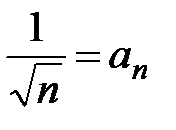 − общий член ряда. Тогда
− общий член ряда. Тогда 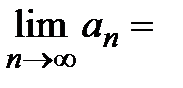
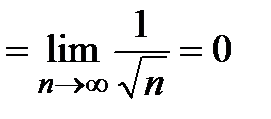 . Частичная сумма ряда имеет вид
. Частичная сумма ряда имеет вид 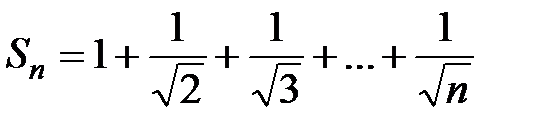 . Очевидно, каждый член этой суммы
. Очевидно, каждый член этой суммы 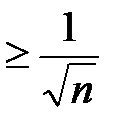 , тогда оценка
, тогда оценка 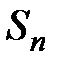 даёт неравенство:
даёт неравенство: 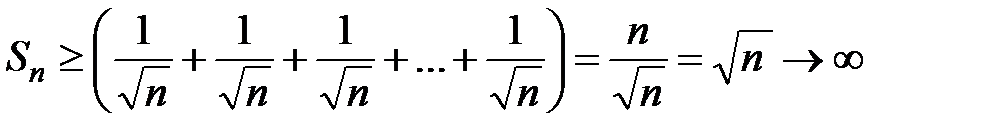 , следовательно,
, следовательно,  , т.е. исходный ряд расходится, хотя
, т.е. исходный ряд расходится, хотя 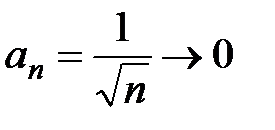 .
.
Следствие из теоремы 1. Если общий член ряда аn (при 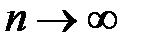 ) не стремится к 0, то ряд
) не стремится к 0, то ряд 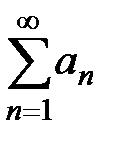 расходится (достаточный признак расходимости ряда).
расходится (достаточный признак расходимости ряда).
Пример 5. Исследовать на сходимость ряд  .
.
Решение. Обозначим общий член ряда 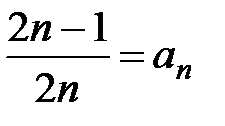 . Так как
. Так как 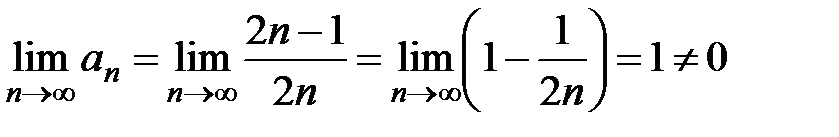 , то из следствия теоремы 1
, то из следствия теоремы 1
следует, что ряд расходится.
Пример 6. Исследовать на сходимость ряд 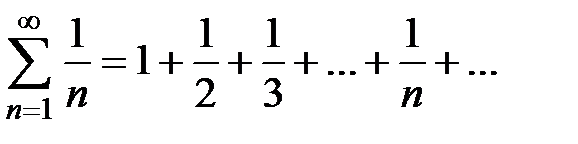
Решение. Общий член ряда имеет вид 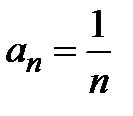 . Данный ряд называется гармоническим, так как каждый его член равен среднему гармоническому двух соседних:
. Данный ряд называется гармоническим, так как каждый его член равен среднему гармоническому двух соседних: 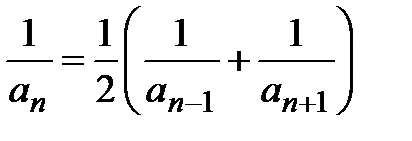 . Очевидно неравенство:
. Очевидно неравенство: 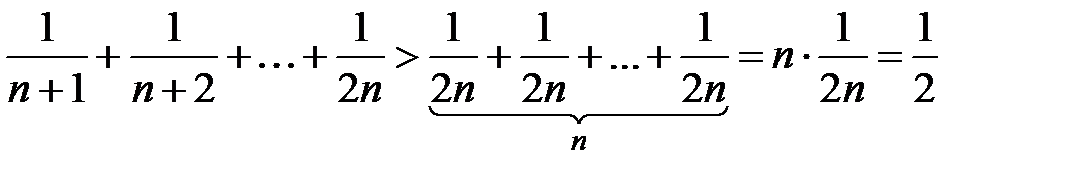 . Члены гармонического ряда, начиная с третьего, объединим в группы по 2, 4, 8, 16, …, 2 k -1 членов в каждой группе. Очевидно, сумма каждой группы можно оценить следующим образом:
. Члены гармонического ряда, начиная с третьего, объединим в группы по 2, 4, 8, 16, …, 2 k -1 членов в каждой группе. Очевидно, сумма каждой группы можно оценить следующим образом: 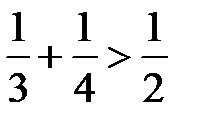 ;
; 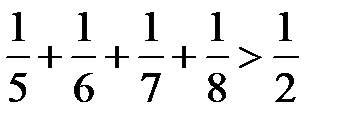 ;
; 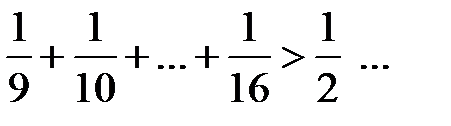 , т.е.
, т.е.
каждая из этих сумм в отдельности больше 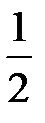 . Таким образом, для частичных сумм с номерами
. Таким образом, для частичных сумм с номерами 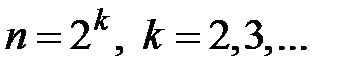 выполняются неравенства:
выполняются неравенства: 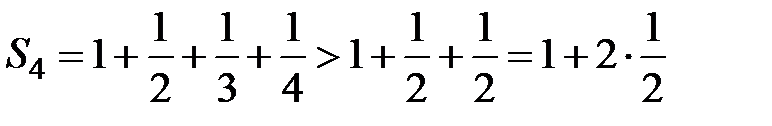 ,
,
 , …,
, …,
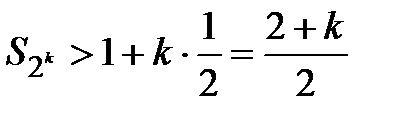 ,т.е. частичные суммы гармонического ряда неограниченно растут с увеличением
,т.е. частичные суммы гармонического ряда неограниченно растут с увеличением 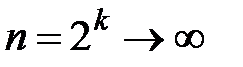 при
при 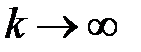 , значит,
, значит, 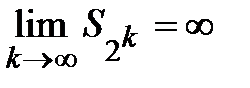 . Получаем, что гармонический ряд
. Получаем, что гармонический ряд  расходится.
расходится.
Дата публикования: 2014-10-20; Прочитано: 619 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
