 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лекция 4. Функциональные ряды. Степенные ряды. Формула Тейлора
|
|
4.1. Функциональные ряды: основные понятия, область сходимости
Определение 1. Ряд, члены которого являются функциями одной или
нескольких независимых переменных, определёнными на некотором множестве, называется функциональным рядом.
Рассмотрим функциональный ряд 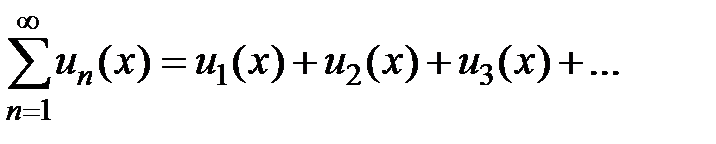 , члены которого являются функциями одной независимой переменной х. Сумма первых n членов ряда
, члены которого являются функциями одной независимой переменной х. Сумма первых n членов ряда 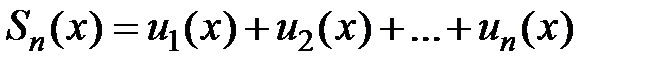 является частичной суммой данного функционального ряда. Общий член
является частичной суммой данного функционального ряда. Общий член 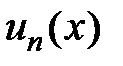 есть функция от х, определённая в некоторой области. Рассмотрим функциональный ряд в точке
есть функция от х, определённая в некоторой области. Рассмотрим функциональный ряд в точке 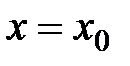 . Если соответствующий числовой ряд
. Если соответствующий числовой ряд 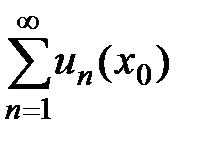 сходится, т.е. существует предел частичных сумм этого ряда
сходится, т.е. существует предел частичных сумм этого ряда 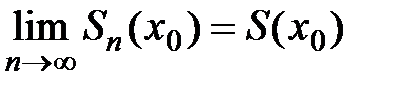 (где
(где 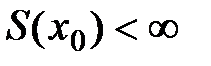 − сумма числового ряда), то точка
− сумма числового ряда), то точка 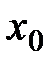 называется точкой сходимости функционального ряда
называется точкой сходимости функционального ряда 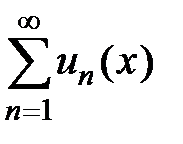 . Если числовой ряд
. Если числовой ряд 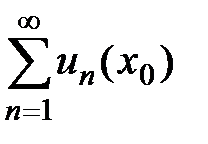 расходится, то точка
расходится, то точка 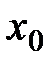 называется точкой расходимости функционального ряда.
называется точкой расходимости функционального ряда.
Определение 2. Областью сходимости функционального ряда 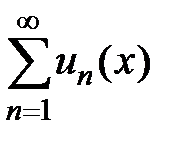 называется множество всех таких значений х, при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается
называется множество всех таких значений х, при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается 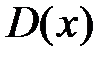 . Отметим, что
. Отметим, что 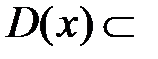 R.
R.
Функциональный ряд сходится в области 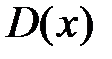 , если для любого
, если для любого 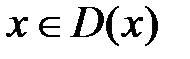 он сходится как числовой ряд, при этом его сумма будет некоторой функцией
он сходится как числовой ряд, при этом его сумма будет некоторой функцией 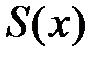 . Это так называемая предельная функция последовательности
. Это так называемая предельная функция последовательности 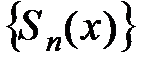 :
: 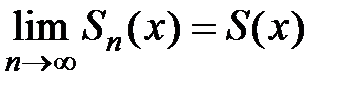 .
.
Как находить область сходимости функционального ряда 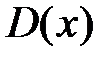 ? Можно использовать признак, аналогичный признаку Даламбера. Для ряда
? Можно использовать признак, аналогичный признаку Даламбера. Для ряда 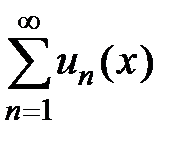 составляем
составляем 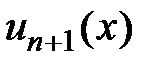 и рассматриваем предел при фиксированном х:
и рассматриваем предел при фиксированном х: 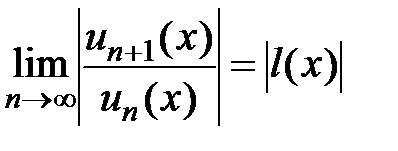 . Тогда
. Тогда 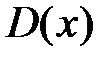 является решением неравенства
является решением неравенства 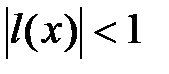 и решением уравнения
и решением уравнения 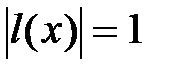 (берём только те решения уравнения, в
(берём только те решения уравнения, в
которых соответствующие числовые ряды сходятся).
Пример 1. Найти область сходимости ряда 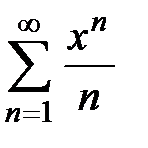 .
.
Решение. Обозначим 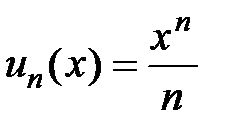 ,
, 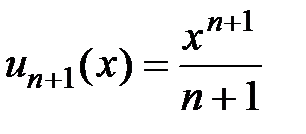 . Составим и вычислим предел
. Составим и вычислим предел 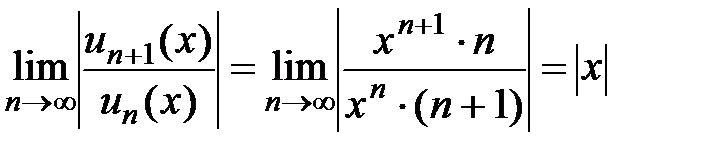 , тогда область сходимости ряда определяется неравенством
, тогда область сходимости ряда определяется неравенством 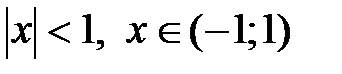 и уравнением
и уравнением 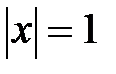 . Исследуем дополнительно сходимость исходного ряда в точках, являющимися корнями уравнения:
. Исследуем дополнительно сходимость исходного ряда в точках, являющимися корнями уравнения:
а) если 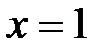 ,
, 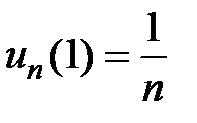 , то получается расходящийся ряд
, то получается расходящийся ряд 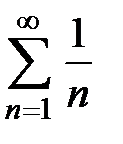 ;
;
б) если 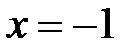 ,
, 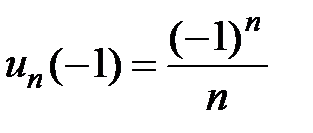 , то ряд
, то ряд 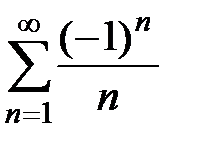 сходится условно (по
сходится условно (по
признаку Лейбница, пример 1, лекция 3, разд. 3.1).
Таким образом, область сходимости 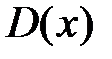 ряда
ряда 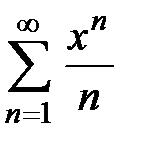 имеет вид:
имеет вид: 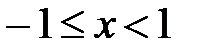 .
.
4.2. Степенные ряды: основные понятия, теорема Абеля
Рассмотрим частный случай функционального ряда, так называемый степенной ряд 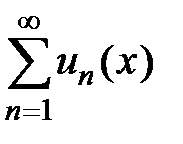 , где
, где 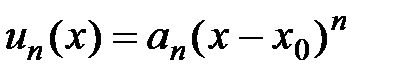 .
.
Определение 3. Степенным рядом называется функциональный ряд вида 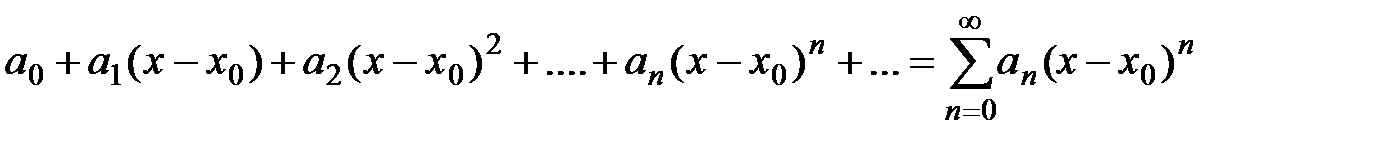 ,
,
где 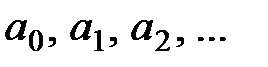 − постоянные числа, называемые коэффициентами ряда.
− постоянные числа, называемые коэффициентами ряда.
Степенной ряд есть «бесконечный многочлен», расположенный по возрастающим степеням 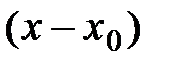 . Любой числовой ряд
. Любой числовой ряд 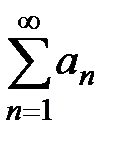 является
является
частным случаем степенного ряда при 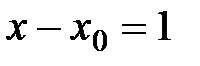 .
.
Рассмотрим частный случай степенного ряда при 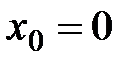 :
: 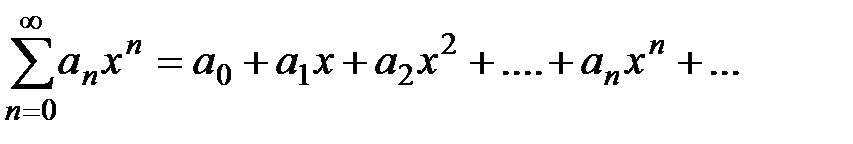 . Выясним, какой вид имеет
. Выясним, какой вид имеет
область сходимости данного ряда 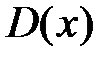 .
.
Теорема 1 (теорема Абеля). 1) Если степенной ряд 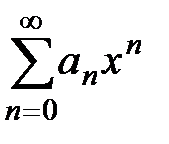 сходится в точке
сходится в точке 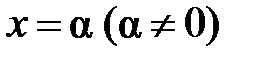 , то он абсолютно сходится при всяком х, для которого справедливо неравенство
, то он абсолютно сходится при всяком х, для которого справедливо неравенство 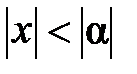 .
.
2) Если же степенной ряд расходится при 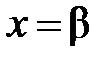 , то он расходится при всяком х, для которого
, то он расходится при всяком х, для которого 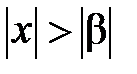 .
.
Доказательство. 1) По условию степенной ряд сходится в точке 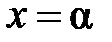 ,
,
т. е. сходится числовой ряд
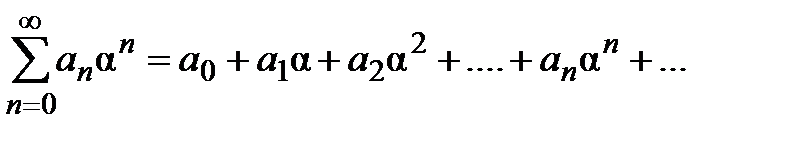 (1)
(1)
и по необходимому признаку сходимости его общий член стремится к 0, т.е. 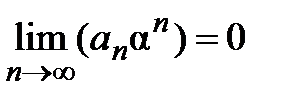 . Следовательно, существует такое число
. Следовательно, существует такое число 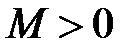 , что все члены ряда ограничены этим числом:
, что все члены ряда ограничены этим числом: 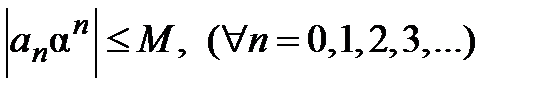 .
.
Рассмотрим теперь любое х, для которого 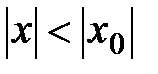 , и составим ряд из абсолютных величин:
, и составим ряд из абсолютных величин: 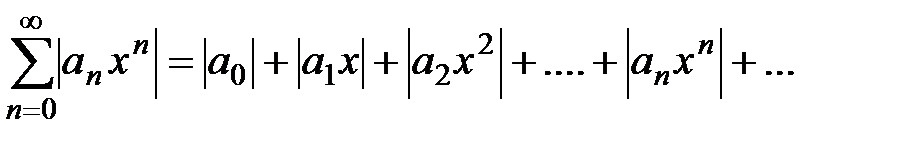 .
.
Запишем этот ряд в другом виде: так как 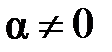 , то
, то 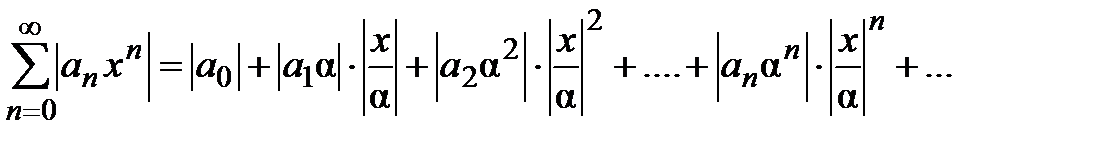 (2).
(2).
Из неравенства 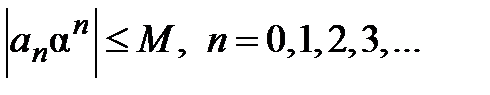 получаем
получаем 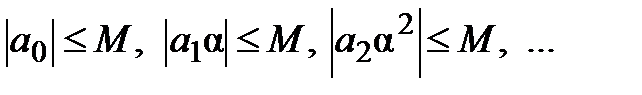 , т.е. ряд
, т.е. ряд
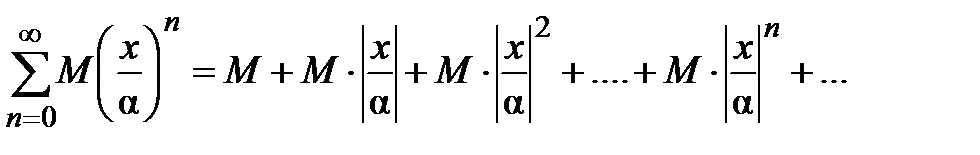 (3)
(3)
состоит из членов, которые больше соответствующих членов ряда (2). Ряд 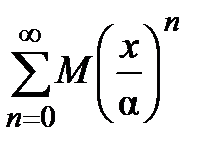 представляет собой сходящийся ряд геометрической прогрессии со знаменателем
представляет собой сходящийся ряд геометрической прогрессии со знаменателем 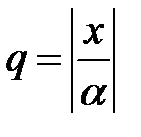 , причём
, причём 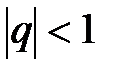 , так как
, так как 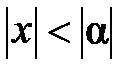 . Следовательно, ряд (2) сходится при
. Следовательно, ряд (2) сходится при 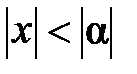 . Таким образом, степенной ряд
. Таким образом, степенной ряд 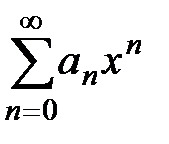 абсолютно сходится.
абсолютно сходится.
2) Пусть ряд 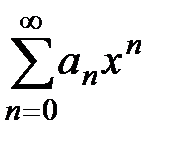 расходится при
расходится при 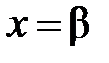 , иными словами,
, иными словами,
расходится числовой ряд 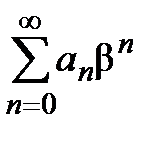 . Докажем, что для любого х (
. Докажем, что для любого х (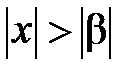 ) ряд расходится. Доказательство ведётся от противного. Пусть при некотором
) ряд расходится. Доказательство ведётся от противного. Пусть при некотором
фиксированном 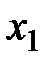 (
(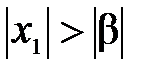 ) ряд сходится, тогда он сходится при всех
) ряд сходится, тогда он сходится при всех 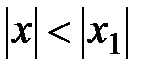 (см. первую часть данной теоремы), в частности, при
(см. первую часть данной теоремы), в частности, при 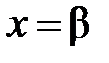 , что противоречит условию 2) теоремы 1. Теорема доказана.
, что противоречит условию 2) теоремы 1. Теорема доказана.
Следствие. Теорема Абеля позволяет судить о расположении точки сходимости степенного ряда. Если точка 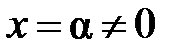 является точкой сходимости степенного ряда, то интервал
является точкой сходимости степенного ряда, то интервал 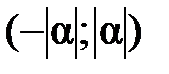 заполнен точками сходимости; если точкой расходимости является точка
заполнен точками сходимости; если точкой расходимости является точка 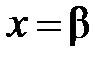 , то
, то
бесконечные интервалы 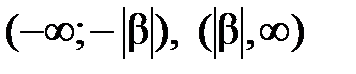 заполнены точками расходимости (рис. 1).
заполнены точками расходимости (рис. 1).

Рис. 1. Интервалы сходимости и расходимости ряда
Можно показать, что существует такое число 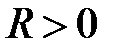 , что при всех
, что при всех 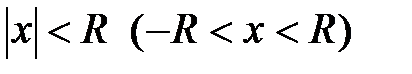 степенной ряд
степенной ряд 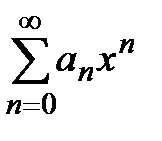 абсолютно сходится, а при
абсолютно сходится, а при 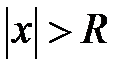 − расходится. Будем считать, что если ряд сходится только в одной точке 0, то
− расходится. Будем считать, что если ряд сходится только в одной точке 0, то 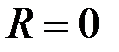 , а если ряд сходится при всех
, а если ряд сходится при всех 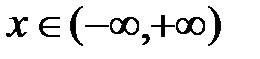 , то
, то 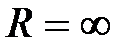 .
.
Определение 4. Интервалом сходимости степенного ряда 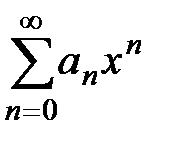 называется такой интервал
называется такой интервал 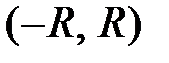 , что при всех
, что при всех 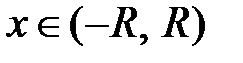 этот ряд сходится и притом абсолютно, а для всех х, лежащих вне этого интервала, ряд расходится. Число R называется радиусом сходимости степенного ряда.
этот ряд сходится и притом абсолютно, а для всех х, лежащих вне этого интервала, ряд расходится. Число R называется радиусом сходимости степенного ряда.
Замечание. На концах интервала 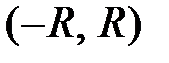 вопрос о сходимости или расходимости степенного ряда решается отдельно для каждого конкретного ряда.
вопрос о сходимости или расходимости степенного ряда решается отдельно для каждого конкретного ряда.
Покажем один из способов определения интервала и радиуса сходимости степенного ряда.
Рассмотрим степенной ряд 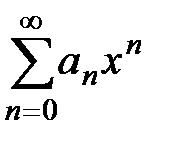 и обозначим
и обозначим 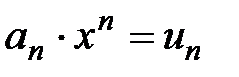 .
.
Составим ряд из абсолютных величин его членов:
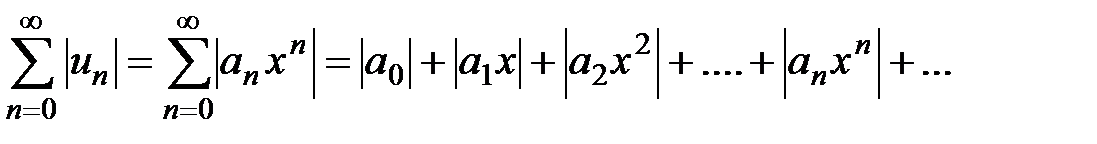
и применим к нему признак Даламбера.
Пусть существует
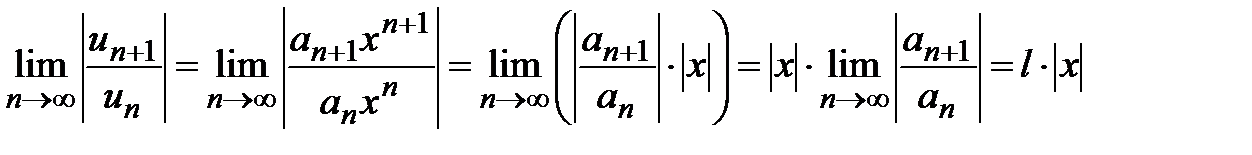 ,
,
где
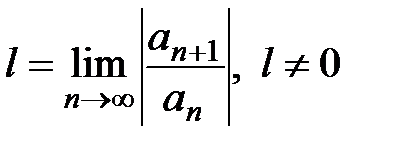 .
.
По признаку Даламбера ряд сходится, если 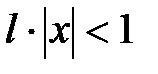 , и расходится, если
, и расходится, если 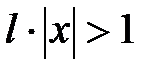 . Отсюда ряд сходится при
. Отсюда ряд сходится при 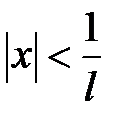 , тогда интервал сходимости:
, тогда интервал сходимости: 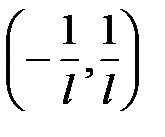 . При
. При 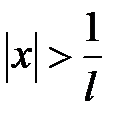 ряд расходится, так как
ряд расходится, так как 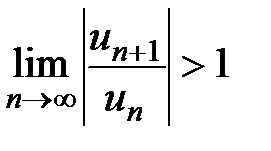 .
.
Используя обозначение 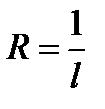 , получим формулу для определения радиуса сходимости степенного ряда:
, получим формулу для определения радиуса сходимости степенного ряда:
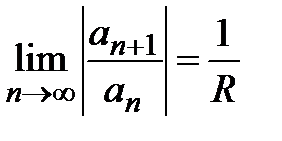 ,
,
где 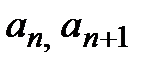 − коэффициенты степенного ряда.
− коэффициенты степенного ряда.
Если окажется, что предел 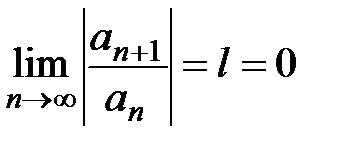 , то полагаем
, то полагаем 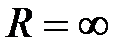 .
.
Для определения интервала и радиуса сходимости степенного ряда также можно использовать радикальный признак Коши, радиус сходимости ряда определяется из соотношения 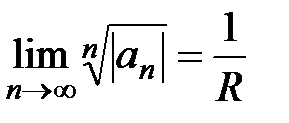 .
.
Определение 5. Обобщенным степенным рядом называется ряд вида
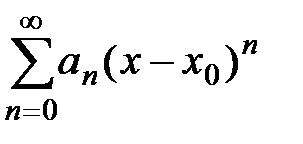 . Его также называют рядом по степеням
. Его также называют рядом по степеням 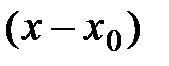 .
.
Для такого ряда интервал сходимости имеет вид: 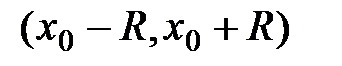 , где
, где 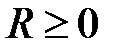 − радиус сходимости.
− радиус сходимости.
Покажем, как находится радиус сходимости для обобщенного степенного ряда.
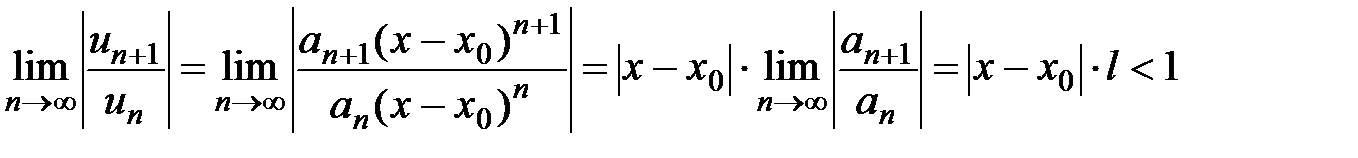 ,
,
т.е. 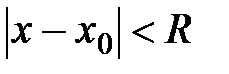 , где
, где 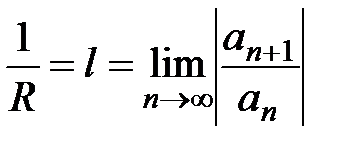 .
.
Если 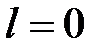 , то
, то 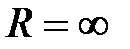 , и область сходимости
, и область сходимости 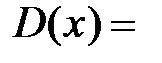 R; если
R; если 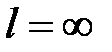 , то
, то 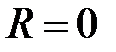 и область сходимости
и область сходимости 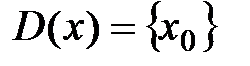 .
.
Пример 2. Найти область сходимости ряда 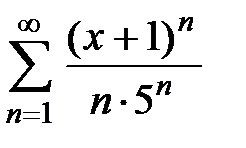 .
.
Решение. Обозначим 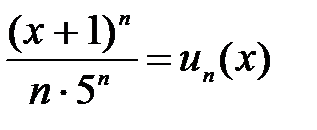 . Составим предел
. Составим предел
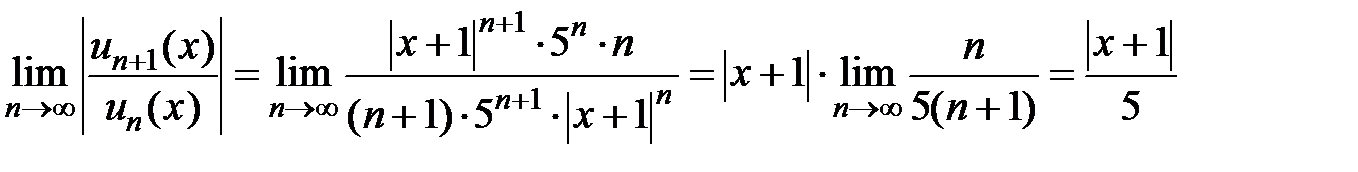 .
.
Решаем неравенство: 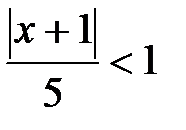 ,
, 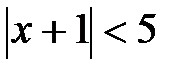 , следовательно, интервал
, следовательно, интервал
сходимости имеет вид: 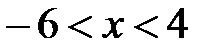 , причём R = 5. Дополнительно исследуем концы интервала сходимости:
, причём R = 5. Дополнительно исследуем концы интервала сходимости:
а) 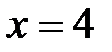 ,
, 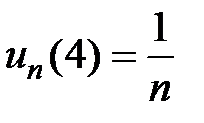 , получаем ряд
, получаем ряд 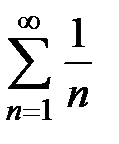 , который расходится;
, который расходится;
б) 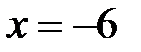 ,
, 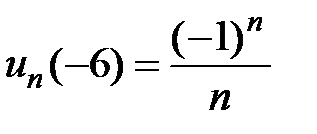 , получаем ряд
, получаем ряд 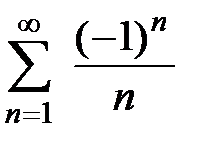 , который сходится
, который сходится
условно. Таким образом, область сходимости: 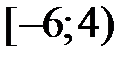 ,
, 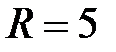 .
.
Ответ: область сходимости 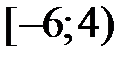 .
.
Пример 3. Ряд 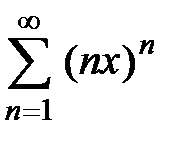 расходится для всех
расходится для всех 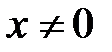 , так как
, так как 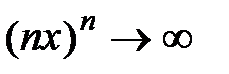 при
при 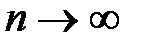 , радиус сходимости
, радиус сходимости 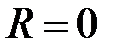 .
.
Пример 4. Ряд 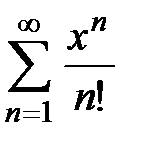 сходится при всех
сходится при всех 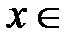 R, радиус сходимости
R, радиус сходимости 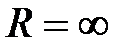 .
.
Дата публикования: 2014-10-20; Прочитано: 944 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
