 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Многошаговые методы решения задачи Коши. Постановка задачи
|
|
59. Методы предиктор – корректор для решения задачи Коши.
60. Методы предиктор – корректор для решения ДУ на основе метода Адамса.
1.Этапы решения задач на ЭВМ:
Реальные инженерные и физические задачи во всех областях науки и техники обычно решаются посредством использования двух подходов:
– физического эксперимента;
– предварительного анализа конструкций, схем, явлений с целью выбора каких-то их оптимальных параметров.
Первый подход связан с большими и не всегда оправданными затратами материальных и временных ресурсов.
Второй подход связан с математическим моделированием, в основе которого заложены знания фундаментальных законов природы и построение на их основе математических моделей для произвольных технических и научных задач.
Математические модели представляют собой упрощенное описание исследуемого явления с помощью математических символов и операций над ними. Математические модели разрабатываются с соблюдением корректности и адекватности по отношению к реальным процессам, но, как правило, с учетом простоты их технической реализации.
Практика показывает, что возникающие и истребованные технические решения во многом однозначны, что определяет ограниченное число существенно полезных математических моделей, извлекаемых из стандартного справочника «Курс высшей математики». К примеру, из арсенала этих моделей можно назвать такие как линейные и нелинейные уравнения, системы линейных и нелинейных уравнений, дифференциальные уравнения (ДУ), разновидности интегралов, функциональные зависимости, «целевые» функции для решения задач оптимизации и др.
При математическом моделировании важным моментом является первоначальная математическая постановка задачи. Она предполагает описание математической модели и указания цели ее исследования. Для одной и той же математической модели могут быть сформулированы и решены различные математические задачи. Например, для наиболее распространенной модели, такой как функциональная зависимость y = f (x) могут быть сформулированы следующие математические задачи:
1) найти экстремальное значение функции f (x): max f (x) или min f (x);
2) найти значение x, при котором f (x) = 0;
3) найти значение производной f ' (x), значение интеграла и т.д.
Бурное развитие вычислительной техники выдвинуло на передний план при решении практических инженерных и научных задач вычислительную математику и программирование.
Вычислительная математика изучает построение и исследование численных методов решения математических задач посредством реализации соответствующих математических моделей.
Программирование обеспечивает техническую реализацию их.
Обобщенную схему математического моделирования можно представить следующим образом:
2.Схема решения инженерных задач на ЭВМ:
Решение задачи на компьютере включает в себя следующие основные этапы, часть из которых осуществляется без участия компьютера,
1. Постановка задачи, разработка математической модели.
Решение задачи, особенно достаточно сложной - достаточно трудное дело, требующее много времени. И если задача выбрана неудачно, то это может привести к потере времени и разочарованию в применении ЭВМ для принятия решений. Каким же основным требованиям должна удовлетворять задача?
а. Должно существовать как минимум один вариант ее решения, ведь если вариантов решения нет, значит выбирать не из чего.
б. Надо четко знать, в каком смысле искомое решение должно быть наилучшим, ведь если, мы не знаем чего хотим, ЭВМ помочь нам выбрать наилучшее решение не сможет.
Выбор задачи завершается ее содержательной постановкой.
На этом этапе, на основе словесной формулировки задачи исследования выбираются переменные, подлежащие определению, записываются ограничения, связи с переменными в совокупности образующие математическую задачу решаемой проблемы. В результате инженерная задача приобретает вид формализованной математической задачи.
2. Выбор численного метода решения.
Для поставленной математической задачи необходимо выбрать метод ее численного решения, сводящий решение к последовательности арифметических и логических операций.
3. Разработка алгоритма и структуры данных.
Алгоритм - это конечный набор правил, позволяющих чисто механически решать любую конкретную задачу из некоторого класса однотипных задач. При этом подразумевается:
а. - исходные данные могут изменяться в определенных пределах: {массовость алгоритма}
б. - процесс применения правил к исходным данным (путь решения задачи) определен однозначно: {детерминированность алгоритма}
в. - на каждом шаге процесса применения правил известно, что считать результатом этого процесса: {результативность алгоритма}
Если модель описывает зависимость между исходными данными и искомыми величинами, то алгоритм представляет собой последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам.
Если выбранный для решения задачи численный метод реализован в виде стандартных библиотечных подпрограмм, то алгоритм обычно сводится описанию и вводу исходных данных. Более характерен случай, когда стандартные программы решают лишь часть задачи. Если и задача сложная, то не нужно решать все проблемы. Сложившийся в настоящее время к разработке сложных программ состоит в последовательном использовании принципов проектирования сверху вниз, модульного, структурного и объектно - ориентированного программирования. Четкая структуризация, разбиение ее на последовательные подзадачи, реализация подзадач отдельного модуля, постепенная детализация логики алгоритма, использование типовых логических конструкций.
4 Реализация алгоритма: Алгоритм записывают с помощью обычных математических символов. Для того чтобы он мог быть прочитан ЭВМ, необходимо составить программу. Программа - это описание алгоритма решения задачи, заданное на языке ЭВМ. Алгоритмы и программы объединяются понятием "математическое обеспечение". В настоящее время затраты на математическое обеспечение составляют примерно полторы стоимости ЭВМ, и постоянно происходит дальнейшее относительное удорожание математического обеспечения. Уже сегодня предметом приобретения является именно математическое обеспечение, а сама ЭВМ лишь тарой, упаковкой для него.
Далеко не для каждой задачи необходимо составлять индивидуальную программу. На сегодняшний день созданы мощные современные программные средства - пакеты прикладных программ (ППП).
Зачастую, к задаче можно подобрать готовый пакет, который прекрасно работает, решает многие задач, среди которых можно найти и наши. При таком подходе многие задачи будут решены достаточно быстро, ведь не надо заниматься программированием.
5. Подготовка задания, ввод, отладка и испытание программы. Прежде чем ввести исходные данные в ЭВМ, их, естественно, необходимо собрать. Причем не все имеющиеся на производстве исходные данные, как это часто пытаются делать, а лишь те, которые входят в задачу. Следовательно, сбор исходных данных не только целесообразно, но и необходимо производить лишь после того, как будет известна задача. Имея программу и вводя в ЭВМ исходные данные, мы получим решение задачи.
Программа вводится обычно с клавиатуры. При программировании и вводе данных с клавиатуры могут быть допущены ошибки. Их обнаружение, локализация и устранение выполняют на этапе отладки и тестирования, на это тратится 50-70% времени.
6. Реализация задачи на компьютере, обработка и оформление. К сожалению, достаточно часто математическое моделирование смешивают с одноразовым решением конкретной задачи с начальными, зачастую недостоверными данными. Для успешного управления сложными объектами необходимо постоянно перестраивать модель на ЭВМ, корректируя исходные данные с учетом изменившейся обстановки.
Нецелесообразно тратить время и средства на составление математической модели, чтобы по ней выполнить один единственный расчет. Математическая модель является прекрасным средством получения ответов на широкий круг вопросов, возникающих при планировании, проектировании и в ходе производства. Математическая модель может стать надежным помощником при принятии каждодневных решений, возникающих в ходе оперативного управления производством.
Решение задачи компьютер выдает на дисплей. Чтобы облегчить следующую работу, надо выводить решение задачи на экран с пояснениями.

3.Методы решения инженерных задач на ЭВМ:
Методы реализации математических моделей можно разделить на три группы:
1) графические;
2) аналитические;
3) численные.
Указанные методы используются как самостоятельно, так и совместно.
Графические методы позволяют оценивать порядок искомых величин и направление расчетных алгоритмов.
Аналитические методы (точные, приближенные) упрощают фрагментарные расчеты и позволяют успешно решать задачи оценки корректности и точности численных решений.
Основным инструментом реализации математических моделей являются численные методы, позволяющие свести решение задачи к вычислению конечного числа арифметических действий над числами и получение этого решения в виде числовых значений. Решение, получаемое численными методами, обычно является приближенным, т.е. содержит некоторую погрешность.
4.Погрешности численных решений и их источники. Оценка погрешностей:
Важнейшим моментом при математическом моделировании является обеспечение достоверности полученных решений. Но из практики известно, что лишь в редких случаях удается найти метод решения, приводящий к точному результату. Как правило, приближенные решения используются совместно с точными решениями, поэтому, наряду с выбором вычислительного метода, с точки зрения оптимальности алгоритма его реализации, важной задачей является оценка степени точности получаемого решения. Ее принято оценивать некоторой численной величиной, называемой погрешностью.
При решении любой практической задачи необходимо всегда указывать требуемую точность результата. В связи с этим необходимо уметь:
1) зная заданную точность исходных данных, оценивать точность результата (прямая задача теории погрешностей);
2) зная требуемую точность результата, выбирать необходимую точность исходных данных (обратная задача теории погрешностей).
На рассмотренных выше этапах математического моделирования имеют место следующие источники погрешностей:
1) погрешность математической модели;
2) погрешность исходных данных (неустранимая погрешность):
3) погрешность численного метода;
4) вычислительная погрешность.
Погрешность математической модели возникает из-за стремления обеспечить сравнительную простоту ее технической реализации и доступности исследования.
Нужно иметь в виду, что конкретная математическая модель (ММ), прекрасно работающая в одних условиях, может быть совершенно неприменима в других. С точки зрения потребителя, важным является правильная оценка области ее (ММ) применения.
Погрешность численного метода (погрешность аппроксимации), связана, например, с заменой интеграла суммой, с усечением рядов при вычислении функций, с интерполированием табличных значений функциональных зависимостей и т.п. Как правило, погрешность численного метода регулируема и может быть уменьшена до любого разумного значения путем изменения некоторого параметра.
Вычислительная погрешность возникает из-за округления чисел, промежуточных и окончательных результатов счета. Она зависит от правил и необходимости округления, а также от алгоритмов численного решения.
Вспомним технологию округления чисел.
1. Если старший отбрасываемый разряд меньше 5, то предшествующая ему цифра в числе не меняется.
2. Если старший отбрасываемый разряд больше 5, то предшествующая цифра в числе увеличивается на 1.
3. Если старший отбрасываемый разряд равен 5, то по общепринятому соглашению предшествующая ему четная цифра в числе не меняется (например, с = 3,965; с *» 3,96), а нечетная – увеличивается на единицу (например, с = 3,915; с *» 3,92).
4. При округлении целого числа отброшенные знаки не следует заменять нулями, надо применять умножение на соответствующие степени 10.
В основе процессов округления лежит идея минимальности разности значения с и его округления с *.
Пример 1. Округлить число с на соответствующее количество знаков:
1) с = 1,9396712; 2) с = 245,351365;
с *= 1,939671; с *= 245,35136;
с *= 1,93967; с *= 245,3514;
с *= 1,9397; с *= 245,351;
с *= 1,940; с *= 245,35;
с *= 1,94; с *= 245,4;
с *= 1,9; с *= 245;
с *= 2; с *= 2,4×102;
с *= 2×102;
Пример 2. Для обоснования необходимости применения округлений в целях экономии памяти приведем следующий пример. Задано выражение
S = 25,71×1,42 – 3,21×7,46 + 0,93×7,75 – 4,31×2,69.
1. Вычислить S точно:
S = 36,5082 – 23,9466 + 7,2075 – 11,5939 = 8,1752.
2. Вычислить S и округлить его до двух знаков после запятой:
S1* = 8,18.
3. Вычислить каждое произведение с двумя знаками после запятой и просуммировать:
S2* = 36,51 – 23,95 + 7,21 – 11,59 = 8,18.
5.Приближенные числа и оценка их погрешностей:
При численном решении задач приходится оперировать двумя видами чисел – точными и приближенными. К точным числам относятся числа, которые дают истинное значение исследуемой величины. К приближенным относятся числа, близкие к истинному значению, причем степень близости и определяется погрешностью вычислений.
Результатами вычислений являются, как правило, только приближенные числа. Поэтому для указания области неопределенности результата вводятся некоторые специальные понятия, широко используемые при подготовке исходных данных или (и) оценке погрешности численных решений.
Если х – точное, вообще говоря, неизвестное значение некоторой величины, а а – его приближение, то разность х – а называется ошибкой, или погрешностью приближения. Часто знак ошибки х – а неизвестен, поэтому используется так называемая абсолютная погрешность D(Х) приближенного числа а, определяемая равенством
D(Х) = | х – а |, (1)
откуда имеем х = а ± D(Х). (2)
Изучаемая числовая величина х именованная, т.е. определяется в соответствующих единицах измерения, например, в сантиметрах, килограммах и т.п. Погрешность (1) имеет ту же размерность.
Однако часто возникает необходимость заменить эту погрешность безразмерной величиной – относительной погрешностью. При этом из-за незнания точного значения изучаемой величины принято называть относительной погрешностью величину:
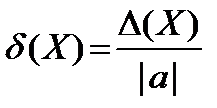
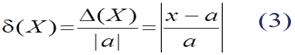
Относительную погрешность часто выражают в процентах: ×100%. Это погрешность на единицу измеряемой физической величины. Она сопоставима в идентичных экспериментах, т.е. характеризует качество измерения. А именно, точность результата лучше характеризуется его d(Х), так как абсолютная погрешность D(Х) не достаточна, к примеру, для характеристики качества измерения двух стержней l 1 = 100,8 см ± 0,1 см и l 2 = 5,2 см ± 0,1 см.
Очевидно, что качество измерения первого значительно выше.
В связи с тем, что точное значение х, как правило, неизвестно, то формулы (1)–(3) носят сугубо теоретический характер.
Для практических целей вводится понятие предельной погрешности. Предельная абсолютная погрешность D а – это верхняя оценка модуля абсолютной погрешности числа х, т.е.
| D х | £ D a.
При произвольном выборе, D а всегда стремятся каким-либо образом взять наименьшим.
Истинное значение числа х будет находиться в интервале с границами (а – D а) – с недостатком и (а + D а) – с избытком, т.е.
(а – D а) £ х £ (а + D а).
Условились для приближенных чисел по результатам округлений в качестве D а принимать единицу или 1/2 единицы оставленного разряда числа. Первое условие называют погрешностью в «широком» смысле, второе в «узком» смысле.
Пример для второго условия:
| а | 51,7 | –0,0031 | 16,00 | ||
| D а | 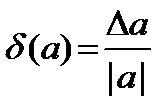 0,05 0,05
| 0,00005 | 0,5 | 0,005 |
Предельная относительная погрешность
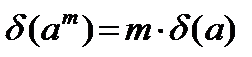
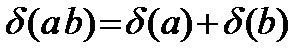

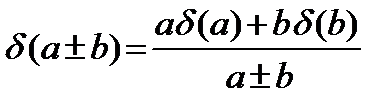 также может выражаться в процентах. При локальных ручных расчетах, и на этапе подготовки исходных данных существуют определенные правила оценки предельных погрешностей для арифметических операций (формулы – (4)):
также может выражаться в процентах. При локальных ручных расчетах, и на этапе подготовки исходных данных существуют определенные правила оценки предельных погрешностей для арифметических операций (формулы – (4)):
D(а ± D b) = D а + D b; D(а× b) = a× b [ d (а)+ d (b)] = b D а + a D b;
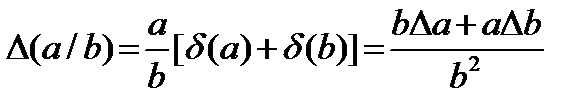
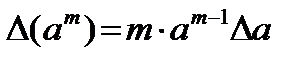
где D – предельная абсолютная погрешность; d – относительная предельная погрешность;
m – рациональное число.
6.Привила записи приближенных чисел. Понятия значащих и верных чисел:
Запись приближенных чисел должна подчиняться правилам, связанным с понятиями верных значащих цифр.
Любое десятичное число
х = ±a n a n– 1... a1 a0 a–1 a–2... a– m
представимо в виде
х = ±a n 10 n + a n– 110 n –1 +... a110 + a0 + a–110–1 + a–210–2 +... + a– m 10 –m,
где a i – цифры числа, 10 i – их позиция (± i).
Рассмотрим пример:
1358,7604 = 1×103 + 3×102 + 5×10 + 8 + 7×10–1 + 6×10–2 + 0×10–3 + 4×10–4.
Первая слева отличная от нуля цифра числа х и все расположенные справа от нее цифры называются значащими, т.е. числа 25,047 и –0,00250 имеют соответственно 5 и 3 значащих цифр. Последнее число может быть записано –2,50×10-3.
Значащая цифра a i называется верной (в узком смысле), если абсолютная погрешность числа не превосходит 1/2 единицы разряда, соответствующего этой цифре, т.е. D а £ 1/2×10 i, где 10 i указывает номер разряда (± i).
Пусть х * = 12,396 (х * приближение х) и известно D х * = 0,03. Согласно определению здесь:
D х * > 1/2×10–3; D х * > 1/2×10–2 и D х * < 1/2×10–1.
Значит, верными знаками будут 1, 2, 3, а 9 и 6 с омнительные.
Пусть х * = 0,037862 и D х * = 0,07. Здесь D х * > 1/2×10–1. Значит все значащие цифры сомнительные.
Если число записано с указанием его абсолютной погрешности
S = 20,7428; D S = 0,0926,
то число верных знаков можно отсчитывать от первой значащей цифры числа до первой значащей цифры его абсолютной погрешности. Здесь верные цифры 2, 0, 7.
Существуют определенные соглашения при оперировании понятиями верных значащих цифр.
1) Если число имеет лишь верные цифры, то и его округление имеет также только верные цифры.
2) Совпадение приближенного значения, имеющего все верные значащие цифры, с точным значением не обязательно.
3) Абсолютные и относительные погрешности числа принято округлять в большую сторону, так как при округлениях границы неопределенности числа, как правило, увеличиваются.
4) При изменении формы записи числа количество значащих цифр не должно меняться, т.е. необходимо соблюдать равносильность преобразований, например
7500 = 0,7500×104; 0,110×102 = 11,0; – равносильные преобразования;
7500 = 0,75×104; 0,110×102 = 11; – неравносильные преобразования.
Здесь два нуля в первом и один ноль во втором выражениях переведены в разряд незначащих цифр, поэтому следует использовать записи 7500 = 0,7500×104 и 0,110×102 = 11,0.
5) При вычислениях желательно сохранять такое количество значащих цифр, чтобы их число не превышало числа верных цифр более чем на одну – две единицы.
6) Верные значащие цифры числа характеризуют ориентировочно относительную погрешность по схеме: одна верная цифра 10%, две – 1%, три – 0,1% и т.д. Верные значащие цифры после запятой характеризуют абсолютную погрешность или в «узком» или в «широком» смысле.
Нормализованная форма числа. Приближенные числа принято записывать таким образом, чтобы все цифры числа, кроме нулей впереди, если они есть, были значащими и верными цифрами.
Обычную форму записи числа, рассмотренную выше, называют записью с фиксированной точкой, а числа 0,63750×106; 637,50×103 и 6,3750×105 записаны в форме с плавающей точкой.
Запись числа с плавающей точкой, как следует из примера, не является однозначной. Для устранения этой неоднозначности принято первый множитель брать меньше единицы, и он должен состоять только из значащих цифр (кроме нуля целых), т.е. первая цифра после запятой всегда отлична от нуля.
Такая форма записи числа называется нормализованной. В данном примере ею является запись 0,63750×106, а для числа –0,00384 нормализованная форма –0,384×10–2.
Итак, запись числа х в нормализованной форме имеет вид
х = х 0×10 р; где 0,1 £ | х 0 | < 1.
Число х 0 называется мантиссой числа х, а число р – его порядком. Например, для числа 620 = 0,620×103 мантиссой является 0,620, а порядком – число 3. Заметим, что в этой записи все цифры после запятой верные.
7.Прямая и обратная задача теории погрешностей:
Прямая задача теории погрешностей
Пусть в некоторой области G n -мерного числового пространства рассматривается непрерывно дифференцируемая функция y = f (x 1,..., xn).
Пусть в точке (x 1,..., xn), принадлежащей области G, нужно вычислить ее (функции) значение. Известны лишь приближенные значения аргументов (а 1,..., аn) Î G, и их погрешности. Естественно, что это будет приближенное значение y * = f (а 1, а 2,..., аn).
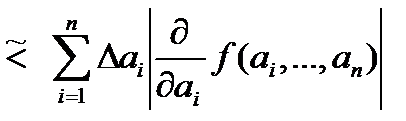 Нужно оценить его абсолютную погрешность:
Нужно оценить его абсолютную погрешность:
D y * = | y – y * |
 Для функции одного аргумента y = f (x) ее абсолютная погрешность, вызываемая достаточно малой погрешностью D а, оценивается величиной
Для функции одного аргумента y = f (x) ее абсолютная погрешность, вызываемая достаточно малой погрешностью D а, оценивается величиной
D y * =
Обратная задача теории погрешностей
Она состоит в определении допустимой погрешности аргументов по допустимой погрешности функции.
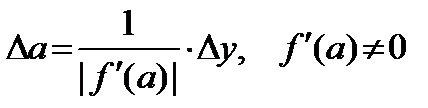 Для функции одной переменной y = f (x) абсолютную погрешность можно вычислить приближенно по формуле:
Для функции одной переменной y = f (x) абсолютную погрешность можно вычислить приближенно по формуле:
Для функций нескольких переменных y = f (x 1,..., xn) задача решается при следующих ограничениях.
Если значение одного из аргументов значительно труднее измерить или вычислить с той же точностью, что и значение остальных аргументов, то погрешность именно этого аргумента и согласовывают с требуемой погрешностью функции.
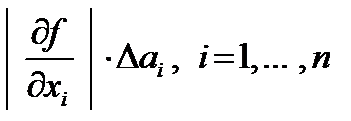 Если значения всех аргументов можно одинаково легко определить с любой точностью, то применяют принцип равных влияний, т.е. учитывают, что все слагаемые
Если значения всех аргументов можно одинаково легко определить с любой точностью, то применяют принцип равных влияний, т.е. учитывают, что все слагаемые
равны между собой. Тогда абсолютные погрешности всех аргументов определяются формулой:
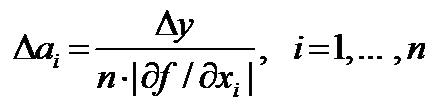
8.Устойчивость, корректность и сходимость численных методов:
Пусть в результате решения задачи по исходному значению величины х находится значение искомой величины у. Если исходная величина имеет абсолютную погрешность D х, то решение у имеет погрешность D у.
Задача называется устойчивой по исходному параметру х, если решение у непрерывно зависит от х, т.е. малое приращение исходной величины х приводит к малому приращению искомой величины у. Другими словами, малые погрешности в исходной величине приводят к малым погрешностям в результате расчетов.
Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или вовсе к неверному результату.
Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным.
Понятие сходимости численного решения вводится для итерационных процессов. По результатам многократного повторения итерационного процесса получаем последовательность приближенных значений. Говорят, что эта последовательность сходится к точному решению, если.
Таким образом, для получения решения задачи с необходимой точностью ее постановка должна быть корректной, а используемый численный метод должен обладать устойчивостью и сходимостью. Эти понятия будут рассматриваться в последующих разделах курса.
9.Основные требования к выбору численных методов:
Рассмотренные выше вопросы о погрешностях являются одними из важнейших моментов при выборе численного метода. В основе выбора численного метода лежат следующие соображения.
1) Можно утверждать, что нет ни одного метода, пригодного для решения всех задач одного и того же класса. Поэтому всегда стоит задача выбора численного метода (ЧМ), сообразуясь из конкретной технической задачи.
2) Численный метод можно считать удачно выбранным:
– если его погрешность в несколько раз меньше неустранимой погрешности, а погрешность округлений в несколько раз меньше погрешности метода;
– если неустранимая погрешность отсутствует, то погрешность метода должна быть несколько меньше заданной точности;
– завышенное снижение погрешности численного метода приводит не к повышению точности результатов, а к необоснованному увеличению объема вычислений.
3) Предпочтение отдается методу, который:
– реализуется с помощью меньшего числа действий;
– требует меньшего объема памяти ЭВМ;
– логически является более простым.
Перечисленные условия обычно противоречат друг другу, поэтому часто при выборе численного метода приходится соблюдать компромисс между ними.
4) Численный метод должен обладать устойчивостью и сходимостью.
5) По возможности нужно прибегать к существующему программному обеспечению ЭВМ для решения типовых задач.
6) Нужно помнить всегда, что ЭВМ многократно увеличивает некомпетентность Исполнителя технической задачи.
10.СЛАУ как математические модели вычислительной математики:
Системы линейных алгебраических уравнений (СЛАУ) являются важной математической моделью линейной алгебры. На их базе ставятся такие практические математические задачи, как:
– непосредственное решение линейных систем;
– вычисление определителей матриц;
– вычисление элементов обратных матриц;
– определение собственных значений и собственных векторов матриц.
Решение линейных систем является одной из самых распространенных задач вычислительной математики. К их решению сводятся многочисленные практические задачи нелинейного характера, решения дифференциальных уравнений и др.
Вторая и третья задачи являются также и компонентами технологии решения самих линейных систем.
 Обычно СЛАУ n -го порядка записывается в виде
Обычно СЛАУ n -го порядка записывается в виде
или в развернутой форме

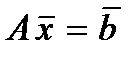
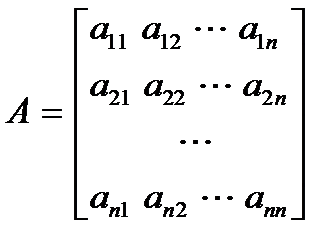 или в векторной форме (2)
или в векторной форме (2)
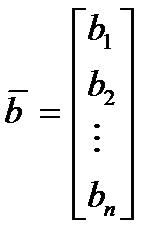
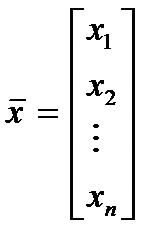 где
где
В соотношениях (2):
А называется основной матрицей системы с n 2 элементами;
= (x 1, x 2,..., xn)Т – вектор-столбец неизвестных;
= (b 1, b 2,..., bn)Т – вектор-столбец свободных членов.
Определителем (детерминантом – det) матрицы А n -го порядка называется число D (det A), равное

Здесь индексы a, b,..., w пробегают все возможные n! перестановок номеров 1, 2,..., n; k – число инверсий в данной перестановке.
Первоначальным при решении СЛАУ (1) является анализ вида исходной матрицы А и вектора-столбца свободных членов в (2).
Если все свободные члены равны нулю, т.е. = 0, то система называется однородной. Если же ¹ 0, или хотя бы одно bi ¹ 0 (), то система (2) называется неоднородной.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель | A | ¹ 0. При этом система (1) имеет единственное решение.
При | A | = 0 матрица А называется вырожденной, или особенной, а система (1) не имеет решения, либо имеет бесконечное множество решений.
Если | A |» 0 система (1) называется плохо обусловленной, т.е. решение очень чувствительно к изменению коэффициентов системы.
В ряде случаев получаются системы уравнений с матрицами специальных видов: диагональные, трехдиагональные (частный случай ленточных), симметричные (аij = aji), единичные (частный случай диагональной), треугольные и др.
Решение системы (2) заключается в отыскании вектора-столбца = (x 1, x 2,..., xn)Т, который обращает каждое уравнение системы в тождество.
Существуют две величины, характеризующие степень отклонения полученного решения от точного, которые появляются в связи с округлением и ограниченностью разрядной сетки ЭВМ, – погрешность e и «невязка» r:
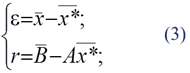
где 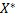 – вектор решения. Как правило, значения вектора
– вектор решения. Как правило, значения вектора 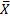 – неизвестны.
– неизвестны.
Доказано, что если e» 0, то и r = 0. Обратное утверждение не всегда верно. Однако если система не плохо обусловлена, для оценки точности решения используют невязку r.
11.Методы решения СЛАУ:
Методы решения СЛАУ делятся на две группы:
– прямые (точные) методы;
– итерационные (приближенные) методы.
К прямым методам относятся такие методы, которые, в предположении, что вычисления ведутся без округлений, позволяют получить точные значения неизвестных. Они просты, универсальны и используются для широкого класса систем. Однако они не применимы к системам больших порядков (n < 200) и к плохо обусловленным системам из-за возникновения больших погрешностей. К ним можно отнести: правило Крамера, методы обратных матриц, Гаусса, прогонки, квадратного корня и др.
К приближенным относятся методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы лишь с заданной точностью. Это итерационные методы, т.е. методы последовательных приближений. К ним относятся методы простой итерации, Зейделя.
12.Правило Крамера:
Рассмотрим систему (1). Как отмечалось выше, если определитель этой системы не равен нулю, то будет иметь место единственное решение. Это необходимое и достаточное условие. Тогда по правилу Крамера
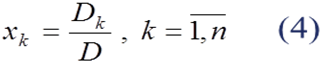
где Dk – определитель, получающийся из D при замене элементов a 1 k, a 2 k,..., ank k -го столбца (соответствующими) свободными членами b 1, b 2,..., bn из (1), или
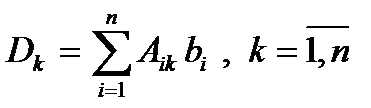
где Аik алгебраическое дополнение элемента aik в определителе D. Стоит существенная проблема вычисления определителей высоких порядков.
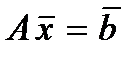 13.Метод обратных матриц:
13.Метод обратных матриц:
Дана система. Умножим левую и правую части этого выражения на А –1:


При его реализации стоит проблема нахождения обратной матрицы А –1, с выбором экономичной схемы ее получения и с достижением приемлемой точности. Эти вопросы рассмотрим ниже.
14.Метод Гаусса:
Этот метод является наиболее распространенным методом решения СЛАУ. В его основе лежит идея последовательного исключения неизвестных, в основном, приводящая исходную систему к треугольному виду, в котором все коэффициенты ниже главной диагонали равны нулю. Существуют различные вычислительные схемы, реализующие этот метод. Наибольшее распространение имеют схемы с выбором главного элемента либо по строке, либо по столбцу, либо по всей матрице. С точки зрения простоты реализации, хотя и с потерей точности, перед этими схемами целесообразней применять так называемую схему единственного деления. Рассмотрим ее суть.
Посредством первого уравнения системы (1) исключается х 1 из последующих уравнений. Далее посредством второго уравнения исключается х 2 из последующих уравнений и т.д. Этот процесс называется прямым ходом Гаусса. Исключение неизвестных повторяется до тех пор, пока в левой части последнего n -го уравнения не останется одно неизвестное хn
a ¢ nnxn = b ¢, (5)
где a ¢ nn и b ¢ – коэффициенты, полученные в результате линейных (эквивалентных) преобразований.
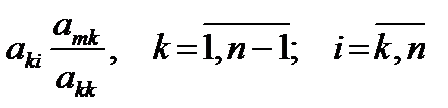 Прямой ход реализуется по формулам:
Прямой ход реализуется по формулам:
а * mi = ami – (6) 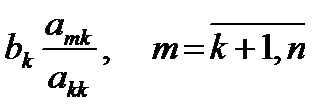
b * m = bm –
где
m – номер уравнения, из которого исключается xk;
k – номер неизвестного, которое исключается из оставшихся (n – k) уравнений, а также обозначает номер уравнения, с помощью которого исключается xk;
i – номер столбца исходной матрицы;
akk – главный (ведущий) элемент матрицы.
Во время счета необходимо следить, чтобы akk ¹ 0. В противном случае прибегают к перестановке строк матрицы.
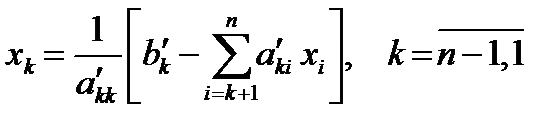 Обратный ход метода Гаусса состоит в последовательном вычислении xn, xn –1,..., x 1, начиная с (5) по алгоритму
Обратный ход метода Гаусса состоит в последовательном вычислении xn, xn –1,..., x 1, начиная с (5) по алгоритму
xn = b ¢ / a ¢ nn;
Точность полученного решения оценивается посредством «невязки» (3). В векторе невязки (r 1, r 2,..., rn)Т отыскивается максимальный элемент и сравнивается с заданной точностью e. Приемлемое решение будет, если r max < e. В противном случае следует применить схему уточнения решения.
Дата публикования: 2014-10-20; Прочитано: 2814 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
