Нормальное распределение

Одним из наиболее часто встречающихся распределений является нормальное распределение (его еще называют распределением Лапласа-Гаусса, или просто распределением Гаусса или Лапласа.). Оно играет огромную роль в теории вероятностей и ее приложениях.

Плотность функции нормального распределения имеет вид

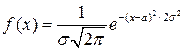. (2.8)

Функция нормального распределения имеет вид

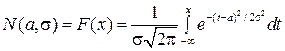. (2.9)

Однако часто вместо функции нормального распределения используется функция Лапласа F(x), и тогда

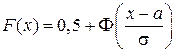, (2.10)

где 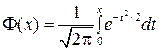– функция Лапласа.

Вероятность того, что случайная величина X, описываемая нормальным распределением, примет значение, принадлежащее интервалу (a,b), имеет вид

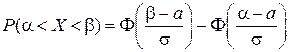. (2.11)

Вероятность того, что отклонение случайной величины X от математического ожидания по абсолютной величине меньше заданного положительного числа d, вычисляется по формуле:

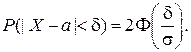(2.12)

В частности, если d=3s, то

P (| X – a |<3s) = 2F(3) = 0,9973.

Это равенство показывает, что во многих практических вопросах при рассмотрении нормального распределения можно пренебречь возможностью отклонения случайной величины от a больше, чем 3s. Это есть т.н. правило «трех сигм».

Пример 2.4. Рост мужчин определенной возрастной категории описывается нормальным законом распределения с математическим ожиданием a =165 см и средним квадратичным отклонением s=5 см. Какую долю костюмов 3-го роста (170-176 см) следует предусмотреть в общем объеме производства для данной возрастной категории?

Решение. Пусть X – рост в сантиметрах представителя данной возрастной категории. Тогда по формуле (2.11), где a=170 см и b=176 см, находим

.

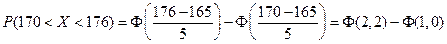Далее, по таблицам для функции Лапласа, находим

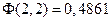и .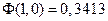

В результате получаем

,

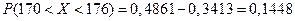т.е. доля костюмов 3-го роста должна составлять приблизительно 14,5% общего объема производства для данной категории мужчин.

Пример 2.5. Предположим, что в течение года цены на акции некоторой компании подчинялись нормальному закону распределения с математическим ожиданием, равным 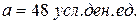, и стандартным отклонением, равным 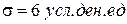. Чему равна вероятность того, что в случайно выбранный день обсуждаемого периода цена на акцию: а) отклонится от математического ожидания не более, чем на 10 усл. ден. ед.; б) будет более 60 усл. ден. ед.

Решение. Для ответа на первый вопрос воспользуемся формулой (2.12). Поскольку по условию задачи d=10, то находим

.

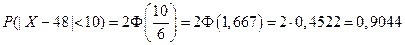Таким образом, в 90,4% случаях в течение обсуждаемого периода цена акции отклонялась от 48 усл. ден. ед. не более чем на 10 усл. ден. ед.

Для ответа на второй вопрос воспользуемся формулой (2.11):

,

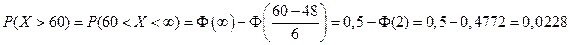т.е. только 2,3% случаях в течение рассматриваемого периода цена акции превышала 60 усл. ден. ед.