Горение пороха 1 страница

Для того чтобы началось горение порохового зер.на, ему необ­ходимо в некоторой точке поверхности сообщить тепловой им­пульс, способный вызвать взрывчатое превращение пороха. Этот процесс называется зажжением. Зажжение бездымного пороха происходит при температуре около 200° С, а зажжение дымного пороха — при температуре около 270° С.

После зажжения происходит воспламенение, т. е. процесс рас­пространения реакции взрывчатого превращения по поверхности порохового зерна. Скорость воспламенения зависит от сорта по­роха и внешних условий, главным образом от наружного дав­ления. С увеличением давления скорость воспламенения возра­стает.

При атмосферном давлении скорость воспламенения бездым­ного пороха равна 1 мм/с, а дымного пороха достигает 3000 мм/с.

В орудии зажжение и воспламенение порохового заряда при выстреле производятся с помощью воспламенителя, состоящего обычно из дымного пороха, создающего при сгорании давление пороховых газов примерно 50-10⁵Н/м².

Горением пороха называется процесс распространения реак­ции взрывчатого превращения от поверхности в глубь порохового зерна.

Механизм горения пороха состоит в термическом разложении (газификации) нитроклетчатки в поверхностном слое 1 (рис. 1.4) и в химическом взаимодействии газообразных продуктов разло­жения в зоне 2 с образованием пламени и выделением большого количества тепла.

На рис. 1.4 показан график изменения темпе­ратуры в толщине пороха и в пороховых газах у поверхности зер­на от начальной температуры поро­ха То до температуры горения Т\. На­грев поверхностного слоя на глуби­ну х_г происходит за счет теплопередачи от раскаленных пороховых газов зо­ны 2, причем в поверхностном слое зерна толщиной х_р устанавливается температура Т_п, при которой идет про­цесс разложения нитроклетчатки. При сжигании пороха в открытом про­странстве получены следующие дан­ные: для пироксилинового пороха Т_п= = 525±48°К, для нитроглицеринового пороха Г_Д = 603±45°К; величина х_р составляет около 5% толщины прогре­того слоя х_г.

Горение пороха характеризуется величиной скорости горения.

Скоростью горения пороха «' называется скорость распростране­ния реакции взрывчатого превращения пороха по нормали к по­верхности порохового зерна:

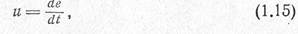
где е — толщина слоя сгоревшего пороха, т. е. расстояние от по­верхности порохового зерна, на которое распространяется реакция взрывчатого превращения за время (.

Скорость горения пороха зависит от сорта пороха, наруж­ного давления, начальной температуры пороха, скорости обдува поверхности порохового зерна.

Зависимость скорости горения от давления р называется законом скорости горения и в общем случае выражается эмпири­ческой формулой

где а, Ь, V — эмпирические коэффициенты.

В артиллерийских орудиях при больших давлениях справед­лив линейный закон

Эмпирический коэффициент скорости горения и_и как следует из формулы (1.17), представляет собой скорость горения в м/с

при давлении, равном 1 Н/м², и имеет размерность Ве­

личина «_ь очевидно, должна зависеть от сорта, начальной тем­пературы и скорости обдува пороха.

В табл. 1.4 приведены увеличенные в 10^п раз значения u для различных сортов пороха при температуре пороха l₃=15°С и при отсутствии обдува пороха.

Величина и_х возрастает примерно на 28% при увеличении со­держания азота в порохе на 1% и уменьшается примерно на 13% с увеличением содержания влаги в порохе на 1%.

Для всех существующих бездымных порохов можно принять следующую опытную зависимость:

из которой следует, что с увеличением калорийности скорость го­рения пороха возрастает линейно.

Зависимость скорости горения пороха от его начальной темпе­ратуры l₃ имеет следующий вид:

где Б — эмпирический коэффициент, равный в среднем 320.

Для существующих бездымных порохов при увеличении на­чальной температуры на ГС скорость горения увеличивается примерно на 0,16%.

Зависимостью скорости горения пороха от скорости обдува при горении пороха в артиллерийском орудии, когда пороховые зерна перемещаются вместе с пороховыми газами, можно прене­бречь.

В основу изучения горения порохового заряда, состоящего из большого числа пороховых зерен, положены три основных поло­жения, полученных из многолетней артиллерийской практики:

— все пороховые зерна заряда имеют одинаковую форму и размеры;

— воспламенение всех пороховых зерен заряда происходит мгновенно;

горение всех пороховых зерен заряда происходит во всех точках поверхности с одинаковой скоростью, т. е. параллельными слоями

Эти положения составляют сущность так называемого геомет- ческого "закона горения пороха. В некоторых случаях (недостаточные воспламенителя, очень узкие каналы в пороховых зернах) геометрический закон горения может существенно отличаться от действительного, называемого физическим законом горения по­роха.

§ 1.4. ОБРАЗОВАНИЕ ПОРОХОВЫХ ГАЗОВ

В результате горения пороха идет процесс образования поро­ховых газов.

Законом образования пороховых газов называется зависимость между относительной массой сгоревшего пороха и относительной толщиной слоя сгоревшего по­роха z:

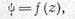
где

— масса сгоревшего пороха;

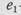— половина толщины горя­щего слоя порохового зерна.

Величины при горении

пороха изменяются от нуля в мо­мент начала горения

до единицы в момент окон­чания горения.

Аналитическое выражение для закона образования пороховых газов при геометрическом законе горения пороха можно получить теоретическим путем.

Обозначим через п число зерен в заряде, через начальный объем порохового зерна, а через объем порохового зерна в про­извольныймомент времени. Тогда начальная масса заряда будет равна масса сгоревшего пороха и выраже­

ние для примет вид

Таким образом, оказалось, что для определения ф необходимо рассмотреть изменение объема одного порохового зерна. Рассмотрим горение порохового зерна ленточной формы

Пусть в произвольный момент времени пороховая лента обго­рит со всех сторон на толщину слоя е. Первоначальный объем ленты

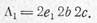
Объем ленты в рассматриваемый момент времени

Используя формулу (1.21) и сделав преобразования, получим выражение

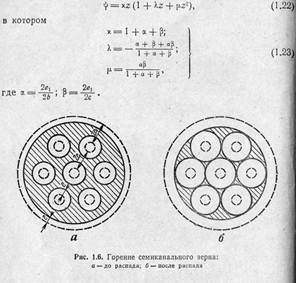
Выражение (1-22) является общим выражением для закона! образования пороховых газов, справедливым для пороховых зенрен распространенной формы. Величины х, ~к, р называются коэффициентами формы порохового зерна и будут принимать различ­ные значения для пороховых зерен различной формы.

Распространенные в артиллерии зерненые пороха с семью каналами горят с распадом зерна, который происходит в момент соприкосновения поверхностей каналов друг с другом (рис. 1.6). При этом образуется 6 внешних и 6 внутренних звездок, которые! составляют соответственно 12 и 3% всего объема зерна.

Таким образом, горение семиканального порохового зерна про­исходит в две фазы: в первой фазе сохраняется форма семиканального зерна, во второй фазе идет горение звездок. Очевидно коэффициенты формы в каждой фазе будут свои.

В табл. 1.5 приведены размеры и коэффициенты формы для ряда пороховых зерен.

На практике обычно ввиду относительной малости р поль­зуются двучленным выражением закона образования пороховых

газов

Тогда форма порохового зерна будет определяться только одним коэффициентом г., так как второй коэффициент X однозначно опре­деляется через х:

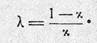
Относительное количество газов, образовавшихся при горении пороха в единицу времени, т. е. относительный секундный приход газов, называется быстротой газообразования. Дифференцируя выражение (1.21)

по времени, получим

Введем в формулу (1.25) поверхность S горения порохового зерна, тогда

И

Поверхность зерна до начала горения обозначим через Si. Деля раж ^Н°^{ЖаЯ прав}У^{ю часть} равенства (1.26) на S, и учитывая вы- ' ения (1.15) и (1.17) для скорости горения, будем иметь

Рассмотрим влияние на быстроту газообразования величины

. При неизменном давлении секундный приход газов увеличи­вается с увеличением величины 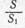и уменьшается с ее уменьше­нием. В случае постоянства величины секундный приход газов при постоянном давлении будет оставаться постоянным.

Величину обозначают через о и называют коэффициентом прогрессивности пороха:

Порох, у которого при горении поверхность увеличивается и следовательно, а>1, называется порохом прогрессивной формы.

Порох, у которого при горении поверхность уменьшается и, сле­довательно, а<1, называется порохом дегрессивной формы.

Порох, у которого при горении поверхность не изменяется и следовательно, а=1, называется порохом нейтральной формы.

Коэффициент прогрессивности а при горении пороха не остается постоянным, а является функцией г:

Найдем производную от о по z:

Знак производной определяет характер изменения коэффициента прогрессивности а.

Ввиду относительной малости л знак производной 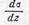и, сле­довательно, степень прогрессивности формы пороха будут зависеть от знака X.

Из табл. 1.5 видим, что пороховые зерна в форме куба, шара, ленты, трубки, звездок после распада семиканального зерна имеют Х<0, т. е. являются дегрессивными; семиканальные зерна в первой фазе горения и трубка, бронированная с торцов и наружной по­верхности, имеют Х>0, т. е. обладают прогрессивной формой. Строго нейтральной будет форма трубки с бронированными тор­цами, для которой Х = 0. Пороховое зерно в виде трубки прибли­жается к зерну нейтральной формы.

На рис. 1.7 и 1.8 изображены соответственно кривые ф = /(г) и о = /(г) для тех форм пороховых зерен, которые рассмотрены в табл. 1.5; при этом табличные порядковые номера сохранены и на рисунках. Величины as и ф₃ отвечают моменту распада семика­нального зерна. Рисунки показывают, что при сгорании пороха на одну и ту же толщину слоя, например при г = 0,5, поверхность горения (а) будет тем меньше, а относительное количество выде­лившихся газов (ф) тем больше, чем дегрессивнее форма пороха.

Это обстоятельство имеет большое значение для артиллерийской практики. При заданном наибольшем давлении пороховых газов в орудии увеличение прогрессивности формы пороха позволяет увеличить массу порохового заряда и, следовательно, начальную скорость снаряда.

Рис. 1.7. Закон образования газов Рис. 1.8. Коэффициент про­ грессивности § 1.5. ДАВЛЕНИЕ ПОРОХОВЫХ ГАЗОВ В ПОСТОЯННОМ ОБЪЕМЕ

При горении пороха в постоянном объеме, например в мано­метрической бомбе, вследствие непрерывного поступления порохо­вых газов давление р будет непрерывно возрастать до величины наибольшего давления Р в момент окончания горения.

Величина давления в любой момент времени определяется с помощью уравнения состояния газа с учетом коволюма (1.12):

откуда

где да— удельный объем газов.

При отсутствии теплообмена в постоянном объеме пороховые горен ^иметь постоянную температуру Т — Т во все время

К росматриваемому моменту времени сгорит и превратится в пороховые газы пороха, а останется ш(1— ф) пороха. Образовавшиеся пороховые газы будут занимать объем, равный объему

каморы Wo, за вычетом объема, занимаемого несгоревшим порой

хом: где 8— плотность пороха.

Соответствующий удельный объем пороховых газов w будет равен отношению объема, занимаемого пороховыми газами, к их массе:

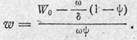
Подставляя это выражение в формулу (1.32) и учитывая, что 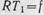, найдем

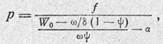
или |

Знаменатель выражения (1.33) представляет собой свободный объем каморы W^, т. е. объем каморы за вычетом объема, зани­маемого несгоревшим порохом и самими молекулами пороховых газов:

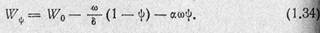
Введем приведенную длину свободного объема каморы

которая будет использоваться дальше.

Вводя плотность заряжания А, можем записать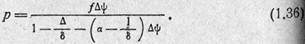

Ввиду того что величины а и 1/8 мало отличаются друг от друга, влияние последнего слагаемого в знаменателе незначительно, а зависимость давления пороховых газов от относительной массь сгоревшего пороха близка к линейной.

Наибольшее давление пороховых газов р—Р достигается при ф=1 и называется полным пиростатическим давлением. Формулу для Р получим из выражения (1.33) или выражения (1.36):

или

формула впервые была получена Л. Н. Шишковым для дымного

пороха в 1857 г.

Уравнение (1.38) представляет собой уравнение гиперболы относительно Д. С увеличением плотности заряжания А наиболь­шее давление пороховых газов в постоянном объеме Р будет расти

и при приближении А к величине, равной 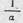, будет стремиться к бесконечности, так как знаменатель в выражении (1.38) будет стремиться к нулю.

Зависимость давления пороховых газов в постоянном объеме от времени имеет вид

где —давление в момент начала горения порохового заряда, равное атмосферному давлению или давлению пороховых газов воспламенителя; % — пиростатический параметр условий заряжания:

Из выражения (1.39) следует, что параметр т численно равен времени горения порохового заряда, при котором давление поро­ховых газов в постоянном объеме увеличится в е = 2,72 раза.

Полученные в пиростатике выражения для давления пороховых газов применяются при вычислении величины давления или вели­чины сгоревшей, части порохового заряда в орудии в предвари­тельном периоде.

Как видим, при сгорании всего заряда в каморе орудия до начала движения снаряда (при мгновенном сгорании заряда) давление пороховых газов может достигнуть нескольких десятков тысяч атмосфер, что значительно превышает допустимое по условиям прочности ствола давление.

§ 2.1. РАСШИРЕНИЕ ПОРОХОВЫХ ГАЗОВ

При движении снаряда по каналу ствола орудия происходят расширение пороховых газов и переход тепловой энергии газов в механическую работу, основная и полезная часть которой равна кинетической энергии снаряда; при этом температура пороховых газов будет понижаться.

В кинетическую энергию снаряда переходит 25—40% всей тепловой энергии, выделяющейся при сгорании порохового заряда. Приблизительно половина всей тепловой энергии пороховых газов при выстреле выбрасывается в атмосферу в виде тепловой энергии струи газов и рассеивается. Некоторая часть тепловой энергии (1—10%) переходит в

кинетическую энергию пороховых газов и также в значительной степени теряется при истечении пороховых газов из канала ствола. При этом в атмосфере возникают разнообразные явления, связанные с преобразованием энергии: перемешивание и нагрев воздуха, возникновение ударных волн (дульной волны), свечение струи газов (дульное пламя), электризация облака пороховых газов, химические реакциии т. п. Большинство перечисленных явлений играет отрицательную роль.

Кинетическая и тепловая энергия пороховых газов в орудиях с дульным тормозом частично (до 1 % всей тепловой энергии) полезно расходуется на работу дульного тормоза для уменьшения силы отдачи. На откат ствола, т. е. в кинетическую энергии откатных частей орудия, переходит 0,5—1% всей тепловой энергии. Тепловая энергия пороховых газов и кинетическая энергий откатных частей орудия в незначительных количествах используются для совершения полезных работ, например для заряжаних орудия в автоматах, наката ствола, продувки канала ствола (эжектирование) и т. д. Некоторая часть тепловой энергии пороховых газов (до 5%) посредством теплопередачи переходит стенки ствола, а затем в охлаждающую ствол жидкость или в атмосферу.

Считая, что расширение пороховых газов орудия происходя без теплообмена, т. е. адиабатически, на основании первого закон

термодинамики можно получить основное уравнение пиродинамики, описывающее процесс расширения пороховых газов в ору­дии. Для адиабатического процесса сумма работ

, совершен­ных пороховыми газами массой при расширении, равна изме­нению их внутренней тепловой энергии:

_гд_е — тепловая энергия 1 кг пороховых газов в момент их образования;

— тепловая энергия 1 кг пороховых газов в рассматривае­мый момент времени.

Из термодинамики известно, что

где C_w — удельная теплоемкость пороховых газов при постоян­ном объеме;

— температура пороховых газов в градусах абсолютной шкалы.

Для момента образования пороховых газов будем иметь 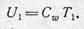Тогда уравнение (2.1) получит вид

Воспользуемся еще одним соотношением термодинамики:

где R — удельная газовая постоянная;

С_р — удельная теплоемкость пороховых газов при постоянном

давлении.

Введем параметр расширения пороховых газов 0, определяе­мый равенством

в котором k представляет собой показатель адиабаты: Можем записать

после чего выражение (2.4) для примет вид

Это и есть основное уравнение пиродинамики.

Под величиной р здесь понимается некоторое постоянное во всех точках заснарядного пространства среднее давление пороховых газов, называемое баллистическим давлением.

Основное уравнение пиродинамики выражает собой закон сохранения энергии при выстреле. Оно записывается для произвольного момента времени, когда сгорит ф-я часть порохового заряда, а снаряд пройдет путь I и будет иметь скорость v. В правой части уравнения (2.10) стоит разность внутренней (тепловой) энергий образовавшихся пороховых газов до их расширения и после расширения (выражена в единицах работы). В левой части стоил механическая работа, которую совершат пороховые газы к рассматриваемому моменту времени.

Сила пороха f определяет работоспособность 1 кг пороха, а|произведение fшф —работоспособность сгоревшей части заряда при изобарном процессе расширения пороховых газов. При этом

часть тепла, выделяемого сгоревшим порохом, будет тратиться на под держание постоянного давления. При адиабатическом процессе расширения пороховых газов, который происходит в орудии, все тепло идет на совершение работы. Поэтому для получения вели­чины тепловой энергии произведение делится на параметр рас­ширения который, следовательно, численно равен отношению работы расширения газов изобарного и адиа­батического процессов. Величина для поро­ховых газов в среднем равна 0,2, т. е. работа пороховых газов при изобарном процессе со­ставляет 20% работы при адиабатическом процессе.

§ 2.2. ДВИЖЕНИЕ СНАРЯДА В КАНАЛЕ СТВОЛА

Рис. 2.1. Нарезка по­стоянной крутизны

В нарезном стволе артиллерийского ору­дия снаряд совершает поступательное и вра­щательное движения. Движущей силой, при­водящей в движение снаряд, является сила давления пороховых газов, равная проекции на ось канала ствола элементарных сил дав­ления пороховых газов, действующих на за- поясковую часть снаряда. Давление порохо­вых газов у дна снаряда р_сн будет меньше среднего баллистического давления р и, тем более, давления у дна канала ствола так как процесс расширения пороховых газов (волна расши­рения), происходящий вследствие поступательного движения сна­ряда, всегда начинается у дна снаряда и затем распространяется к дну каморы. При этом в результате перепада давлений по­роховые газы и несгоревший порох получают также посту­пательное движение. Величина движущей силы определяется так:

Кроме движущей силы на снаряд будут действовать силы реакции ствола, возникающие на поверхностях контакта снаряда со стен­ками ствола.

Нарезной ствол на участке длиной имеет нарезку постоянной

или прогрессивной крутизны. Если ствол разрезать по образующей и развернуть на плоскость, то при постоянной крутизне направления нареза совпадает с направлением прямой линии, идущей Углом к образующей канала ствола (рис. 2.1). Угол а называется углом наклона нарезов. Расстояние по оси канала ствола, на котором нарез делает полный оборот, называется длиной хода нареза. Относительная длина хода нареза обозначается через

Движение снаряда по каналу ствола начинается при некото­ром давлении пороховых газов р_н, достаточном для начала вре­зания ведущих поясков в нарезы или для начала освобождения

снаряда из дульца гильзы. Участок между положениями дна снаряда в момент начала движения и в момент полного врезания ведущих поясков в нарезы называется участком форсирования.

На участке форсирования происходит врезание ведущих пояс ков снаряда в нарезы. При этом со стороны ствола на ведущий поясок снаряда будет действовать сила реакции, проекция которой на ось канала ствола называется силой сопротивления врезанию F_Вр. Обычно рассматривают величину сопротивления врезанию П|

которую определяют экспериментально путем продавливания сна ряда через канал ствола.

На рис. 2.2 приведена упрощенная зависимость сопротивления врезанию от пути снаряда. В случае раздельного заряжания орудия снаряд начинает врезаться в нарезы при П = П_Н, затем нч протяжении пути l_в, соответствующем ширине ведущего пояска сопротивление врезанию линейно возрастает до П = П_тах и далее остается постоянным до конца участка форсирования /ф. При дальнейшем движении снаряда сопротивление движению будет незначительным. Таким образом, началу движения снаряда отвечает условие