 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Частинні похідні n-го порядку
|
|
Частинні похідні 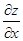 і
і  функції z=f(х;y) є деякими функціями змінних х та y і, в свою чергу, можуть мати частинні похідні і по х, і по y, які називаються частинними похідними другого порядку від функції z=f(х;y). Позначаються і визначаються похідні другого порядку так:
функції z=f(х;y) є деякими функціями змінних х та y і, в свою чергу, можуть мати частинні похідні і по х, і по y, які називаються частинними похідними другого порядку від функції z=f(х;y). Позначаються і визначаються похідні другого порядку так:
 (9.31)
(9.31)
 (9.32)
(9.32)
 (9.33)
(9.33)
 (9.34)
(9.34)
Теорема 1. Якщо функція z=f(х;y) та її частинні похідні 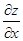 ,
,  ,
,  ,
,  неперервні у точці М(х;y) і в деякому околі цієї точки, то у цій точці
неперервні у точці М(х;y) і в деякому околі цієї точки, то у цій точці
 =
=  . (9.35)
. (9.35)
Частинні похідні другого порядку знову можна диференціювати по х та по y. При цьому отримаємо частинні похідні третього порядку, яких для функції двох змінних z=f(х;y) буде вісім:
 (9.36)
(9.36)
 (9.37)
(9.37)
 (9.38)
(9.38)
 (9.39)
(9.39)
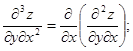 (9.40)
(9.40)
 (9.41)
(9.41)
 (9.42)
(9.42)
 (9.43)
(9.43)
Означення 20. Частинною похідною n-го порядку функції z=f(х;y) називається частинна похідна першого порядку від частинної похідної (n-1)-го порядку.
Приклад 14. Для функції  довести, що
довести, що  .
.
Знайдемо спочатку частинні похідні першого та другого порядків заданої функції:


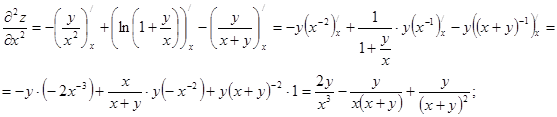



Тепер розглянемо вираз та підставимо знайдені похідні:

що і треба було довести.
Приклад 15. Знайти частинні похідні другого порядку функції 
Знайдемо частинні похідні першого порядку:



А тепер знайдемо частинні похідні другого порядку:




Таким чином


 .
.
10. ЕКСТРЕМУМ ФУНКЦІЇ z=f(х;y)
Означення 21. Точка M0(x0;y0) називається точкою локального максимуму функції z=f(х;y) якщо існує такий окіл точки M0, в якому для будь-якої точки M(x;y) (окрім самої точки M0(x0;y0)) виконується нерівність
 . (10.44)
. (10.44)
Означення 22. Точка M0(x0;y0) називається точкою локального мінімуму функції z=f(х;y), якщо існує такий окіл точки M0, в якому для будь-якої точки M(x;y) (окрім самої точки M0(x0;y0)) виконується нерівність
 . (10.45)
. (10.45)
Означення 23. Локальні мінімуми і максимуми функції називаються її локальними екстремумами. Точка, в якій досягається локальний екстремум функції, називається точкою локального екстремуму.
Приклад 16. Функція 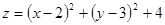 досягає у точці M0(2;3) локального мінімуму. Дійсно,
досягає у точці M0(2;3) локального мінімуму. Дійсно,  , крім того для всіх
, крім того для всіх  і
і 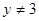 маємо
маємо  і
і  , а
, а 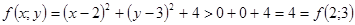 , тобто
, тобто  для всіх
для всіх  і
і 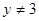 . Отже,
. Отже,  .
.
Теорема 2 (необхідні умови локального екстремуму).
Якщо диференційована функція z=f(х;y), має в точці M0(x0;y0) локальний екстремум, то виконуються рівності:
 . (10.46)
. (10.46)
Означення 24. Точки, в яких виконуються рівності (6.34), або в яких 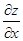 і
і  не існують, називаються критичними або стаціонарними точками для функції z=f(х;y).
не існують, називаються критичними або стаціонарними точками для функції z=f(х;y).
Теорема 3 (достатні умови локального екстремуму).
Нехай у точці M0(x0;y0) і деякому її околі функція z=f(х;y) має неперервні частинні похідні до третього порядку включно; нехай, крім того,  . Позначимо
. Позначимо  і
і  . Тоді:
. Тоді:
функція z=f(х;y) досягає в точці M0(x0;y0) локального максимуму, якщо  ;
;
функція z=f(х;y) досягає в точці M0(x0;y0) локального мінімуму, якщо  ;
;
функція z=f(х;y) не має в точці M0(x0;y0) локального екстремуму, якщо  ;
;
функція z=f(х;y) може мати і може не мати в точці M0(x0;y0) локального екстремуму, якщо ∆=0 (в цьому випадку потрібно провести додаткові дослідження).
Приклад 17. Дослідити на екстремум функцію 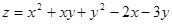 .
.
Спочатку знайдемо критичні точки, для чого використаємо необхідні умови (6.34) локального екстремуму.
Так як  , то маємо систему рівнянь
, то маємо систему рівнянь
 розв’язком якої є
розв’язком якої є  .
.
Отже, точка  – критична точка.
– критична точка.
Тепер перевіримо для цієї точки достатні умови локального екстремуму.
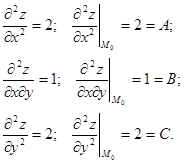
Маємо  і
і 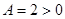 , а отже, в точці
, а отже, в точці  задана функція має локальний мінімум і
задана функція має локальний мінімум і  .
.
Приклад 18. Дослідити на екстремум функцію 
Знайдемо критичні точки, використовуючи необхідні умови локального екстремуму.
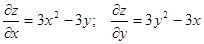 .
.

і, отже, маємо 2 критичні точки М1(0;0) і М2(1;1).
Знайдемо частинні похідні другого порядку  .
.
умов локального екстремуму.

 і згідно з теоремою 3 у точці М1(0;0) задана функція локального екстремуму не має.
і згідно з теоремою 3 у точці М1(0;0) задана функція локального екстремуму не має.
Тепер розглянемо, чи виконуються достатні умови локального екстремуму у точці М2(1;1).

 .
.
Згідно з теоремою 3 у точці М2(1;1) задана функція досягає локального мінімуму і  .
.
Приклад 19. Дослідити на екстремум функцію  .
.
Згідно з теоремою 2 необхідні умови існування локального екстремуму виглядять так:
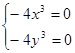 .
.
Розв’язком цієї системи рівнянь є 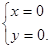
Отже, критична точка М0(0;0).
Знайдемо другі частинні похідні:

Тоді  .
.
Згідно з теоремою 3 потрібні додаткові дослідження. Проведемо їх:
 а для всіх
а для всіх 
 ; отже
; отже
 , тобто
, тобто  для всіх
для всіх  . Згідно з означенням 20 у точці М0(0;0) задана функція досягає локального максимуму і
. Згідно з означенням 20 у точці М0(0;0) задана функція досягає локального максимуму і  .
.
Дата публикования: 2014-11-18; Прочитано: 6125 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
