|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вектор-функция скалярного аргумента
|
|
Основные понятия
1. Пусть дан радиус-вектор 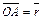 , концом которого является точка A (x; y; z). Выражая этот вектор через проекции на оси координат, получим
, концом которого является точка A (x; y; z). Выражая этот вектор через проекции на оси координат, получим
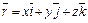 . (1)
. (1)
Пусть проекции вектора 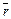 есть функции некоторого параметра t:
есть функции некоторого параметра t:
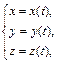 (2)
(2)
тогда формула (1) примет вид
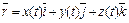 или коротко
или коротко 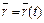 . (3)
. (3)
При изменении t изменяются x, y, z – координаты точки А и, следовательно, изменяется вектор 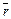 по величине и по направлению, поэтому вектор
по величине и по направлению, поэтому вектор 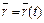 называют вектор-функцией скалярного аргумента t.
называют вектор-функцией скалярного аргумента t.
Линию в пространстве, которую описывает точка А – конец вектора 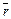 называют годографом этого вектора. Уравнения (2) называются параметрическими уравнениями линии в пространстве, а уравнение (3) – векторным уравнением линии в пространстве.
называют годографом этого вектора. Уравнения (2) называются параметрическими уравнениями линии в пространстве, а уравнение (3) – векторным уравнением линии в пространстве.
2. Пусть 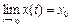 ,
, 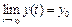 ,
, 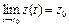 , тогда говорят, что вектор
, тогда говорят, что вектор 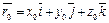 есть предел вектора
есть предел вектора 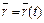 , и пишут
, и пишут
 . (4)
. (4)
3. Производной вектор-функции 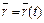 по скалярному аргументу t называют предел отношения приращения вектор-функции
по скалярному аргументу t называют предел отношения приращения вектор-функции 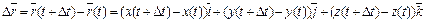 к приращению D t скалярного аргумента t, т. е.
к приращению D t скалярного аргумента t, т. е.
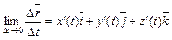 (5)
(5)
и обозначают символом 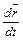 или
или 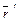 .
.
Таким образом, по определению
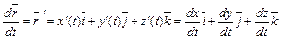 . (6)
. (6)
4. Производная вектор-функции 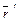 является новой вектор-функцией и называется производной первого порядка. Производная от производной
является новой вектор-функцией и называется производной первого порядка. Производная от производной 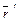 называется производной второго порядка и обозначается
называется производной второго порядка и обозначается 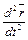 или
или 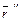 , т. е.
, т. е.
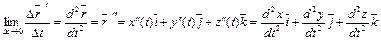 . (7)
. (7)
Аналогично определяются производные вектор-функций более высоких порядков. Производные вектор-функций порядка старше первого называются производными высших порядков.
5. Касательная к пространственной кривой определяется так же как и в случае плоской кривой. Так как производная 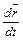 – это вектор, направленный по касательной к пространственной кривой в точке касания M (x (t 0); y (t 0); z (t 0)), то уравнения касательной к кривой
– это вектор, направленный по касательной к пространственной кривой в точке касания M (x (t 0); y (t 0); z (t 0)), то уравнения касательной к кривой 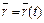 в этой точке (при t = t 0) имеют вид:
в этой точке (при t = t 0) имеют вид:
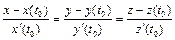 . (8)
. (8)
6. Так же как и в случае плоской кривой, прямая, перпендикулярная к касательной и проходящая через точку касания, называется нормалью к пространственной кривой в данной точке. Нормалей к данной пространственной кривой в данной точке можно провести бесчисленное множество. Все они лежат в плоскости, перпендикулярной к касательной прямой. Эта плоскость называется нормальной плоскостью. Уравнение нормальной плоскости к кривой 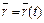 в точке t = t 0 имеет вид:
в точке t = t 0 имеет вид:
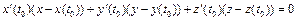 . (9)
. (9)
7. Пусть дана кривая, которая не пересекает саму себя и имеет касательную в каждой своей точке. Проведем две касательные к кривой в некоторых точках А и В и обозначим через j угол поворота касательной при переходе от точки А к точке В (рис. 4). Этот угол называется углом смежности дуги АВ. У двух дуг, имеющих одинаковую длину, больше изогнута та дуга, у которой угол смежности больше. С другой стороны, степень искривленности дуг различной длины не характеризуется только соответствующим углом смежности. Для этого используют кривизну линии, которая характеризует форму кривой, степень ее искривленности, изогнутости.
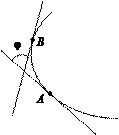 |
Рис. 4
Кривизной пространственной кривой в точке А называется предел отношения угла смежности j к длине дуги АВ = Ds, когда длина этой дуги стремится к нулю (когда точка В приближается к точке А), т. е.
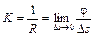 , (10)
, (10)
где величина R, обратная кривизне линии в данной точке, называется радиусом кривизны в этой точке.
Кривизна пространственной линии 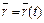 в точке t = t 0 определяется по формуле:
в точке t = t 0 определяется по формуле:
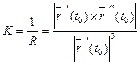 , (11)
, (11)
где 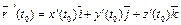 ,
, 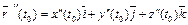 .
.
4.2. Контрольные задания
1. Дано комплексное число z. Требуется:
1) записать число z в алгебраической и тригонометрической формах;
2) найти 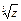 .
.
1. 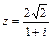 . 2.
. 2. 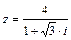 . 3.
. 3. 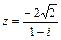 .
.
4. 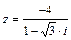 . 5.
. 5. 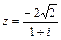 . 6.
. 6. 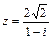 .
.
7. 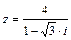 . 8.
. 8. 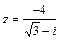 . 9.
. 9. 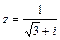 .
.
10. 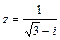 .
.
2. Найти пределы функций, не пользуясь правилом Лопиталя.
1. 1) 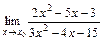 при: а)
при: а) 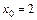 ; б)
; б) 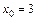 ; в)
; в) 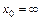 ;
;
2) 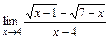 ; 3)
; 3) 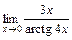 .
.
2. 1) 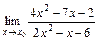 при: а)
при: а) 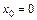 ; б)
; б) 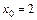 ; в)
; в) 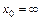 ;
;
2) 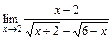 ; 3)
; 3) 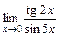 .
.
3. 1) 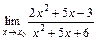 при: а)
при: а) 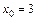 ; б)
; б) 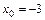 ; в)
; в) 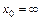 ;
;
2) 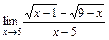 ; 3)
; 3) 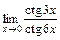 .
.
4. 1) 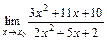 при: а)
при: а) 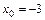 ; б)
; б) 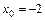 ; в)
; в) 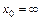 ;
;
2) 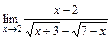 ; 3)
; 3) 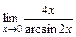 .
.
5. 1) 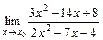 при: а)
при: а) 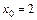 ; б)
; б) 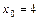 ; в)
; в) 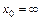 ;
;
2) 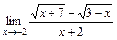 ; 3)
; 3) 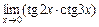 .
.
6. 1) 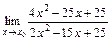 при: а)
при: а) 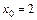 ; б)
; б) 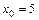 ; в)
; в) 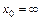 ;
;
2) 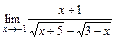 ; 3)
; 3) 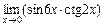 .
.
7. 1) 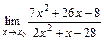 при: а)
при: а) 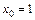 ; б)
; б) 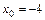 ; в)
; в) 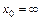 ;
;
2) 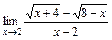 ; 3)
; 3) 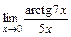 .
.
8. 1) 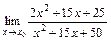 при: а)
при: а) 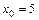 ; б)
; б) 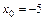 ; в)
; в) 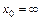 ;
;
2) 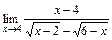 ; 3)
; 3) 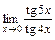 .
.
9. 1) 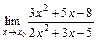 при: а)
при: а) 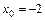 ; б)
; б) 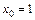 ; в)
; в) 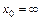 ;
;
2) 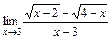 ; 3)
; 3) 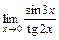 .
.
10. 1) 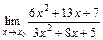 при: а)
при: а) 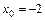 ; б)
; б) 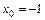 ; в)
; в) 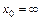 ;
;
2) 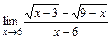 ; 3)
; 3) 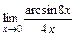 .
.
3. Задана функция y = f (x). Построить схематически график функции, вычислив пределы слева и справа в точке разрыва и предел на бесконечности.
1. 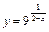 . 2.
. 2. 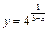 . 3.
. 3. 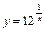 .
.
4. 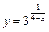 . 5.
. 5. 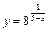 . 6.
. 6. 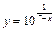 .
.
7. 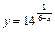 . 8.
. 8. 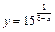 . 9.
. 9. 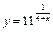 .
.
10. 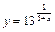 .
.
4. Найти производные 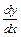 заданных функций.
заданных функций.
1. 1) 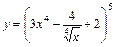 ; 2)
; 2) 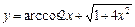 ;
;
3) 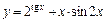 .
.
2. 1) 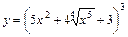 ; 2)
; 2) 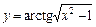 ;
;
3) 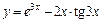 .
.
3. 1) 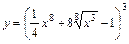 ; 2)
; 2) 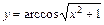 ;
;
3) 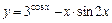 .
.
4. 1) 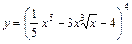 ; 2)
; 2) 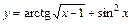 ;
;
3) 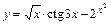 .
.
5. 1) 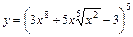 ; 2)
; 2) 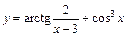 ;
;
3) 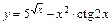 .
.
6. 1) 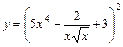 ; 2)
; 2) 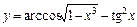 ;
;
3) 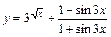 .
.
7. 1) 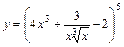 ; 2)
; 2) 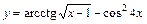 ;
;
3) 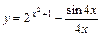 .
.
8. 1) 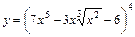 ; 2)
; 2) 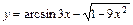 ;
;
3) 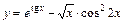 .
.
9. 1) 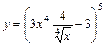 ; 2)
; 2) 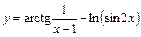 ;
;
3) 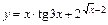 .
.
10. 1) 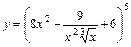 ; 2)
; 2) 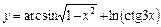 ;
;
3) 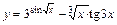 .
.
5. Найти производные 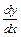 и
и 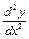 функции, заданной параметрически.
функции, заданной параметрически.
1. 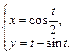 2.
2. 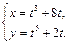 3.
3. 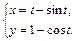
4. 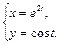 5.
5. 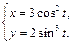 6.
6. 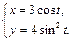
7. 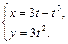 8.
8. 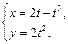 9.
9. 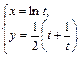
10. 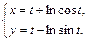
6. Провести полное исследование функции и построить ее график.
1. 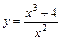 . 2.
. 2. 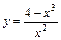 . 3.
. 3. 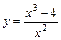 .
.
4. 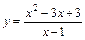 . 5.
. 5. 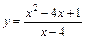 . 6.
. 6. 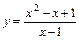 .
.
7. 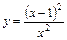 . 8.
. 8. 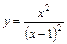 . 9.
. 9. 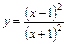 .
.
10. 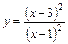 .
.
7. Найти уравнения касательной, уравнение нормальной плоскости и вычислить кривизну линии 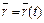 в точке t 0.
в точке t 0.
1. 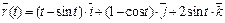 ,
, 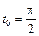 .
.
2. 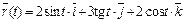 ,
, 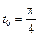 .
.
3. 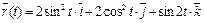 ,
, 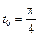 .
.
4. 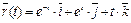 ,
, 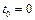 .
.
5. 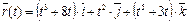 ,
, 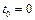 .
.
6. 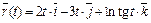 ,
, 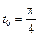 .
.
7. 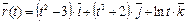 ,
, 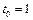 .
.
8. 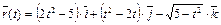 ,
, 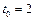 .
.
9. 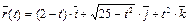 ,
, 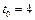 .
.
10. 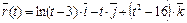 ,
, 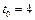 .
.
4.3. Пример решения контрольной работы
Задание 1. Дано комплексное число 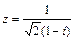 . Требуется:
. Требуется:
1) записать число z в алгебраической и тригонометрической формах;
2) найти 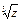 .
.
Решение. 1) Для записи комплексного числа 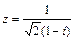 в алгебраической форме z = x + yi умножим числитель и знаменатель дроби на выражение 1 + i, сопряженное знаменателю и упростим:
в алгебраической форме z = x + yi умножим числитель и знаменатель дроби на выражение 1 + i, сопряженное знаменателю и упростим:
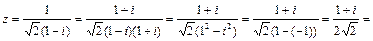
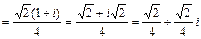 .
.
Для записи числа 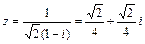 в тригонометрической форме z = r (cos j+sin j× i) найдем r и j:
в тригонометрической форме z = r (cos j+sin j× i) найдем r и j:
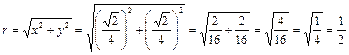 ,
,
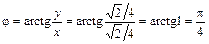 .
.
Следовательно, получим 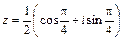 .
.
2) Воспользуемся формулой Муавра:
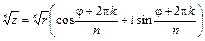 , где k = 0, 1, 2, …, n – 1.
, где k = 0, 1, 2, …, n – 1.
Полагая k = 0, 1, 2, получим:
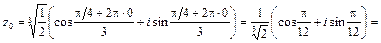
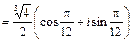 ;
;
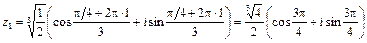 ;
;
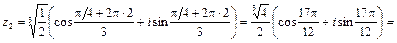
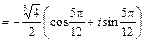 .
.
Это означает, что число 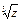 имеет три различных значения.
имеет три различных значения.
Ответ: 1) 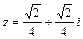 – алгебраическая форма комплексного числа,
– алгебраическая форма комплексного числа, 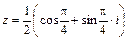 – тригонометрическая форма комплексного числа; 2)
– тригонометрическая форма комплексного числа; 2) 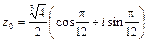 ,
, 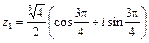 ,
,
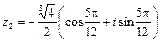 .
.
Задание 2. Найти пределы функций, не пользуясь правилом Лопиталя.
1) 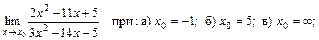
2) 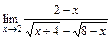 ; 3)
; 3) 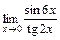 .
.
Решение. 1) Данный предел в зависимости от значений 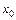 вычисляется разными способами.
вычисляется разными способами.
а)  . Найдем значения функций, стоящих в числителе и в знаменателе дроби,
. Найдем значения функций, стоящих в числителе и в знаменателе дроби, 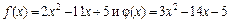 в точке
в точке  :
: 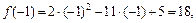
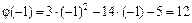 . Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке:
. Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке: 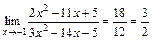 ;
;
б) 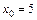 . Найдем новые значения
. Найдем новые значения 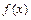 и
и 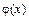 в точке
в точке 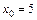 :
: 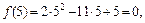
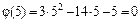 . Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке
. Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке 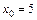 является неопределенностью вида
является неопределенностью вида 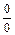 и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель
и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель 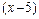 , создающий неопределенность вида
, создающий неопределенность вида 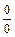 при
при 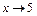 . С этой целью найдем корни уравнений
. С этой целью найдем корни уравнений 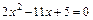 и
и 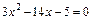 , затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель
, затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель 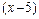 найдем предел оставшегося выражения, применяя теорему о пределе частного как в случае пункта а):
найдем предел оставшегося выражения, применяя теорему о пределе частного как в случае пункта а):
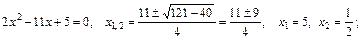
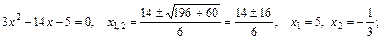
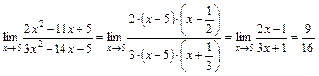 ;
;
в) 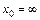 . При
. При 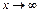 имеем
имеем 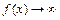 и
и 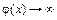 , т. е. заданное отношение при
, т. е. заданное отношение при 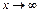 является неопределенностью вида
является неопределенностью вида 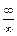 и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной
и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной 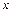 . В данном случае это есть
. В данном случае это есть 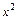 . После сокращения дроби на критический множитель
. После сокращения дроби на критический множитель 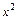 применим теорему о пределе частного и следующие равенства, известные из теории пределов:
применим теорему о пределе частного и следующие равенства, известные из теории пределов: 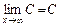 ,
, 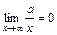 ,
, 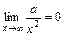 .
.
Получим:
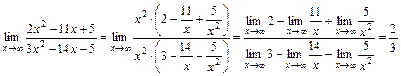 .
.
2) Найдем значения функций 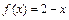 и
и 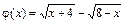 , стоящих в числителе и знаменателе дроби, в точке
, стоящих в числителе и знаменателе дроби, в точке 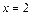 :
: 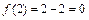 ,
, 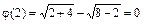 . Следовательно, заданное отношение
. Следовательно, заданное отношение 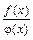 при
при 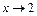 является неопределенностью вида
является неопределенностью вида 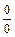 . Для нахождения предела отношения выделим в числителе и в знаменателе критический множитель
. Для нахождения предела отношения выделим в числителе и в знаменателе критический множитель 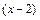 , создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю
, создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю 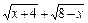 и используем формулу сокращенного умножения разности квадратов:
и используем формулу сокращенного умножения разности квадратов: 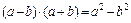 :
:
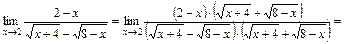

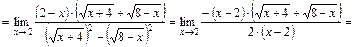
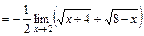 .
.
По теореме о пределе корня 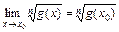 , получим:
, получим:
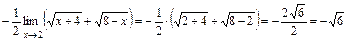 .
.
3) 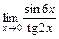 . Найдем значения функций
. Найдем значения функций 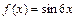 и
и 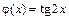 в точке
в точке 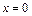 :
: 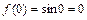 и
и 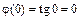 . Следовательно, заданное отношение представляет собой при
. Следовательно, заданное отношение представляет собой при 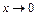 неопределенность вида
неопределенность вида 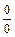 . Вычислим этот предел, применяя формулу первого замечательного предела:
. Вычислим этот предел, применяя формулу первого замечательного предела: 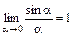 и равенство
и равенство 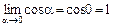 , вытекающее из непрерывности в точке
, вытекающее из непрерывности в точке 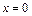 функции
функции 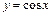 . С этой целью преобразуем заданный предел следующим образом:
. С этой целью преобразуем заданный предел следующим образом:
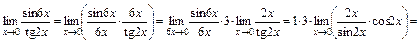
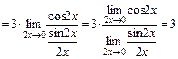 .
.
Ответ: 1), а) 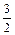 ; б)
; б) 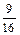 ; в)
; в) 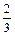 . 2)
. 2) 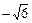 . 3) 3.
. 3) 3.
Задание 3. Задана функция 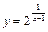 . Построить схематически график функции, вычислив пределы слева и справа в точке разрыва и предел на бесконечности.
. Построить схематически график функции, вычислив пределы слева и справа в точке разрыва и предел на бесконечности.
Решение. Рассмотрим точку х = 1. Найдем пределы слева и справа функции в данной точке:
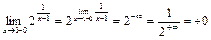 ,
,
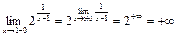 .
.
Так как предел справа равен бесконечности, то х = 1 – точка разрыва второго рода.
Предел функции на бесконечности равен:
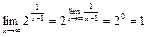 .
.
Строим схематически график функции 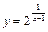 , используя полученные результаты (рис. 5).
, используя полученные результаты (рис. 5).
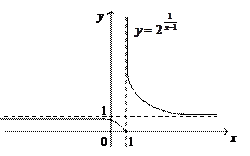
Рис. 5
Задание 4. Найти производные 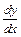 заданных функций.
заданных функций.
1) 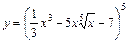 ; 2)
; 2) 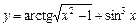 ;
;
3) 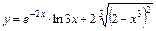 .
.
Решение. 1) 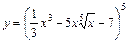 .
.
Используем правило дифференцирование суммы 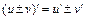 и правила дифференцирования сложной функции вида
и правила дифференцирования сложной функции вида 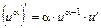 , где
, где 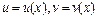 , а также таблицу производных. Получим:
, а также таблицу производных. Получим:
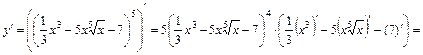
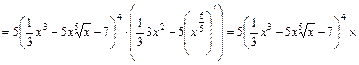
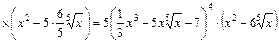 .
.
2) 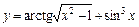 .
.
Используем правило дифференцирование суммы 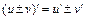 и правила дифференцирования сложных функций вида
и правила дифференцирования сложных функций вида
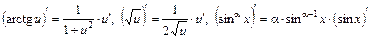 ,
,
где 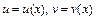 , а также таблицу производных. Получим:
, а также таблицу производных. Получим:
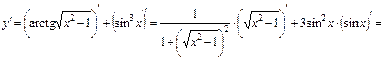
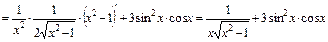 .
.
3) 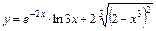 .
.
Используем правило дифференцирования суммы 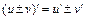 , правило дифференцирования произведения
, правило дифференцирования произведения 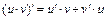 и правила дифференцирования сложных функций вида
и правила дифференцирования сложных функций вида
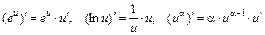 ,
,
где 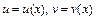 , а также таблицу производных. Получим:
, а также таблицу производных. Получим:
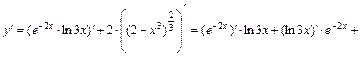
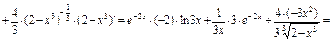
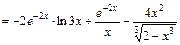 .
.
Ответ: 1) 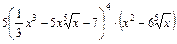 ; 2)
; 2) 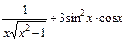 ; 3)
; 3) 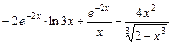 .
.
Задание 5. Найти производные 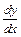 и
и 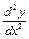 функции
функции 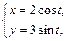 заданной параметрически.
заданной параметрически.
Решение. Производная 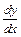 функции
функции 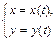 , заданной параметрически, вычисляется по формуле:
, заданной параметрически, вычисляется по формуле:
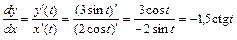 .
.
Вторую производную найдем по формуле:
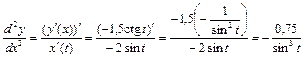 .
.
Ответ: 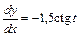 ,
, 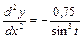 .
.
Задание 6. Провести полное исследование функции 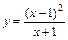 и построить ее график.
и построить ее график.
Решение. 1) Найдем область определения, интервалы непрерывности и точки разрыва функции.
Функция определена на всей числовой оси, кроме точки 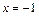 , т. е.
, т. е. 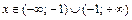 . В каждой точке области определения функция непрерывна. Точка
. В каждой точке области определения функция непрерывна. Точка 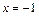 есть точка разрыва функции, т. к. знаменатель функции в этой точке равен нулю, а числитель отличен от нуля.
есть точка разрыва функции, т. к. знаменатель функции в этой точке равен нулю, а числитель отличен от нуля.
2) Выясним четность, нечетность и периодичность функции.
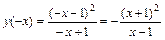 , т. е.
, т. е. 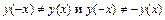 . Следовательно, функция не является ни четной, ни нечетной.
. Следовательно, функция не является ни четной, ни нечетной.
Функция непериодична, т. к. 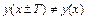 , где Т – некоторое действительное число.
, где Т – некоторое действительное число.
3) Найдем асимптоты графика функции (вертикальные, горизонтальные и наклонные):
|
Так как точка 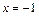 оси Ox есть точка разрыва функции, то прямая линия
оси Ox есть точка разрыва функции, то прямая линия 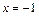 , перпендикулярная оси Ox, есть вертикальная асимптота графика. Исследуем поведение графика функции вблизи вертикальной асимптоты по односторонним пределам функции. Возьмем слева от точки
, перпендикулярная оси Ox, есть вертикальная асимптота графика. Исследуем поведение графика функции вблизи вертикальной асимптоты по односторонним пределам функции. Возьмем слева от точки 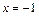 близкое значение, например,
близкое значение, например, 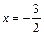 и вычислим в нем значение функции и ее знак:
и вычислим в нем значение функции и ее знак:
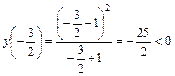 .
.
Так как это значение отрицательно, и функция слева от точки 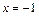 непрерывна, то она сохраняет знак и
непрерывна, то она сохраняет знак и 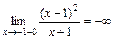 .
.
Теперь возьмем справа от точки 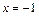 близкое значение, например,
близкое значение, например, 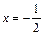 :
:
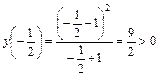 .
.
Так как это значение положительно, и функция справа от точки 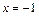 непрерывна, то при переходе к пределу функция сохраняет знак и
непрерывна, то при переходе к пределу функция сохраняет знак и 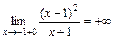 .
.
Таким образом, слева от точки 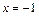 функция отрицательна, а справа от точки
функция отрицательна, а справа от точки 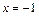 – положительна и имеет односторонние пределы, равные бесконечности. Такая точка называется точкой разрыва второго рода (или точкой бесконечного разрыва функции);
– положительна и имеет односторонние пределы, равные бесконечности. Такая точка называется точкой разрыва второго рода (или точкой бесконечного разрыва функции);
б) Горизонтальные асимптоты.
Для нахождения горизонтальной асимптоты нужно найти предел функции при 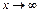 , раскрывая неопределенность вида
, раскрывая неопределенность вида 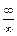 . Если существует конечный предел
. Если существует конечный предел 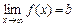 , то прямая, определяемая уравнением
, то прямая, определяемая уравнением 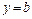 , есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:
, есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:
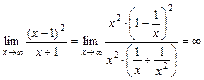 .
.
Предел равен бесконечности, значит горизонтальной асимптоты нет;
в) Наклонные асимптоты.
Наклонная асимптота имеет уравнение прямой линии с угловым коэффициентом вида 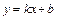 , где
, где 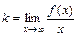 ,
, 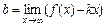 . Если
. Если 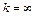 , то наклонной асимптоты не существует.
, то наклонной асимптоты не существует.
Найдем оба указанных предела для заданной функции:
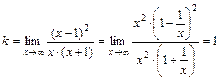 ,
,
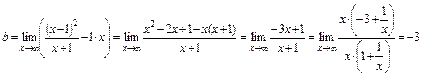 .
.
Таким образом, график имеет наклонную асимптоту 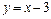 .
.
4) Найдем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции.
Находим сначала первую производную функции:
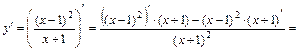
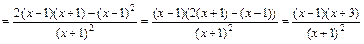 .
.
Так как точка 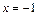 , в которой
, в которой 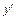 не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых
не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых 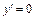 или
или 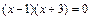 , т. е.
, т. е. 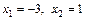 .
.
Критические точки и точка разрыва 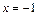 разбивают ось Ox на 4 интервала монотонности функции. По знаку производной
разбивают ось Ox на 4 интервала монотонности функции. По знаку производной 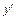 в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в табл. 1.
в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в табл. 1.
Таблица 1
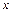
| 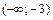
| 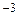
| 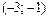
| 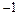
| 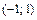
| 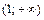
| |
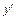
| + | – | не сущ. | – | + | ||
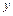
| ä | –8 max | æ | не сущ. | æ | min | ä |
5) Найдем интервалы выпуклости и вогнутости графика функции, точки перегиба.
Находим сначала вторую производную функции:
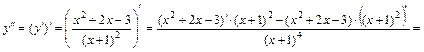
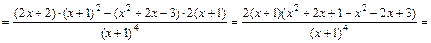
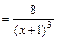 .
.
Так как точка 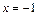 не принадлежит области определения функции и
не принадлежит области определения функции и 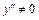 , то критических точек второго рода нет.
, то критических точек второго рода нет.
Точка разрыва разбивают числовую ось Ox на 2 интервала, в которых по знаку второй производной 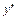 определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.
определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.
Таблица 2
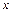
| 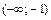
| 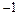
| 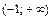
|
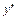
| – | не сущ. | + |
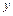
| Ç выпуклый | не сущ. | È вогнутый |
6) Находим точки пересечения графика функции с осями координат, решая две системы уравнений.
С осью Ox: 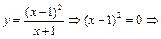 А (1; 0) – точка пересечения графика с осью Ox.
А (1; 0) – точка пересечения графика с осью Ox.
С осью Oy: 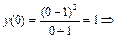 В (0; 1) – точка пересечения графика с осью Oу.
В (0; 1) – точка пересечения графика с осью Oу.
7) Используя результаты исследования, строим график функции в такой последовательности: а) строим вертикальную асимптоту 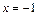 и наклонную асимптоту
и наклонную асимптоту 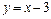 , подписываем их; б) изображаем максимум функции в точке
, подписываем их; б) изображаем максимум функции в точке 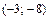 и минимум в точке
и минимум в точке 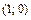 ; в) наносим на осях точки А (1; 0) и В (0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот (рис. 6).
; в) наносим на осях точки А (1; 0) и В (0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот (рис. 6).
Задание 7. Найти уравнения касательной, уравнение нормальной плоскости и вычислить кривизну линии 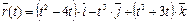 в точке t 0 = 1.
в точке t 0 = 1.
Решение. 1)Для составления уравнений касательной в точке t 0 = 1 воспользуемся формулой 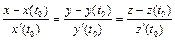 . Имеем:
. Имеем:
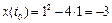 ,
, 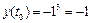 ,
, 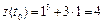 ;
;
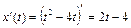 ,
, 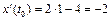 ;
;
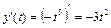 ,
, 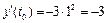 ;
;
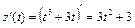 ,
, 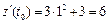 .
.
Таким образом, получим: 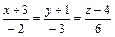 .
.
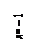  |
Рис. 6
2) Запишем уравнение нормальной плоскости в точке t 0 = 1 по формуле 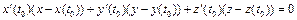 и упростим:
и упростим:
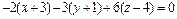 или
или 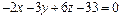 или
или 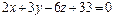 .
.
3) Для нахождения кривизны линии в точке t 0 = 1 применим формулу 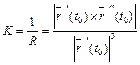 , где
, где 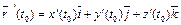 ,
, 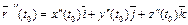 . Имеем:
. Имеем:
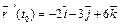 ;
;
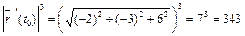 ;
;
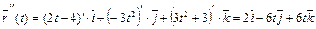 ,
,
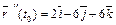 ;
;
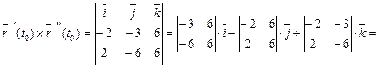
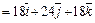 ,
,
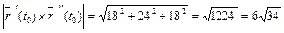 .
.
Таким образом, окончательно получим: 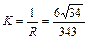 .
.
Ответ: 1) 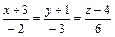 – уравнения касательной в точке t 0 = 1; 2)
– уравнения касательной в точке t 0 = 1; 2) 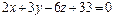 – уравнение нормальной плоскости в точке t 0 = 1.
– уравнение нормальной плоскости в точке t 0 = 1.
4.4. Вопросы для самопроверки
1. Основные понятия о комплексных числах. Геометрическое изображение комплексного числа. Тригонометрическая и показательная формы записи комплексных чисел.
2. Действия над комплексными числами в алгебраической форме.
3. Действия над комплексными числами в тригонометрической форме. Формулы Муавра.
4. Действия над комплексными числами в показательной форме.
5. Предел переменной. Окрестность точки. Предел функции в точке и на бесконечности. Односторонние пределы.
6. Бесконечно малые и бесконечно большие функции, ограниченные функции. Их свойства.
7. Основные теоремы о пределах функций. Неопределенности.
8. Теорема о сжатой функции. Первый замечательный предел.
9. Основные понятия о числовых последовательностях.
10. Число е. Второй замечательный предел.
11. Непрерывность функции в точке. Точки разрыва. Свойства непрерывных функций.
12. Свойства функций непрерывных на отрезке.
13. Определение производной функции в точке и на интервале.
14. Геометрический и механический смысл производной.
15. Дифференцируемость и непрерывность функций. Дифференциал функции.
16. Формулы и правила дифференцирования функций.
17. Дифференцирование сложной функции, неявной функции и функции, заданной параметрически.
18. Производные и дифференциалы высших порядков.
19. Экстремум функции. Необходимые и достаточные условия экстремума.
20. Выпуклость и вогнутость графика функции. Точки перегиба.
21. Асимптоты графика функции.
22. Наибольшее и наименьшее значения функции на отрезке.
23. Полное исследование функции и построение ее графика.
24. Понятие вектор-функции скалярного аргумента.
25. Как определяется предел и производная вектор-функции скалярного аргумента?
26. Понятие кривизны плоской линии. Формула для ее вычисления.
27. Касательная и нормальная плоскость пространственной линии в точке. Их уравнения.
Список литературы
1. Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу [и др.]. – М.: Рольф, 2001. – 576 с.
2. Методические указания для студентов специальности 060800 «Экономика и управление на предприятии (строительство)» заочной формы обучения по дисциплине «Высшая математика» / ВИСТех (филиал) ВолгГАСУ; [сост. Е.В. Абрамов, Е.Д. Илларионова, Е.Ю. Волченко]. – Волжский: ВИСТех (филиал) ВолгГАСУ, 2010. – 95 с.
3. Письменный, Д. Т. Конспект лекций по высшей математике. 1 часть. / Д. Т. Письменный. – М.: Рольф, 2001. – 288 с.
4. Рябушко, А. П. Сборник индивидуальных заданий по высшей математике. Часть 1 / А. П. Рябушко [и др.]. – Мн.: Выш. шк., 1992
План уч.-метод. докум. 2012 г., поз. № 20
Дата публикования: 2014-11-18; Прочитано: 2288 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!