Эвристический метод решения задачи булева программирования

Существует два метода решения задач с булевыми переменными.

Во-первых, их можно решать как обычные задачи целочисленного программирования, т. е. методом ветвей и границ. При этом на каждую переменную накладывается два требования: они должны быть в пределах 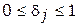; 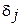должны быть целыми. Совершенно очевидно, что выполнение этих двух требований обеспечивает получение в решении значений 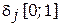, т. е. равных либо 0, либо 1.

Вторым методом является метод сплошного перебора. Посмотрим его на таком примере. Пусть требуется решить систему:

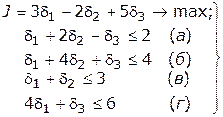
(1)

Поскольку 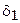, , 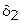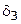могут принимать значения 0 или 1 в любом сочетании, рассмотрим все возможные сочетания, как это сделано в табл. 3.8.1. Работа при полном переборе выполняется в такой последовательности.

1. Заполнить все возможные варианты сочетаний допустимых значений , , .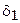

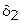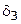2. Определить значения левых частей ограничений (1)–(4) и целевой функции и записать их.

Таблица 3.8.1.

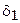
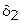
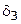
Вариант				(а)	(б)	(в)	(г)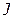
								–2
				–1
Требование	£2	£4	£3	£6	max

3. Вычеркнуть те варианты, в которых не удовлетворяется хотя бы одно ограничение. В примере ограничение (а) не удовлетворяется в четвертом варианте; ограничение (2) — в четвертом, седьмом и восьмом, которые таким образом, вычеркиваются как приводящие к недопустимым решениям.

4. Из оставшихся вариантов принимается тот, в котором целевая функция приобретает максимальное значение. В примере оно равно 8; при этом оптимальный вариант — шестой, в котором ; ; ; .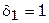

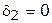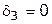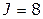Из рассмотренного примера видно, что в данном случае всего вариантов будет 2³=8 и для каждого варианта надо вычислить четыре ограничения и целевую функцию, т. е. выполнить 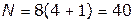вычислительных операций. В общем случае число вычислительных процедур при полном переборе

,

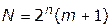где 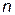— число переменных; — число ограничений. Число вычислительных процедур для некоторых значений и приведено в табл. 3.8.2, из которой видно, как резко увеличивается число вариантов, которые надо вычислить при увеличении размерности решаемой задачи.

Таблица 3.8.2.

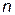
Для сокращения трудоемкости, необходимой при полном переборе, были предложены различные методы. Рассмотрим один из них, в котором работу производят в такой последовательности.

1. Принять некоторые значения 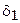, , 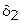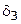. Для конкретности изложения принимает ; .

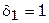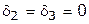2. Определить значение целевой функции при таком наборе переменных

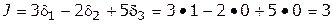
Значит, при принятом наборе переменных целевая функция 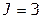. Поэтому не будем рассматривать варианты, в которых целевая функция принимает меньшие значения. Для этого вводим дополнительное ограничение

,

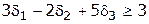(Ф)

которые будем называть фильтром.

3. Составить табл. 3.8.3.

4. Проверить для каждого варианта выполнение ограничений. Вычисление для каждого варианта прекращать в том случае, если будет не выполнено хотя бы одно ограничение, включая фильтр. Если вычисление прекращается и величины не определены, то в клетках табл. 3.8.3 ставится прочерк. Введение фильтрующего ограничения (Ф) привело в тому, что в табл. 3.8.3 вычислены 24 величины вместо 40 при полном переборе, что составило 60%.

Таблица 3.8.3.

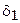
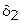
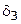
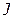
Номер варианта					(а)	(б)	(в)	(г)
					—	—	—	—
				–2	—	—	—	—
					—	—	—	—
					–1
							—	—
							—	—
Требование	³3	£2	£4	£3	£6

Число вычислений можно еще уменьшить, если фильтр иметь не постоянный для всего цикла вычислений, а изменяющийся. Напомним, что в качестве фильтра было принято значение целевой функции при некотором наборе переменных, т. е. некоторое допустимое решение. Если в ходе вычислений при каком-либо наборе переменных значение целевой функции окажется лучше, чем у фильтра, то это новое лучшее допустимое решение следует принять для следующих вычислений в качестве нового фильтра. Такой фильтр называют адаптивным. Покажем, как вести вычисления с помощью адаптивного фильтра. Из табл. 3.8.3 видно, что в пятом варианте 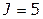. Поэтому для дальнейших вычислений в качестве фильтрующего ограничения принимаем ограничение

.

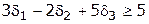(Ф-1)

Однако для следующего варианта целевая функция будет уже больше и равна.

Значит, в качестве фильтрующего принимаем опять новое ограничение

.

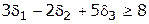(Ф-2)

Для седьмого и восьмого вариантов, для которых целевая функция не удовлетворяет требованиям фильтра (Ф-2), значения ограничений не вычисляем. Значит, благодаря трехкратному введению фильтров мы сократили число величин, для которых надо производить вычисления, еще на 4. Итого надо выполнить 20 вычислений вместо 40 при полном переборе, т. е. в 2 раза меньше.

Есть методы, с помощью которых наибольшее значение фильтра можно получить на первых вариантах расчета. Тогда сокращение трудоемкости при вычислениях будет еще более значительным. Такой современный метод называют методом Баллаша с фильтром.