 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Проверка количественных характеристик выборки
|
|
В §1 были определены характеристики генеральной совокупности, т.е. принадлежность к одной генеральной выборке, а также среднее и первый момент.
На данном этапе имеется функция распределения, которая визуально похожа на некоторое уже известное распределение. Но необходимо описать эту близость математически.
Итак, начнем с рассмотрения критериев согласия.
Критерий Согласия применяется в задаче проверки согласия, суть которой заключается в следующем. Пусть X1, Х2,..., Хn -независимые случайные величины, подчиняющиеся одному и тому же вероятностному закону, функция распределения которого F(x) неизвестна. В таком случае задача статистической проверки гипотезы Н0, согласно которой F(x) = F0(x), где F0(x) - некоторая заданная функция распределения, называемая задачей проверки согласия. Например, если F0(x) - непрерывная функция распределения, то в качестве критерия согласия для проверки гипотезы Н0 можно воспользоваться критерием Колмогорова или Смирного.
Предположим, что выборка 
 произведена из генеральной совокупности с неизвестной теоретической функцией распределения, относительно которой имеются две непараметрические гипотезы: простая основная
произведена из генеральной совокупности с неизвестной теоретической функцией распределения, относительно которой имеются две непараметрические гипотезы: простая основная 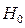 : F(x) = F0(x) и сложная конкурирующая
: F(x) = F0(x) и сложная конкурирующая 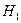 : F
: F 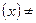 F
F 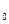
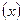
 , где F
, где F 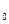 (x) — известная функция распределения. Иными словами, мы хотим проверить, согласуются эмпирические данные с нашим гипотетическим предположением относительно теоретической функции распределения или нет. Поэтому критерии для проверки гипотез Н
(x) — известная функция распределения. Иными словами, мы хотим проверить, согласуются эмпирические данные с нашим гипотетическим предположением относительно теоретической функции распределения или нет. Поэтому критерии для проверки гипотез Н 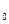 и Н
и Н 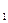 носят название критериев согласия.
носят название критериев согласия.
Пример. Гипотезу о том, что числа 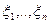 представляют собой независимые значения случайной величины, равномерно распределенной на отрезке
представляют собой независимые значения случайной величины, равномерно распределенной на отрезке 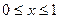 , можно проверять с помощью критерия Колмогорова, основанного на статистике
, можно проверять с помощью критерия Колмогорова, основанного на статистике
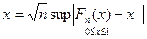 ,
,
где 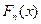 - эмпирическая функция распределения выборки
- эмпирическая функция распределения выборки 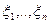 . Соответствующая детерминистическая задача: можно ли с заданной точностью оценить интеграл произвольной функции f(x) из
. Соответствующая детерминистическая задача: можно ли с заданной точностью оценить интеграл произвольной функции f(x) из  , усредняя значения
, усредняя значения 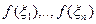 . Формула
. Формула
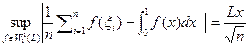
показывает, что это возможно тогда и только тогда, когда величина х достаточно мала.
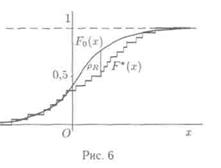
Критерий согласия Колмогорова. Уже говорилось (параграф 3 гл. 1), что в силу теоремы Гливенко-Кантелли эмпирическая функция распределения F*(x) представляет собой состоятельную оценку теоретической функции распределения F(x). Поэтому можно сравнить эмпирическую функцию распределения F*(x) с гипотетической F0(x) и, если мера расхождения между ними мала, то считать справедливой гипотезу H0.
|
Наиболее естественной и простой из таких мер (будем предполагать, что F 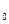 (x) — непрерывная функция) является равномерное расстояние
(x) — непрерывная функция) является равномерное расстояние
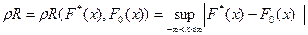
(рис. 6). Однако при построении критерия
Колмогорова более удобно пользоваться нормированным расстоянием 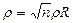 .
.
Итак, рассмотрим статистику

Критерий Колмогорова предписывает принять гипотезу H0, если 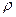 <С, и отвергнуть в противном случае, где С — критическое значение критерия.
<С, и отвергнуть в противном случае, где С — критическое значение критерия.
Если гипотеза H 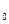 справедлива, то распределение статистики
справедлива, то распределение статистики 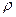 не зависит от гипотетической функции распределения F0(x) (доказательство этого факта следует из инвариантности статистики критерия Колмогорова относительно монотонных преобразований, в частности преобразования g(x)=F
не зависит от гипотетической функции распределения F0(x) (доказательство этого факта следует из инвариантности статистики критерия Колмогорова относительно монотонных преобразований, в частности преобразования g(x)=F 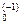 (x), где F
(x), где F 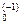 (x) — обратная к F
(x) — обратная к F 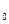 (x) функция; преобразование g(х) приводит выборку Х
(x) функция; преобразование g(х) приводит выборку Х 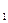 ,...,Х
,...,Х 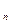 к равномерно распределенной на отрезке (0,1)). Поэтому можно рассчитать таблицы, которые по заданному объему выборки и и критическому значению С позволяют определить уровень значимости критерия а. Поскольку на практике обычно, наоборот, считают известными уровень значимости а и объем выборки п, а затем по ним определяют критическое значение С.
к равномерно распределенной на отрезке (0,1)). Поэтому можно рассчитать таблицы, которые по заданному объему выборки и и критическому значению С позволяют определить уровень значимости критерия а. Поскольку на практике обычно, наоборот, считают известными уровень значимости а и объем выборки п, а затем по ним определяют критическое значение С.
При 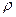 —>
—> 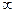 распределение статистики
распределение статистики 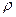 сходится к распределению Колмогорова [1, табл. 6.1], и критическое значение С при большом объеме выборки практически совпадает с (1-
сходится к распределению Колмогорова [1, табл. 6.1], и критическое значение С при большом объеме выборки практически совпадает с (1- 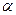 )-квантилью
)-квантилью 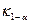 распределения Колмогорова.
распределения Колмогорова.
При практической реализации критерия Колмогорова сначала по выборке Х 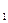 ,...,Х
,...,Х 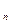 составляют вариационный ряд Х
составляют вариационный ряд Х 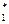 ,…,Х
,…,Х 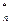 . Затем находят F
. Затем находят F 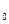 (X
(X 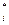 ) и определяют значения статистики р по формуле
) и определяют значения статистики р по формуле

Наконец, сравнивают полученное значение 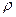 с критическим значением С для заданного уровня значимости
с критическим значением С для заданного уровня значимости 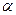 и принимают или отвергают гипотезу H
и принимают или отвергают гипотезу H 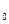 .
.
Пример. Проверим с помощью критерия Колмогорова гипотезу Н 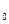 о том, что проекция X вектора скорости молекулы водорода на ось координат (см. пример 1 из гл. 1) распределена по нормальному закону. Проверку произведем для уровня значимости
о том, что проекция X вектора скорости молекулы водорода на ось координат (см. пример 1 из гл. 1) распределена по нормальному закону. Проверку произведем для уровня значимости 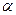 = 0,05. Параметры нормального закона не заданы, значит, мы имеем дело со сложной гипотезой Н
= 0,05. Параметры нормального закона не заданы, значит, мы имеем дело со сложной гипотезой Н 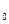 и сначала должны оценить среднее
и сначала должны оценить среднее 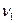 и дисперсию
и дисперсию  - Поскольку мы будем пользоваться критерием Колмогорова, хотелось бы оценки
- Поскольку мы будем пользоваться критерием Колмогорова, хотелось бы оценки 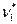 и
и 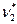 неизвестных параметров
неизвестных параметров 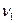 и
и  выбрать таким образом, чтобы они доставляли минимальное значение статистики критерия Колмогорова
выбрать таким образом, чтобы они доставляли минимальное значение статистики критерия Колмогорова
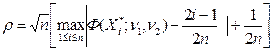
где 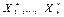 — вариационный ряд выборки
— вариационный ряд выборки  , приведенный в табл. 3 гл. 1, а
, приведенный в табл. 3 гл. 1, а 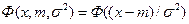 — функция распределения
— функция распределения
нормального закона с параметрами 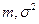 . Однако искать минимум
. Однако искать минимум 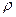
как функции от 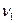 и
и  — весьма сложная в вычислительном плане
— весьма сложная в вычислительном плане
задача, так как Ф(х) даже не выражается в элементарных функциях-
Поэтому в качестве оценок 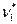 и
и 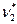 используем оценки максимального правдоподобия
используем оценки максимального правдоподобия 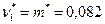 и
и 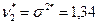 (см. примеры 8 из гл. 1 и 15 из гл.2). Теперь с помощью критерия Колмогорова будем проверять простую гипотезу
(см. примеры 8 из гл. 1 и 15 из гл.2). Теперь с помощью критерия Колмогорова будем проверять простую гипотезу 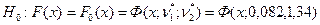 . Вычислив сначала
. Вычислив сначала 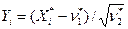 и воспользовавшись равенством
и воспользовавшись равенством 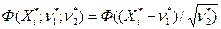 последовательно находим затем значения
последовательно находим затем значения 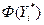 (1, c. 112-117),
(1, c. 112-117), 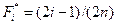 b
b 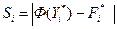 (табл.2). Наконец, определяя значение статистики критерия Колмогорова
(табл.2). Наконец, определяя значение статистики критерия Колмогорова
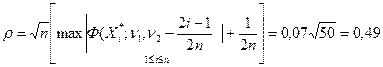
(максимальное значение 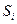 равно 0,06) и сравнивая его с 0,95-квантилью распределения Колмогорова
равно 0,06) и сравнивая его с 0,95-квантилью распределения Колмогорова 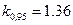 , видим, что
, видим, что 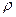 <
< 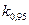 .Значит, мы должны принять гипотезу Н
.Значит, мы должны принять гипотезу Н 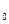 и считать распределение проекции вектора скорости молекулы водорода нормальным.
и считать распределение проекции вектора скорости молекулы водорода нормальным.
Критерий Шапиро-Уилка. Базируется на анализе линейной комбинации разностей порядковых статистик, используют при объемах выборки 8£ 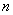 £50. Рекомендуют применять при отсутствии априорной информации о типе возможного отклонения от нормальности. Критерий Шапиро-Уилкаhttp://www.ami.nstu.ru/%7Eheadrd/Kurs_projekt.htm - _ftn5 используют в тех случаях, когда в качестве альтернативы можно выбрать гипотезу следующего вида: примерно симметричное распределение с
£50. Рекомендуют применять при отсутствии априорной информации о типе возможного отклонения от нормальности. Критерий Шапиро-Уилкаhttp://www.ami.nstu.ru/%7Eheadrd/Kurs_projekt.htm - _ftn5 используют в тех случаях, когда в качестве альтернативы можно выбрать гипотезу следующего вида: примерно симметричное распределение с 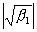 <1/2 и
<1/2 и 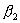 <3 или асимметричное распределение (например,
<3 или асимметричное распределение (например, 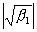 >1/2). В противном случае рекомендуют критерий Эппса-Палли. Для вариационного ряда
>1/2). В противном случае рекомендуют критерий Эппса-Палли. Для вариационного ряда 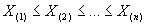 , построенного по наблюдаемой выборке
, построенного по наблюдаемой выборке 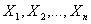 , вычисляют величину
, вычисляют величину
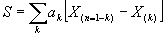 (159)
(159)
где индекс  изменяется от 1 до
изменяется от 1 до 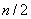 или от 1 до
или от 1 до 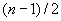 при четном и нечетном
при четном и нечетном 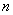 соответственно. Статистика критерия имеет вид
соответственно. Статистика критерия имеет вид
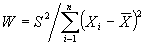 . (160)
. (160)
Гипотеза о нормальности отвергается при малых значениях статистики 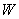 .
.
Критерий Эппса-Палли. Базируется на сравнении эмпирической и теоретической характеристических функциях, применяют при 8 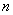 200. По наблюдаемой выборке
200. По наблюдаемой выборке 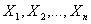 вычисляют статистику критерия
вычисляют статистику критерия
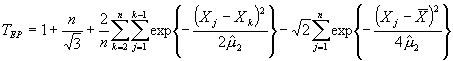 , (161)
, (161)
где 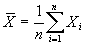 ,
, 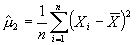 .
.
Гипотезу о нормальности отвергают при больших значениях статистики.
Модифицированный критерий Шапиро-Уилка. Применяется для нескольких независимых выборок одинакового объема 8 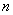 50, когда отдельная выборка слишком мала, чтобы обнаружить отклонения от нормальности. Предполагается, что
50, когда отдельная выборка слишком мала, чтобы обнаружить отклонения от нормальности. Предполагается, что 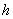 выборок одного и того же объема
выборок одного и того же объема 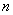 взято из одной генеральной совокупности. Для каждой выборки в соответствии с соотношением (160) подсчитывают значения
взято из одной генеральной совокупности. Для каждой выборки в соответствии с соотношением (160) подсчитывают значения 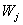 ,
, 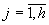 . Вычисляют значения
. Вычисляют значения
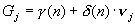 , (161)
, (161)
где
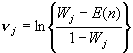 , (162)
, (162)
а коэффициенты 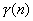 ,
, 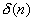 и
и 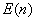 табулированы. Если наблюдаемое распределение нормальное, то переменные
табулированы. Если наблюдаемое распределение нормальное, то переменные 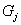 приблизительно подчиняются стандартному нормальному закону. В качестве статистики критерия используется величина
приблизительно подчиняются стандартному нормальному закону. В качестве статистики критерия используется величина
 , (163)
, (163)
где
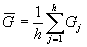 . (164)
. (164)
Гипотеза  о нормальности отклоняется, при уровне значимости
о нормальности отклоняется, при уровне значимости 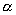 , если
, если
 <
<  , (165)
, (165)
где  – соответствующий квантиль стандартного нормального распределения.
– соответствующий квантиль стандартного нормального распределения.
Список литературы
1. Лемешко Б.Ю., Помадин С.С. Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального // Метрология. 2004. – № 3.- С.3-15.
2. Лемешко Б.Ю., Лемешко С.Б., Миркин Е.П. Исследование критериев проверки гипотез, используемых в задачах управления качеством // Материалы VII международной конференции “Актуальные проблемы электронного приборостроения” АПЭП-2004. Новосибирск, 2004. – Т. 6. – С. 269-272.
3. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
4. Лемешко Б.Ю., Миркин Е.П. Критерии Бартлетта и Кокрена в измерительных задачах при вероятностных законах, отличающихся от нормального // Измерительная техника. 2004. № 10. – С. 10-16.
5. Орлов А.И. О проверке однородности двух независимых выборок // Заводская лаборатория. – 2003. – Т.69. №.1. – С.55-60.
6. Смирнов Н.В. Оценка расхождения между эмпирическими кривыми распределения в двух независимых выборках // Бюллетень МГУ, серия А. – 1939. – Т.2. №2. – С.3-14.
7. Боровков А.А. К задаче о двух выборках // Изв. АН СССР, серия матем., 1962. Т. 26. – С.605-624.
8. Королюк В.С. Асимптотический анализ распределений максимальных уклонений в схеме Бернулли // Теория вероятностей и ее применения. – 1959. – Т.4. – С. 369-397.
9. Смирнов Н.В. Вероятности больших значений непараметрических односторонних критериев согласия // Труды Матем. ин-та АН СССР. – 1961. – Т.64. – С. 185-210.
10. Lehmann E.L. Consistency and unbiasedness of certain nonparametric tests / Ann. Math. Statist. – 1951. V.22. № 1. – P.165-179.
11. Rosenblatt M. Limit theorems associated with variants of the von Mises statistic // Ann. Math. Statist. – 1952. V.23. – P.617-623.
12. Энциклопедический словарь Вероятность и математическая статистика.
13. А.Н. Ширяев Вероятность // Изд. МЦНМО – 2004. – Ч1. – С. 448-490.
Кластерный анализ
Дата публикования: 2014-11-18; Прочитано: 1395 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
