Метод. Метод минимизирующих карт Карно

внимания …………………………………………………………………..54

Методика 7.1. Сложение чисел с переключением……………….…..55

Методика 7.2. Отыскивание чисел с переключением………………..59

Методика 7.3. Распределение и переключение внимания…………...64

Методика 7.4. Тест К.К. Платонова…………………………………...66

Литература ………………………………………………………………...70

Л.С. Тихомирова

МЕТОДЫ

минимизации булевых функций

Прогресс во многих областях человеческой деятельности связан с решением проблем автоматизации процессов обработки и преобразования информации. Математическими носителями информации являются сигналы.

Способ преобразования информации любой физической системой характеризуется законом функционирования системы. Удобно кодировать информацию (отвлекаясь от ее характера и смысла) конечным набором символов (букв).

Законы функционирования системы описываются логическими функциями (булевыми функциями). Один и тот же закон можно реализовать функциями, имеющими различное число знаков, соединенных различными логическими операциями.

Любая булева функция может быть записана в фиксированном виде (СДНФ или СКНФ), но эта запись не экономна. Проблема простейшего представления функции сводится к проблеме выбора базиса и проблеме наиболее экономного представления функции в этом базисе. Это и есть проблема минимизации функции.

В настоящее время наибольшее распространение получил базис, состоящий из инверсии, конъюнкции и дизъюнкции (‾, Ù, Ú). Образующие его функции наиболее просты с точки зрения математических преобразований и технической реализации, кроме того, от них легко перейти в любой другой базис.

Минимизация функций проводится обычно в классе ДНФ, но возможна и в КНФ. В основу положены два закона:

Закон склеивания 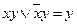(или , где 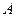- произвольная булева функция, 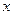- отдельный знак).

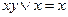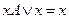Закон поглощения (или , где 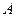- любая булева функция, 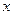- отдельный знак).

Нормальная форма заданной функции (дизъюнктивной и конъюнктивной) называется минимальной, если количество букв, которое она содержит, будет не больше, чем в любой другой ее нормальной форме.

Обратите внимание, что речь идет о минимальном числе букв, а не переменных. Например, 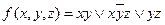содержит 7 букв, но 3 переменных.

Некоторые функции имеют несколько минимальных форм. Они могут быть найдены специальными способами, которым и посвящена данная разработка.

С элементами математической логики можно познакомиться по методической разработке “Элементы теории множеств и математической логики” (Л.С. Тихомирова, И.Н. Иноземцева. Издание ИМИ, 1974 г.).

Введем некоторые необходимые понятия.

Рассмотрим функцию 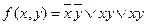. Каждое из слагаемых соответствует только одной единицы в таблице истинности данной функции. Говорят, что каждое слагаемое покрывает единицу функции, а в совокупности они покрывают данную функцию т.е. являются ее покрытием. Но заметим, что упростив функцию 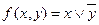, получим более простое покрытие. Оба представления соответствуют одной и той же таблице истинности функции, т.е. обращаются в 1 и 0 на одних и тех же наборах переменных 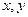. Если обратиться к отдельным слагаемым 2-го представления, нетрудно заметить, что 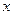обращается в единицу на двух наборах (1, 0), (1, 1), а - на (0, 0), (1, 0), совместно они покрывают единицами все единицы данной функции. Отметим, что оба слагаемых 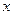и 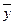обращаются одновременно в нуль на наборе (0, 1), т.е. там, где функция 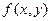равна нулю.

Если функция 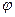равна нулю на тех же наборах переменных, на которых равна нулю данная функция , то говорят, что функция 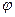входит в функцию.

Другими словами, 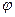входит , если она покрывает нулями все нули функции , т.е. имеет не меньшее количество нулей.

Функция 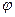, являющаяся элементарным произведением и входящая в функцию , называется импликантой.

Среди импликант данной функции выделяют так называемые простые импликанты, т.е. такие, которые сами входят в , а никакая собственная часть их (элементарное произведение, полученное из данной импликанты исключением из нее одного или нескольких сомножителей) в функцию не входит.

Например: 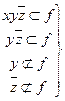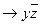- является простой импликантой

(знак 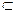означает вхождение в , 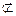означает, что условия вхождения не выполняются).

Простые импликанты представляют собою самые короткие произведения, входящие в данную функцию. Если какое-либо элементарное произведение входит в данную функцию, то при добавлении к нему любых сомножителей новое произведение также будет входить в эту функцию, т.к. оно обращается в нуль вместе с исходным произведением.

Любая булева функция равна дизъюнкции всех своих простых импликант. Это представление функции называется сокращенной дизъюнктивной нормальной формой. Сокращенная форма характеризуется тем, что ее члены самые короткие, из нее уже нельзя исключать ни одной буквы, но можно выбросить некоторые импликанты.

Если из сокращенной формы исключить все возможные члены, то получится тупиковая дизъюнктивная нормальная форма. Тупиковых форм у булевой функции может быть несколько.

Тупиковая форма, содержащая наименьшее число членов, называется кратчайшей дизъюнктивной нормальной формой. Кратчайшая и тупиковые формы в общем случае не совпадают.

Приведем схему упрощения формы булевой функции

Заметим, что минимизацию можно проводить по числу букв, что соответствует минимизации числа входов, любо элементарных логических элементов преобразователя (контактов реле, диодов), либо по числу членов, что соответствует минимизации числа функциональных элементов преобразователя.

Методов минимизации булевых функций существует много. В данном пособии рассматриваются наиболее простые и распространенные.

I метод Геометрический

Применяется он в основном для минимизации функций трех переменных, но его можно обобщить на любое количество переменных. Для трех метод нагляден. Поэтому ограничимся лишь этим случаем.

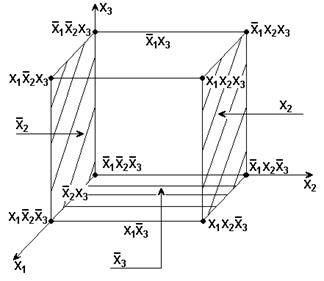Изобразим область определения произвольной булевой функции трех переменных – это вершины трехмерного куба. Элементам куба можно поставить во взаимо-однозначное соответствие конъюнкции различного ранга: вершинам куба – конъюнкции третьего ранга, ребрам – второго, граням – первого. Каждый геометрический эквивалент меньшей размерности покрывается всеми геометрическими эквивалентами большей размерности. Конъюнкции большего ранга покрываются конъюнкциями меньшего ранга (см. рисунок).

Так, например, конъюнкци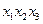и и покрываются конъюнкцией 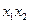(две вершины – ребро);

Конъюнкции 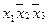, , 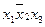, 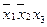покрываются либо двумя конъюнкциями и , либо только 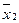(четыре вершины – либо два ребра, либо одна грань).

Булева функция задается множеством своих вершин, т.е. множеством единичных значений. Запись функции в некоторой ДНФ соответствует нахождению покрытия 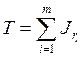, где 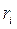- ранги покрыва-ющих интервалов. Задача о нахождении минимальной ДНФ соответствует нахождению такого покрытия 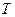, в котором сумма рангов всех покрывающих интервалом является минимальной, т.е. 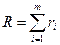- минимально, ибо ранг 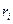совпадает с числом букв, входящий в .

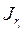Для функци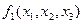й и 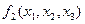на приведенных ниже чертежах мини-мальными формами будут 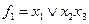, 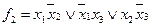или 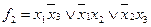Для второй функции задача решается неоднозначно.

Пример: 1 Минимизировать функцию, заданную следующей таблицей истинности

x1
x2
x3
f(x1, x2, x3)

Ее формула в СДНФ имеет вид:

Отметим на чертеже вершины, соответствующие конъюнкциям, входящим в СДНФ данной функции.

Заметим, что четыре вершины лежат в одной грани 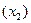, а две на одном ребре 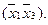Откуда следует, что минимальная форма функции и есть сумма этих интервалов 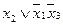, т.е. 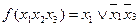Другого варианта решения здесь не может быть. Задача решается однозначно.

2 метод. Метод неопределенных коэффициентов

Этот метод может быть применен для булевых функций от любого числа переменных, однако, для простоты его описания рассмотрим минимизацию функции, зависящей от трех переменных.

Представим функцию в виде следующей ДНФ:

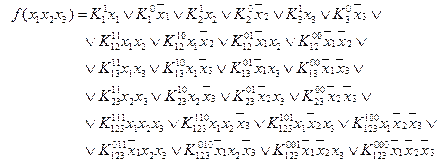
Здесь представлены все возможные конъюнктивные члены, которые могут входить в . Коэффициенты с различными индексами являются неопределенными и подбираются так, чтобы полученная форма была минимальной. Если задать наборы аргументов, подставить в формулу и приравнять полученные выражения (отбрасывая нулевые конъюнкции) значению функции на выбранных наборах, то получим систему уравнений для определения коэффициентов . В общем случае в системе будет 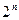уравнений, - число аргументов функции.

(1)

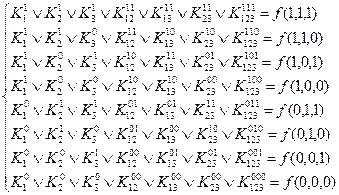
Если функция задана таблицей, то в правой части соответствующих уравнений будут стоять нули и единицы. Для удовлетворения уравнения, в правой части которого стоит нуль, необходимо приравнять нулю все коэффициенты , входящие в это уравнение (это вытекает из определения дизъюнкции).

Рассмотрев все уравнения, в правой части которых стоят нули, и приравняв все коэффициенты этих уравнений нулю, в остальных уравнениях вычеркивают вошедшие в них нулевые коэффициенты. Удобно полученную систему переписать в более сокращенной форме, оставив в ней уравнения, в правой части которых стоят единицы, убрав при этом из этих уравнений нулевые коэффициенты. Затем выбирают в системе самые короткие уравнения. В этих уравнениях приравнивают единице коэффициенты, определяющие конъюнкции наименьшего возможного ранга (это возможно, т.к. дизъюнкция равна единице при обращении в единицу хотя бы одного члена). При этом надо выбрать такие конъюнкции наименьшего ранга, которые чаще встречаются в уравнениях системы. Остальные коэффициенты можно положить равными 0 или 1. Затем рассматривают оставшиеся уравнения и в них выбирают коэффициенты, соответствующие конъюнкциям наименьшего ранга по тому же принципу, и т.д.

Найденные единичные коэффициенты определяют конъюнкции с наименьшим числом знаков, а форма, записанная с этими коэффициентами, определяет минимальную ДНФ данной функции.

Пример 2. Минимизировать функцию (см. пример 1).

Составим систему (обратите внимание на то, что она имеет стандартный вид, лишь в правой части изменяются значения в зависимости от таблицы истинности функции). Для удобства записи системы слева помещают координаты вершин (область определения функции). Верхние индексы коэффициентов комбинируют соответственно из записанных координат вершин с учетом взятых нижних индексов. Например, для второй вершины (0,0,1) верхним индексом для коэффициента 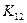будет 00; для - 01 и т.д.

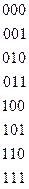
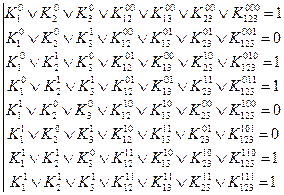
Из уравнений 2, 5, 6 в силу свойств дизъюнкции вытекает, что

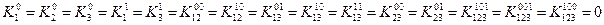
Удобно вычеркнуть уравнения, в правой части которых стоят нули, а в остальных уравнениях вычеркнуть коэффициенты равные нулю.

После этого система примет вид:

(2)

В системе (2) в силу свойства дизъюнкции 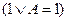можно приравнять единице коэффициент 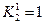, тогда 2, 3, 4 и 5 уравнения этой системы превращаются в тождества, из первого же уравнения системы возьмем 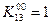. Все остальные коэффициенты во всех уравнениях положим равными нулю.

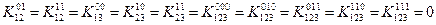
Обратите внимание на тот факт, что единице приравнивают коэффициенты, отвечающие конъюнкциям, содержащим наименьшее число переменных, кроме того, чаще встречающиеся в упрощенной системе уравнений.

Итак, мы нашли , остальные коэффициенты равны нулю. Отсюда минимальная форма данной функции:

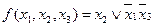
Этот метод является громоздким, практически не используется, но мы рассмотрели его здесь с целью обоснования последующих методов.

метод. Метод минимизирующих карт Карно.

Этот метод по существу представляет собой тот же метод неопределенных коэффициентов, только записанный в более удобной форме.

Рассмотрим следующую таблицу

(3)

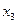
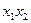
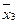
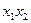
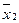
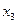
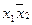
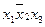
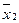
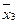
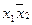
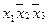
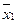
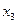
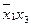
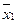
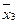
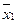
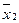
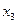
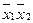
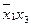
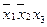
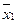
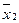
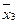
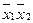
Эта таблица служит более компактной записью системы уравнений (1) метода неопределенных коэффициентов, где вместо коэффициентов в соответствующей клетке записываются сами конъюнкции. Каждая строка таблицы (3) заменяет собою соответственно 1-ое, 2-ое, …… 8-ое уравнения системы (1). Дизъюнкция всех элементов строки таблицы есть значение функции в вершине, определяемой соответствующими переменными. Так, первая строка есть значение функции в вершине , четвертая в 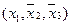или в переводе на координаты соответственно в (1, 1, 1), (1, 0, 0).

Можно показать, что если в СДНФ данной функции не входит какая-либо из восьми конъюнкций последнего столбца, то в минимальную форму этой функции не может входить ни одна из конъюнкций соответствующей строки таблицы.

Пусть, например, в СДНФ не входит конъюнкция , тогда в минимальную форму не входит, например, член (аналогично и другие конъюнкции 3-ей строки).

,

Таким образом, если бы в минимальную форму входил член , то обязательно входил бы член 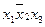, что противоречит предположению.

Таблица (3) и называется минимизирующей картой. Обычно эти карты отпечатаны для соответствующего числа переменных.

Минимизация функции производится по следующим правилам:

1. Все строки таблицы, которые соответствуют конъюнкциям последнего столбца, отсутствующим в СДНФ данной функции, вычеркивают.
2. В столбцах оставшихся строк вычеркивают все элементы, попавшие в вычеркнутые строки.
3. В каждой из невычеркнутых строк выбирают незачеркнутую конъюнкцию, содержащую минимальное число знаков (желательно, чтобы выбранные конъюнкции встречались чаще во всех оставшихся строках).
4. Взяв по одной конъюнкции для всех незачеркнутых строк и записав их дизъюнкцию, получают минимальную форму.

Заметим, что нахождение МДНФ неоднозначно, ибо произволен выбор минимальных конъюнкций в строках. Однако, все получаемые по этому методу МДНФ будут “одинаково минимальны”.

Пример 3. Минимизировать функцию (см. пример 1)

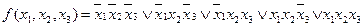
Строим для функции минимизирующую карту

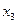
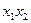
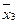
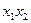
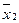
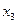
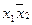
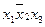
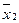
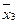
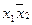
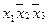
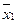
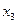
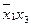
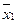
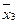
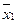
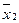
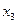
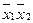
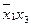
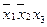
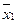
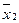
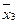
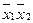
Отметим справа от последнего столбца те конъюнкции, которые входят в СДНФ данной функции. Вычеркнем неотмеченные строки (правило 1), затем вычеркнем в остальных строках (действуя по столбцу) те элементы, которые попали в вычеркнутые строки (правило 2). Во 2-ом столбце (с одной переменной) положим , при этом остальные элементы строк (1, 2, 5, 6 строки), где стоит элемент , положим равными нулю. В строке 8 положим элемент , .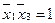

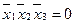Итак, получим МДНФ данной функции в виде:

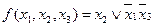
Сравните с результатами, полученными геометрическим методом и методом неопределенных коэффициентов.

Пример 4. Минимизировать функцию.

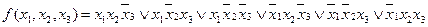
Согласно правилам 1, 2 вычеркиваем конъюнкции

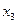
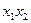
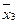
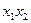
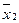
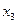
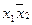
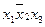
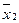
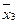
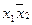
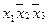
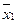
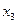
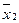
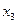
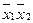
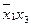
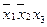
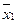
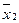
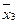
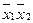
Для удобства табличку оставшихся конъюнкций начертим отдельно, выбросив 1-3 столбцы, 1, 8 строки.

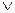
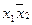
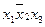
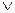
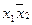
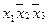
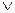
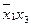
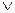
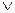
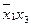
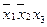
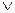
Положим во 2-ой строке 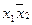равным 1, обведем рамочкой, остальные члены положим равными нулю. Вычеркнем нулевые члены в 6-й строке, в 1-й строке. Выберем из оставшихся строк самые короткие, 1-я и 6-я строки. Положим в них соответственно , остальные члены равными нулю. В строках 4 и 5 будет по одному члену, равному 1. Итак, в каждой строке таблицы есть один член, равный 1, следовательно, минимальная форма функции будет

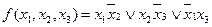
Возможен другой вариант минимальной формы. Рассмотрим на таблице.

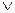
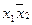
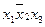
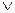
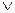
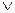
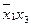
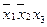
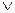
Пусть в 4-й строке 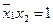, а остальные члены равны нулю. Тогда в строке 5: 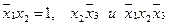можно положить равными нулю. Вычеркнем 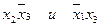в 1-й и 6-й строках (они короче других), положим соответственно 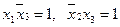. Тогда в строках 2 и 3 будет по одному члену, равному единице. Итак, минимальная форма функции

Методы неопределенных коэффициентов и минимизирующих карт приводят к громоздким записям (число строк таблицы для функции переменных равно 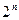, а число столбцов ). Использование этих методов уже для порядка 8-10 становится затруднительным.