 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Гражданская оборона Украины. Задания,организационное строение и порядок функционирования 1 страница
|
|
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
КУРС ЛЕКЦИЙ
МОСКВА 2010
ВВЕДЕНИЕ
При исследовании реальной системы (объекта) обычно систему представляют в виде математической модели, что позволяет использовать для ее исследования различные математические методы. Для исследования системы по е математической модели необходимо найти вычислительный метод, приводящий к решению поставленной задачи. Рассмотрению совокупности вычислительных методов и посвящена дисциплина «Вычислительная математика».
Вычислительная математика играет важную роль в естественно-научных, инженерно-технических и экономических исследованиях.
Реально на практике мы работаем с дискретностью: конечным множеством экспериментально полученных данных, дискретным описанием непрерывных процессов, что широко используется для решения многих прикладных задач. Это дает возможность разрабатывать эффективные машинные алгоритмы решения задач. Владение основными понятиями и теоретическими результатами дисциплины «Вычислительная математика» является необходимым условием подготовки квалифицированного инженера.
Ниже рассматриваются основные математические методы, применяемые в инженерной практике при создании и исследовании систем (объектов).
Материал приводится в виде курса лекций, включающего в себя девять разделов. Для некоторых из разделов студент выполняет свой вариант контрольного задания на самостоятельную работу. Индивидуальное задание студента находится по последней паре цифр номера зачетной книжки. Строка выбирается по предпоследней цифре зачетной книжки, а столбец таблицы выбирается по последней цифре номера зачетной книжки. Например, зачетная книжка № 432074. Задание находится в строке 7 и столбце 4 таблицы задания на самостоятельную работу.
Цель дисциплины – дать студентам необходимые знания для работы с формальным математическим аппаратом, обучить стандартным методам и приемам приближенного решения прикладных задач.
При изучении дисциплины используются знания, навыки и умения, приобретенные студентами в процессе изучения общего курса высшей математики.
В результате изучения дисциплины «Математика: вычислительная математика» студенты должны:
- ЗНАТЬ теоретические основы и методы, используемые для приближенного решения прикладных задач.
- УМЕТЬ использовать полученные знания при построении и описании моделей реальных процессов, при разработке методов и алгоритмов решения прикладных задач.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ, ИХ СОЗДАНИЕ
И СОВЕРШЕНСТВОВАНИЕ
1.1 ЭТАПЫ РЕШЕНИЯ ЗАДАЧИ НА КОМПЬЮТЕРЕ.
При решении задачи на компьютере основная роль все-таки принадлежит человеку. Машина лишь выполняет его задания по разработанной программе. Широкое внедрение математики во все сферы жизни вызвано необходимостью анализа и прогнозирования явлений и процессов. Для осуществления указанных целей, прежде всего необходимо разработать математическую модель рассматриваемого явления. Математическая модель – то описание наиболее существенных свойств и особенностей явления на языке математических понятий и уравнений.
Схема исследования технической задачи представлена на рисунке:
|
Построение модели задачи начинается выделения его наиболее существенных черт и свойств и описания их с помощью математических соотношений. Математическая модель, основанная на упрощении, идеализации, не тождественна реальному явлению, а является его приближенным описанием. Однако благодаря замене реального объекта приближенной моделью становится возможным его математическое описание. Математика позволяет провести детальный анализ рассматриваемого явления, предсказать его поведение в различных условиях и в будущем.
Как правило, приходится использовать наряду с точными методами и приближенные методы, обеспечивающие получение результата с заданной точностью. Поэтому важной задачей по выбору вычислительного метода является оценка погрешности решения. Процесс решения задачи согласно выбранному методу описывается в виде алгоритма. После анализа результатов разработчик сопоставляет их с поставленной задачей и, если необходимо, меняет модель, метод, алгоритм и программу. Цикл, показанный на рисунке, повторяется до тех пор, пока цель не будет достигнута.
Основным критерием истины является эксперимент. Только практика позволяет сравнить различные гипотетические модели и выбрать из них наиболее простую и достоверную, указать области применимости различных моделей и направление их совершенствования.
1.2 ПРИМЕРЫ ИСПОЛЬЗУЕМЫХ ПОДХОДОВ
И РЕШАЕМЫХ ЗАДАЧ.
Рассмотрим развитие модели на примере известной задачи баллистики об определении траектории тела, выпущенного с начальной скоростью V0 под углом x0 к горизонту.
Для начала предположим, что скорость V0 и дальность полета тела небольшие. Тогда для данной задачи будет справедлива математическая модель Галилея, основанная на следующих допущениях:
1) Земля – инерциальная система;
2) ускорение свободного падения g = const
3) сопротивление воздуха отсутствует.
В этом случае составляющие скорости V движения тела по осям X и Y равны (см. график к траектории полета тела).
Vx=V0cosα0, Vy=V0sinα0 – gt, а их пути являются функциями времени.
| Vy |
| Vx |
| модель Галилея |
| α0 |
| У |
| X |
| реальная траектория |
| Рис. Траектория полета тела |
X= V0tcosα0; Y= V0tsinα0 –  , где t – время движения.
, где t – время движения.
Определяя t из первого уравнения t=  и подставляя его во второе, получаем уравнение траектории тела, представляющего собой параболу
и подставляя его во второе, получаем уравнение траектории тела, представляющего собой параболу
| 2V02cos2α0 |
| y = xtgα0 – |
| x2g |
Из условия y=0 получаем дальность полета тела
| l = |
| g |
| sin2α0 (1) |
| V02 |
Однако, как показывает практика, результаты, получаемые на основе этой модели, оказываются справедливыми лишь при малых скоростях движения тела. С увеличением скорости V0 дальность полета становится меньше величины, даваемой формулой (1). Такое расхождение эксперимента с расчетной формулой (1) говорит о неточности модели Галилея, не учитывающей сопротивление.
Дальнейшее уточнение модели баллистической задачи было сделано Ньютоном. Это позволило с достаточной точностью рассчитать траектории движения пушечных ядер, выстреливаемых со значительными начальными скоростями.
Переход от гладкоствольного к нарезному оружию позволил увеличить скорость, дальность и высоту полета снарядов, что вызвало дальнейшее уточнение математической модели задачи. В новой математической модели были пересмотрены все допущения, принятые в модели Галилея. Земля уже не считалась плоской и инерциальной системой, а сила земного притяжения не принималась постоянной.
Последующее совершенствование математической модели задачи связано с использованием методов теории вероятности.
В результате последовательных уточнений была создана математическая модель, наиболее точно описывающая задачу внешней баллистики. Совпадение ее данных с результатами стрельб показало хорошее совпадение.
Хорошим и наглядным примером является разработка и внедрение математической модели полета самолета для различных целей.
На этих примерах показаны этапы создания, развития и уточнения математической модели объекта, которые сопоставляются постоянно сопоставлением и проверкой практикой. Именно недостаточно хорошее совпадение результатов, предоставляемых моделью, с объектом вызывает дальнейшее совершенствование модели.
Наконец отметим, что выбор конкретной математической модели для ее анализа необходимо производить из условия обеспечения достаточной точности и простоты модели. При этом всегда следует помнить, что нельзя стрелять из пушки по воробьям, т.е. не следует использовать очень точную и сложную модель, когда требуется небольшая точность результатов.
2. ПОГРЕШНОСТИ РЕЗУЛЬТАТОВ
ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧ
2.1 ИСТОЧНИКИ И КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ.
Анализ погрешности результатов вычислений должен являться непременной частью при математическом моделировании объекта.
Причины возникновения погрешностей:
1. математическая модель объекта не является точной ее копией (неточно задаются исходные данные).
2. Применяемый математический метод дает приближенное решение задачи.
3. При вводе данных в ЭВМ и выполнении математических операций производится округление чисел.
В результате получаются соответствующие погрешности:
неустранимая погрешность
погрешность метода
вычислительная погрешность.
Пример: математическая модель движения маятника представляется уравнением:
| lφ"(t)+μφ'(t)+gsinφ(t)=0 |
φ(t) – угол отклонения маятника;
l – длина маятника;
μ – коэффициент трения;
t – время.
В данной модели уже заложена неустранимая погрешность, поскольку она соответствует объекту лишь приближенно.
Данное дифференциальное уравнение не решается в явном виде. При применении математического метода возникает погрешность метода, а при выполнении арифметических операций – вычислительная погрешность.
| ~ |
| ~ |
| ~ |
In* – приближенное значение параметра, получаемое при вычислениях.
| ~ |
| ~ |
| ~ |
ρ3=|I – In*| – вычислительная погрешность.
| ~ |
2.2 АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ
ПОГРЕШНОСТЬ. ЗНАЧАЩАЯ ЦИФРА. ЧИСЛО
ВЕРНЫХ ЗНАКОВ.
Пусть А – точное значение параметра;
а – приближенное его значение.
Тогда абсолютной погрешностью приближения a называют величину
|A – a| ≤ ∆(a)
Отсюда следует, что точное число А заключено в границах
a–∆(a) ≤ A ≤ a+∆(a)
Следовательно, a–∆(a) есть приближенное число А по недостатку, а a+∆(a) – приближенное число А по избытку. Для краткости пользуются записью
A = a±∆(a)
Пример 1. Определить абсолютную погрешность числа а=3,14, заменяющего число π.
Решение: т.к.
3,14<π <3,15, то |π – a|<0,01
Следовательно, ∆(a)=0,01
Абсолютная погрешность не достаточна для характеристики точности числа. Так, например, если при измерении длин двух стержней получено
l1=100,8±0,1 см и l2=5,2±0,1 см
то качество первого измерения выше, чем второго.
Точность данных измерений оценивается абсолютной погрешностью, приходящейся на единицу длины, называемой относительной погрешностью, т.е. относительной погрешностью называют величину
δ(a) =  =
= 
Если ∆a<<a, то δ(a)=  и обычно вычисляется в процентах.
и обычно вычисляется в процентах.
Известно, что всякое число а может быть представлено в виде, например:
141,59…=1∙102+4∙101+1∙100+5∙10-1+9∙10-2+…
Введем понятие значащей и верной цифр.
Значащими цифрами числа а называются все цифры с первой ненулевой слева.
Например:
а=0,00 5860
Все подчеркнутые цифры являются значащими.
Значащую цифру называют верной, если абсолютная погрешность этого числа меньше или равна половине единицы разряда, соответствующего этой цифре.
Например: для числа 2,15 абсолютная погрешность не превосходит 0,005, если абсолютная погрешность меньше 0,005, то следует писать 2,150 – это и есть верные значащие цифры.
Часто возникает необходимость в округлении чисел. Чтобы округлить число до n значащих цифр, отбрасывают все цифры, стоящие справа от n-ой значащей цифры. При этом:
1) если первая из отброшенных цифр меньше 5, то оставшиеся знаки остаются без изменения;
2) если первая из отброшенных цифр больше 5, то к последней оставшейся цифре прибавляется единица;
3) если первая из отброшенных цифр равна 5 и среди остальных отброшенных цифр имеются ненулевые, то последняя оставшаяся цифра увеличивается на единицу;
4)если же первая из отброшенных цифр равна 5 и все остальные отброшенные цифры являются нулями, то последняя оставшаяся цифра сохраняется неизменной, если она четная и увеличивается на единицу, если она нечетная (правило четной цифры).
Пример 1. Округляя число π=3,14159… до пяти, четырех и трех значащих цифр, получим приближенные числа 3,1416; 3,142; 3,14 с абсолютными погрешностями, меньшими 0,5∙10-4; 0,5∙10-3; 0,5∙10-2.
Пример 2. Округляя число 1,2500 до двух значащих цифр, получим приближенное число 1,2 с абсолютной погрешностью, равной 0,5∙10-1=0,05.
СВЯЗЬ ЧИСЛА ВЕРНЫХ ЗНАКОВ С ОТНОСИТЕЛЬНОЙ
ПОГРЕШНОСТЬЮ.
ТЕОРЕМА. Если положительное приближенное число имеет n верных знаков, то относительная погрешность его δ(а) не превосходит величину
δ(а)≤0,1n-1/2am,
где am – первая значащая цифра числа а.
Пример: определить относительную погрешность числа а, если вместо числа π взять а=3,14.
В нашем случае am=3, n=3 отсюда δ(а) ≤  =
=  = 0,1666%
= 0,1666%
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
ЗАДАНИЕ 1
ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ
1. Определить, какое равенство точнее.
2. Округлить сомнительные цифры числа, оставив верные знаки.
3. Найти абсолютные и относительные погрешности, если они имеют только верные числа.
Задания приведены в таблице 1.
ТАБЛИЦА 1
| 0,1,2 | 3,4,5,6 | 7,8,9 | |
1) 6/7=0,857;
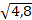 =2,19;
2)5,435±0,0028;
3)8,345. =2,19;
2)5,435±0,0028;
3)8,345.
| 1)2/21=0,095;
 =4,69;
2)2,4543±0,0032;
3)0,347. =4,69;
2)2,4543±0,0032;
3)0,347.
| 1)4/17=0.235;
 =3,24;
2)0,5748±0,0034;
3)0,5748. =3,24;
2)0,5748±0,0034;
3)0,5748.
| |
1)15/7=2,14;
 =3,16;
2)2,3485±0,0042;
3)2,3445. =3,16;
2)2,3485±0,0042;
3)2,3445.
| 1)12/11=1,091;
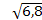 =2,61;
2)0,12356±0,00036;
3)12,45. =2,61;
2)0,12356±0,00036;
3)12,45.
| 1)6/11=0,545;
 =9,11;
2)2,3485±0,0042;
3)41,72. =9,11;
2)2,3485±0,0042;
3)41,72.
| |
1)13/17=0,765;
 =5,56;
2)3,6878±0,0068;
3)14,862. =5,56;
2)3,6878±0,0068;
3)14,862.
| 1)7/22=0,318;
 =3,60;
2)27,1548±0,0016;
3)0,3648. =3,60;
2)27,1548±0,0016;
3)0,3648.
| 1)17/11=1,545;
 =4,243;
2)0,8647±0,0013;
3)2,4516. =4,243;
2)0,8647±0,0013;
3)2,4516.
| |
1)5/3=1,667;
 =6,16;
2)13,537±0,0026;
3)62,74. =6,16;
2)13,537±0,0026;
3)62,74.
| 1)51/11=4,64;
 =5,91;
2)38,4258±0,0014;
3)6,743. =5,91;
2)38,4258±0,0014;
3)6,743.
| 1)6/7=0,857;
 =6,40;
2)32,7488±0,0012;
3)3,425. =6,40;
2)32,7488±0,0012;
3)3,425.
| |
1)17/19=0,895;
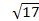 =4,12;
2)3,6878±0,0013;
3)0,3825. =4,12;
2)3,6878±0,0013;
3)0,3825.
| 1)16/7=2,28;
 =3,32;
2)5,6483±0,0017;
3)16,383. =3,32;
2)5,6483±0,0017;
3)16,383.
| 1)7/3=2,33;
 =7,61;
2)0,39642±0,00022;
3)26,3. =7,61;
2)0,39642±0,00022;
3)26,3.
|
ПРИМЕРЫ
Заданы:
1) а1 = 9/11 = 0,818 и а2 =  = 4,24;
= 4,24;
2) 72,353±0,026;
3) 0,4357.
РЕШЕНИЕ:
1. Находим с большим числом десятичных знаков а1=9/11=0,81818…, а2=  =4,2426…
=4,2426…
Вычислим абсолютные погрешности, округляя их с избытком:
∆a1 = | 0,81818–0,818 | ≤ 0,00019
∆a2 = | 04,2426–4,24 | ≤ 0,0027
Предельные относительные погрешности составляют:
δ1 = ∆a1/а1 = 0,00019/0,818 = 0,00024 = 0,024%
δ2 = ∆a2/а2 = 0,0027/4,24 = 0,00064 = 0,064%
Т.к. δ1<δ2, то равенство 9/11 = 0,818 является более точным.
2. Здесь а = 72,353±0,026. По условию погрешность ∆a = 0,026 < 0,05. Это значит, что в числе 72,353 верными являются цифры 7, 2, 3. По правилам округления найдем приближенное значение числа, сохранив десятичные доли:
а1 = 72,4; ∆a1 = ∆a+∆окр = 0,026 + 0,047 = 0,073
Полученная погрешность меньше 0,5. Поэтому надо уменьшить число цифр в приближенном числе до двух.
а2 = 72; ∆a1 = ∆a+∆окр = 0,026 + 0,353 = 0,379
Так как ∆a2<0,5, то обе оставшиеся цифры верны.
3. Так как все четыре цифры а=0,4357 верны, то абсолютная погрешность ∆а=0,00005, а относительная погрешность
δа =  =
=  ∙ 100 = 0,01147
∙ 100 = 0,01147
2.3 ДЕЙСТВИЯ НАД ПРИБЛИЖЕННЫМИ
ЧИСЛАМИ.
При сложении и вычитании их абсолютные погрешности складываются.
При умножении и делении их относительные погрешности складываются.
Относительная погрешность степени или корня от приближенного числа равна относительной погрешности числа, умноженной на степень или деленной на показатель корня соответственно.
Для случая двух приближенных чисел а и b эти правила можно выразить математически:
∆(a±b)= ∆a±∆b;
| (2.1) |
δ(a/b)= δa+δb;
δ(ak)=k∙δa;
δ( )=
)=  .
.
Во избежание завышения абсолютной погрешности суммы(разности) большого количества слагаемых, округленных до m-ого десятичного знака (т.е. их погрешности оцениваются величиной 0,5∙10-m), абсолютная погрешность суммы (разности) оценивается правилом Чеботарева:
∆s =  ∙ 0,5 ∙ 10-m
∙ 0,5 ∙ 10-m
n – число слагаемых.
Если среди слагаемых имеется одно число, абсолютная погрешность которого значительно превосходит погрешности остальных слагаемых, то абсолютная погрешность суммы (разности) считается равной этой наибольшей погрешности.
Пример 2.1
Найти сумму приближенные чисел 0,348; 0,1834; 345,4; 235,2; 11,75; 9,27.
Решение: наибольшую абсолютную погрешность ∆=0,05 имеют два числа 345,4 и 235,2. Поэтому можно считать, что абсолютная погрешность суммы составляет 2∆=0,10. Так как количество слагаемых невелико, то округляем слагаемые до 0,01
| 345,4 235,2 11,75 9,27 0,35 0,18 | В окончательном результате последний знак отбрасывается: S=602,15 При этом к ранее определенной погрешности ∆s=0,10 добавляем погрешность округления 0,05, что дает ∆s=0,15, а округляя это число, получим ∆s=0,2 |
| S=602,15 |
Т.о. полный учет всех погрешностей только усложнил бы расчет, не внося существенных уточнений в результат.
2.4 ПОГРЕШНОСТИ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ФУНКЦИИ.
Пример 2.2. Найти относительную погрешность функции

Используя формулы (2.1)
δy =  [ δ(a+b) + 3δx + δ(1-x) ] =
[ δ(a+b) + 3δx + δ(1-x) ] = 

Полученная оценка относительной погрешности содержит в знаменателе  . Ясно, что при x≈1 можно получить завышенную погрешность. Поэтому при организации вычислительных алгоритмов следует избегать вычитания близких чисел, при возможности алгоритм надо видоизменить во избежание потери точности на некотором этапе вычисления.
. Ясно, что при x≈1 можно получить завышенную погрешность. Поэтому при организации вычислительных алгоритмов следует избегать вычитания близких чисел, при возможности алгоритм надо видоизменить во избежание потери точности на некотором этапе вычисления.
Рассмотрим функцию одной переменной y=f(x). Пусть a – приближенное значение аргумента х. ∆а – его абсолютная погрешность. Абсолютную погрешность функции можно считать ее приращением, которое возникает при изменении аргумента на ∆а. это приращение можно заменить дифференциалом: ∆y≈dy. Тогда для оценки абсолютной погрешности получим выражение:
∆y=| f '(x) |∆a
Для функции нескольких аргументов. Например, оценка абсолютной погрешности функции U=f(x,y,z), приближенные значения аргументов, которой соответственно a,b,c имеет вид:

Здесь ∆a, ∆b, ∆c – абсолютные погрешности аргументов.
Относительная погрешность находится по формуле:
δU = 
ПРИМЕР 2.3
Найти абсолютную и относительную погрешность объема шара.
| Дано: d=3,7±0,05 см π=3,14+0,0016 | Решение:
V =  ; ;  = =  = 8,44 = 8,44
 = =  = 21,5
∆V= = 21,5
∆V=  Поэтому V=26,5±1,1см3
ΔV=
Поэтому V=26,5±1,1см3
ΔV= 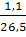 = 0,041 ≈ 4% = 0,041 ≈ 4%
|
| Найти: ∆V=?, δv=? | |
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
Определить абсолютную и относительную погрешности объема параллелепипеда, имеющего стороны:
a=5±0,05см
b=7±0,05см
с=4±0,02см
Решение:
V=a*b*c=140см2


3. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ
УРАВНЕНИЙ.
Система n уравнений от n неизвестных называется линейной, если неизвестные входят в неё только в первой, например:
| (2.1) |
a21x1 + a22x2 + … + a2nxn = b2
……………………………………
an1x1 + an2x2 + … + annxn = bn
Здесь aij-коэффициенты уравнений;
xi- неизвестные;
bi- свободные члены уравнений (i,j=1,2..n).
Записывая коэффициенты этой системы aij в виде прямоугольной таблицы, а неизвестные xi и свободные члены bi в виде столбцов.
A=  , x=
, x=  , b =
, b = 
Систему уравнений (2.1) можно записать в векторно-матричном виде:
Ax=b
Здесь: A-матрица коэффициентов системы
x- вектор-столбец неизвестных
b- вектор-столбец свободных членов.
Так как алгебра матриц широко используется в теории линейных уравнений, рассмотрим ее основные понятия.
3.1 ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ МАТРИЦ.
Матрицей называется система m×n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов
A= 
Если m=n, то матрицу называют квадратной порядка n. Прямоугольную матрицу типа m×n обозначают в виде A=[aij]m×n.
Квадратная матрица вида
A= 
называется диагональной и обозначается A=[a1,a2,…,an].
Если ai=1(i=1,2…,n), то матрица называется единичной и обозначается буквой E
E= 
Матрица называется нулевой, если все ее элементы равны нулю. Она обозначается Omn. Матрица называется верхней треугольной, если все элементы ее ниже главной диагонали равны нулю, и нижней треугольной, если ее элементы выше главной диагонали нулевые.
Дата публикования: 2014-11-18; Прочитано: 263 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
