 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Краткие теоретические сведения. 2 страница
|
|
Тема 4. Системы векторов. N-мерное векторное пространство. Евклидово пространство.
Арифметическим вектором называют упорядоченную совокупность из 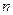 чисел:
чисел: 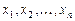 и обозначают
и обозначают 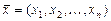 . Числа
. Числа 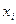 называют компонентами вектора
называют компонентами вектора 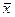 , число компонент называют его размерностью.
, число компонент называют его размерностью.
Векторы 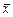 и
и 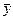 называют равными, если они одинаковой размерности и их соответствующие компоненты равны:
называют равными, если они одинаковой размерности и их соответствующие компоненты равны: 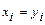 ,
, 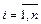 .
.
Суммой векторов 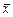 и
и 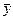 одной размерности, называют вектор
одной размерности, называют вектор 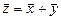 той же размерности, для которого:
той же размерности, для которого: 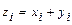 ,
, 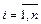 .
.
Произведением вектора 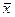 на число
на число 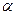 называют вектор
называют вектор 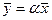 той же размерности, для которого:
той же размерности, для которого: 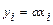 ,
, 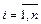 .
.
Линейной комбинациейвекторов 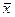 и
и 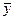 одной размерности, называют вектор
одной размерности, называют вектор 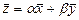 той же размерности (
той же размерности (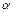 и
и 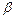 - произвольные числа), для которого:
- произвольные числа), для которого: 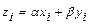 ,
, 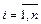 .
.
Множество всех 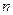 -мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называют векторнымпространством и обозначают
-мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называют векторнымпространством и обозначают 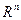 .
.
Систему векторов 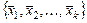 называют линейно зависимой, если найдутся числа
называют линейно зависимой, если найдутся числа 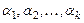 ,
, 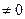 одновременно, такие, что
одновременно, такие, что 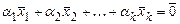 (где
(где 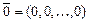 - нулевой вектор), в противном случае, систему называют линейно независимой.
- нулевой вектор), в противном случае, систему называют линейно независимой.
Базисом системы векторов 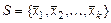 называют упорядоченную систему векторов
называют упорядоченную систему векторов 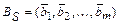 , удовлетворяющую условиям:
, удовлетворяющую условиям:
1) 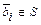 ,
, 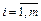 ; 2) система
; 2) система 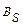 линейно независима; 3) для любого вектора
линейно независима; 3) для любого вектора 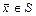 найдутся числа
найдутся числа 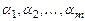 такие, что
такие, что 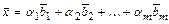 . Коэффициенты
. Коэффициенты 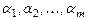 , однозначно определяемые вектором
, однозначно определяемые вектором 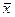 , называют координатами вектора в базисе
, называют координатами вектора в базисе 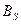 , а формулу называют разложениемвектора
, а формулу называют разложениемвектора 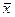 по базису
по базису 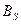 и пишут:
и пишут: 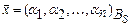 .
.
В пространстве 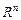 базисом является каждая упорядоченная система из
базисом является каждая упорядоченная система из 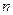 линейно независимых векторов:
линейно независимых векторов: 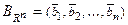 . Формулу
. Формулу 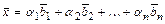 называют разложениемвектора
называют разложениемвектора 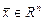 по базису
по базису 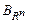 , коэффициенты
, коэффициенты 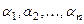 - координатами вектора в базисе
- координатами вектора в базисе 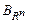 и пишут
и пишут 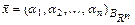 .
.
Всякая упорядоченная система из 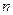 векторов
векторов 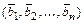 образует базис
образует базис 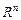 , если определитель, столбцами которого являются компоненты векторов
, если определитель, столбцами которого являются компоненты векторов 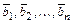 , не равен нулю.
, не равен нулю.
Пространство 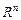 , в котором введено скалярное произведение векторов, удовлетворяющее определённым требованиям (аксиомам), называют евклидовым. Скалярным произведением двух векторов
, в котором введено скалярное произведение векторов, удовлетворяющее определённым требованиям (аксиомам), называют евклидовым. Скалярным произведением двух векторов 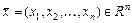 и
и 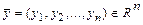 называют число:
называют число: 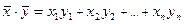 .
.
Тема 5. Линейные операторы. Собственные числа и векторы.
Оператором называется закон (правило), по которому каждому вектору 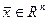 ставится в соответствие единственный вектор
ставится в соответствие единственный вектор 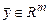 , и пишут
, и пишут 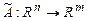 или
или 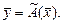 В дальнейшем, рассматривается случай
В дальнейшем, рассматривается случай 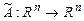 (преобразование пространства
(преобразование пространства 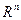 ). Оператор
). Оператор 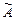 называется линейным, если для любых векторов
называется линейным, если для любых векторов 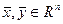 и действительных чисел
и действительных чисел 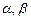 выполнено условие:
выполнено условие: 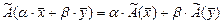 .
.
Если 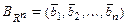 - базис пространства
- базис пространства 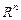 , то матрицей линейного оператора
, то матрицей линейного оператора 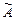 в базисе
в базисе 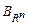 называется квадратная матрица
называется квадратная матрица 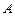 порядка
порядка 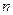 , столбцами которой являются столбцы координат векторов
, столбцами которой являются столбцы координат векторов 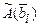 . Между линейными операторами, действующими в
. Между линейными операторами, действующими в 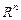 и квадратными матрицами порядка
и квадратными матрицами порядка 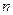 , существует взаимно однозначное соответствие, что позволяет оператор
, существует взаимно однозначное соответствие, что позволяет оператор 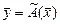 представить в матричном виде
представить в матричном виде 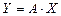 , где
, где 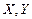 - матрицы-столбцы координат векторов
- матрицы-столбцы координат векторов 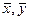 ,
, 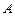 - матрица оператора
- матрица оператора 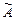 в базисе
в базисе 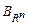 .
.
Для линейных операторов, действующих в 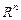 вводятся следующие операции: 1) сложение операторов:
вводятся следующие операции: 1) сложение операторов: 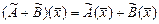 ; 2 ) умножение операторов на число:
; 2 ) умножение операторов на число: 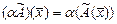 ; 3) умножение операторов:
; 3) умножение операторов: 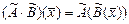 .
.
Обратным к оператору 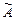 называется оператор
называется оператор 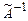 такой, что
такой, что 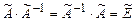 , где
, где 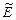 - единичный (тождественный) оператор, реализующий отображение
- единичный (тождественный) оператор, реализующий отображение 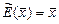 . Обратный оператор
. Обратный оператор 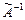 существует только для невырожденных операторов
существует только для невырожденных операторов 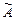 (операторов, матрица которых является невырожденной). Все, рассмотренные выше, действия над линейными операторами выполняют, выполняя аналогичные действия над их матрицами.
(операторов, матрица которых является невырожденной). Все, рассмотренные выше, действия над линейными операторами выполняют, выполняя аналогичные действия над их матрицами.
Пусть число 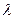 и вектор
и вектор 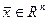 ,
, 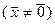 , таковы, что выполняются равенства:
, таковы, что выполняются равенства: 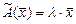 или
или 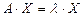 . Тогда число
. Тогда число 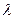 называется собственным числом линейного оператора
называется собственным числом линейного оператора 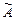 (или матрицы
(или матрицы 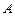 ), а вектор
), а вектор 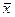 - собственным вектором этого оператора (или матрицы), соответствующим собственному числу
- собственным вектором этого оператора (или матрицы), соответствующим собственному числу 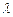 . Равенство
. Равенство 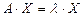 может быть записано в виде
может быть записано в виде 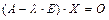 , где
, где 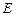 - единичная матрица порядка
- единичная матрица порядка 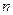 ,
, 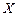 - матрица-столбец координат собственного вектора
- матрица-столбец координат собственного вектора 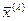 , соответствующего собственному числу
, соответствующего собственному числу 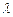 ,
, 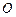 - нулевая матрица-столбец.
- нулевая матрица-столбец.
Характеристическим уравнением оператора 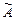 (или матрицы
(или матрицы 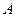 ) называется уравнение:
) называется уравнение: 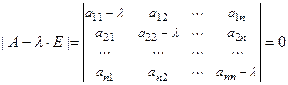 .
.
Множество собственных чисел оператора (или матрицы) совпадает с множеством корней его характеристического уравнения: 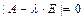 , а множество собственных векторов, отвечающих собственному числу
, а множество собственных векторов, отвечающих собственному числу 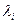 , совпадает с множеством ненулевых решений матричного уравнения:
, совпадает с множеством ненулевых решений матричного уравнения: 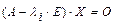 .
.
Тема 6. Квадратичные формы.
Квадратичной формой 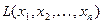 (или кратко
(или кратко 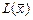 ) от
) от 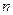 -переменных называется однородный многочлен второй степени с действительными коэффициентами:
-переменных называется однородный многочлен второй степени с действительными коэффициентами: 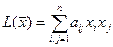 , где
, где 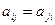 . Квадратичную форму всегда можно записать в матричном виде:
. Квадратичную форму всегда можно записать в матричном виде: 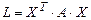 , где
, где 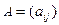 - матрица квадратичной формы (являющаяся симметрической, так как выполняется условие
- матрица квадратичной формы (являющаяся симметрической, так как выполняется условие 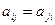 ),
), 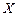 - матрица-столбец,
- матрица-столбец, 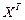 - матрица-строка, составленные из переменных
- матрица-строка, составленные из переменных 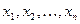 .
.
Квадратичная форма называется невырожденной, если её матрица является невырожденной.
Квадратичная форма называется канонической, если она имеет вид:
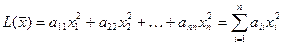 .
.
Всякую квадратичную форму всегда можно привести к каноническому виду, например, методами Лагранжа и ортогональных преобразований.
Квадратичные формы подразделяют на различные типы в зависимости от множества их значений. Квадратичная форма 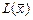 называется:
называется:
положительно (отрицательно) определённой, если для любого 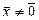 выполняется неравенство
выполняется неравенство 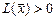 (
(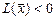 ); неотрицательно (неположительно) определённой, если для любого
); неотрицательно (неположительно) определённой, если для любого 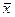 выполняется неравенство
выполняется неравенство 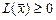 (
(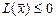 ), причём существует
), причём существует 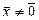 , для которого
, для которого 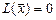 ; знакопеременной (или неопределённой), если существуют такие
; знакопеременной (или неопределённой), если существуют такие 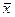 и
и 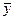 , что
, что 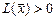 и
и 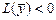 .
.
Невырожденная квадратичная форма может быть либо положительно определённой, либо отрицательно определённой, либо знакопеременной. Тип невырожденной квадратичной формы можно определить, проверяя знаки главных миноров матрицы квадратичной формы.
Пусть 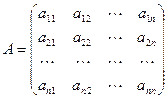 , где
, где 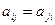 - матрица квадратичной формы. Главными минорами матрицы
- матрица квадратичной формы. Главными минорами матрицы 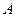 называются миноры порядка
называются миноры порядка 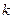
(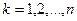 ), составленные из первых
), составленные из первых 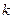 строк и первых
строк и первых 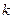 столбцов матрицы:
столбцов матрицы: 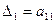 ,
, 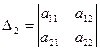 ,
, 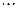 ,
, 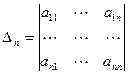 .
.
Критерием знакоопределённости невырожденной квадратичной формы является критерий Сильвестра:
- квадратичная форма 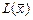 положительно определена тогда и только тогда, когда все главные миноры её матрицы положительны, т.е.
положительно определена тогда и только тогда, когда все главные миноры её матрицы положительны, т.е. 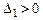 ,
, 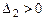 ,
, 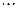 ,
, 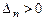 ;
;
- квадратичная форма 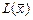 отрицательно определена тогда и только тогда, когда для всех главных миноров её матрицы выполняются неравенства:
отрицательно определена тогда и только тогда, когда для всех главных миноров её матрицы выполняются неравенства: 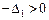 ,
, 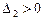 ,
, 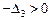 ,
, 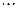 ,
, 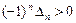 (все миноры нечётного порядка отрицательны, а чётного – положительны);
(все миноры нечётного порядка отрицательны, а чётного – положительны);
- квадратичная форма 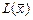 знакопеременна тогда и только тогда, когда для главных миноров её матрицы выполняется хотя бы одно из условий: один из главных миноров равен нулю, один из главных миноров чётного порядка отрицателен, два главных минора нечётного порядка имеют разные знаки.
знакопеременна тогда и только тогда, когда для главных миноров её матрицы выполняется хотя бы одно из условий: один из главных миноров равен нулю, один из главных миноров чётного порядка отрицателен, два главных минора нечётного порядка имеют разные знаки.
Тема 7. Векторная алгебра.
Вектором (геометрическим) называется направленный отрезок, задаваемый упорядоченной парой точек (началом и концом вектора). Обозначают вектор 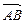 или
или 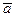 . Расстояние между началом и концом вектора называется его длиной и обозначается
. Расстояние между началом и концом вектора называется его длиной и обозначается 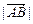 или
или 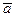 . Углом между векторами
. Углом между векторами 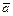 и
и 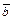 называется угол
называется угол 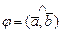 ,
, 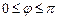 , на который следует повернуть один из векторов, чтобы его направление совпало с направлением другого вектора, при условии, что их начала совпадают. Проекцией вектора
, на который следует повернуть один из векторов, чтобы его направление совпало с направлением другого вектора, при условии, что их начала совпадают. Проекцией вектора 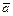 на вектор
на вектор 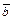 называется число
называется число 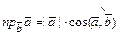 .
.
Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называются компланарными, если они расположены в одной плоскости или в параллельных плоскостях.
Векторы 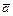 и
и 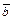 называются равными и пишут
называются равными и пишут 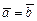 , если они коллинеарны, одинаково направлены и имеют равные длины. Векторы
, если они коллинеарны, одинаково направлены и имеют равные длины. Векторы 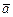 и
и 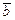 называются противоположными и пишут
называются противоположными и пишут 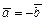 , если они коллинеарны, направлены в разные стороны и имеют равные длины.
, если они коллинеарны, направлены в разные стороны и имеют равные длины.
Суммой векторов 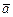 и
и 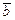 называется вектор
называется вектор 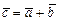 , соединяющий начало вектора
, соединяющий начало вектора 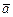 и конец вектора
и конец вектора 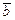 , при условии, что конец вектора
, при условии, что конец вектора 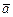 совпадает с началом вектора
совпадает с началом вектора 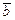 (правило треугольника). Произведением вектора
(правило треугольника). Произведением вектора 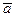 на действительное число
на действительное число 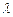 называется вектор
называется вектор 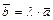 :
:
1) коллинеарный вектору 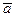 ; 2) имеющий длину
; 2) имеющий длину 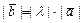 ; 3) направленный одинаково с вектором
; 3) направленный одинаково с вектором 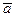 , если
, если 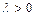 , и противоположно, если
, и противоположно, если 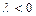 .
.
Ортом вектора 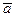 , называется вектор
, называется вектор 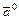 , имеющий единичную длину и направление вектора
, имеющий единичную длину и направление вектора 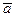 :
: 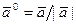 .
.
Базисом в пространстве 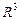 называется упорядоченная тройка некомпланарных векторов, базисом на плоскости
называется упорядоченная тройка некомпланарных векторов, базисом на плоскости 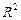 – упорядоченная пара неколлинеарных векторов, базисом на прямой
– упорядоченная пара неколлинеарных векторов, базисом на прямой 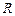 – любой ненулевой вектор на этой прямой. Базис, в котором все векторы попарно перпендикулярны и имеют единичную длину, называется ортонормированным. Векторы ортонормированного базиса обозначаются:
– любой ненулевой вектор на этой прямой. Базис, в котором все векторы попарно перпендикулярны и имеют единичную длину, называется ортонормированным. Векторы ортонормированного базиса обозначаются: 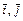 и
и 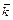 , и называются базисными ортами. Различают правый и левый ортонормированные базисы. Базис
, и называются базисными ортами. Различают правый и левый ортонормированные базисы. Базис 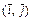 -называется правым, если кратчайший поворот от
-называется правым, если кратчайший поворот от 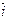 к
к 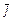 совершается против хода часовой стрелки, в противном случае он – левый. Базис
совершается против хода часовой стрелки, в противном случае он – левый. Базис 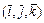 -называется правым, если из конца вектора
-называется правым, если из конца вектора 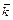 кратчайший поворот от вектора
кратчайший поворот от вектора 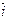 к
к 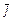 виден совершающимся против хода часовой стрелки, в противном случае он – левый.
виден совершающимся против хода часовой стрелки, в противном случае он – левый.
Условием коллинеарности векторов 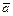 и
и 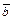 является равенство:
является равенство: 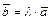 , где
, где 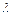 - некоторое число. Условием компланарности векторов
- некоторое число. Условием компланарности векторов 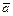 ,
, 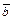 и
и 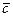 является равенство:
является равенство: 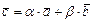 , где
, где 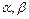 - некоторые числа.
- некоторые числа.
Дата публикования: 2014-11-18; Прочитано: 261 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
