Преобразование матрицы ЦКП к ортогональному виду

Недостаток приведённых выше матриц ЦКП заключается в том, что они не ортогональны.

Ортогональность – это свойство матрицы планирования, которое обеспечивает возможность независимой оценки всех коэффициентов математической модели объекта. Причем ортогональная матрица позволяет после проведения опытов очень просто вычислить любой коэффициент: нужно почленно перемножить столбец матрицы, имеющий одноименный с вычисляемым коэффициентом индекс, и столбец с результатами опытов, сложить эти произведения и сумму разделить на число опытов.

Правило проверки ортогональности матрицы: сумма почленных произведений любых двух столбцов должна равняться нулю.

Нетрудно видеть, что для приведённых выше матриц это условие не соблюдается при перемножении столбца Х₀ с квадратичными столбцами, а также при перемножении квадратичных столбцов друг с другом.

Однако, этот недостаток можно устранить и сделать матрицу ЦКП ортогональной. Для этого надо преобразовать квадраты факторов 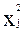и специальным образом выбрать величины звёздного плеча α.

Вместо квадратичных переменных 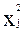нужно ввести в матрицу новые переменны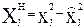е: где 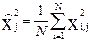- среднее значение квадратичного столбца исходной матрицы. Введение новых переменных обеспечивает ортогональность столбца X₀ с преобразованными квадратичными столбцами.

Для определения условия ортогональности преобразованных квадратичных столбцов между собой, необходимо почленно перемножить эти столбцы и сумму произведений приравнять нулю. В результате получается следующее уравнение:

4α⁴ + 4α²N_я – N_я(N*+1) = 0

Решая это уравнение для ЦКП с различным количеством факторов, можно найти численные значения звёздного плеча α, обеспечивающие ортогональность соответствующих матриц:

Число факторов k
Число опытов в ядре плана
Число звёздных точек
Звёздное плечо α		1,215	1,414	1,547

Рассмотрим применение этого приёма для объекта с двумя факторами (k=2). Обратившись к соответствующей матрице ЦКП, нетрудно подсчитать средние значения квадратичных столбцов при α = 1:

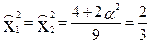
Новые переменные: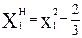

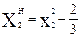
Подставив значения новых переменных вместо квадратичных столбцов, получим преобразованную ортогональную матрицу:

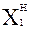
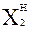
№	X0	X1	X2	X1·X2			Части ЦКП
	+1	+1	+1	+1	+1/3	+1/3	Ядро Nя = 2k
	+1	-1	+1	-1	+1/3	+1/3
	+1	+1	-1	-1	+1/3	+1/3
	+1	-1	-1	+1	+1/3	+1/3
	+1	+1			+1/3	-2/3	Звёздные точки N* = 2k
	+1	-1			+1/3	-2/3
	+1		+1		-2/3	+1/3
	+1		-1		-2/3	+1/3
	+1				-2/3	-2/3	Центр

Теперь выполним преобразование матрицы к ортогональному виду для объекта с тремя факторами.

Обратившись к соответствующей матрице ЦКП, подсчитаем средние значения квадратичных столбцов при α=1,215:

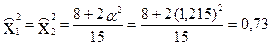
Новые переменные:

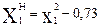
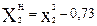
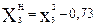
Подставив значения новых переменных вместо квадратичных столбцов, получим преобразованную ортогональную матрицу:

№	X0	X1	X2	X3	X1·X2	X1·X3	X2·X3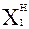
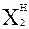
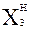
	+1	-1	-1	-1	+1	+1	+1	0,27	0,27	0,27
	+1	+1	-1	+1	-1	+1	-1	0,27	0,27	0,27
	+1	-1	+1	+1	-1	-1	+1	0,27	0,27	0,27
	+1	+1	+1	-1	+1	-1	-1	0,27	0,27	0,27
	+1	-1	+1	-1	-1	+1	-1	0,27	0,27	0,27
	+1	+1	+1	+1	+1	+1	+1	0,27	0,27	0,27
	+1	-1	-1	+1	+1	-1	-1	0,27	0,27	0,27
	+1	+1	-1	-1	-1	-1	+1	0,27	0,27	0,27
	+1	+α						0,746	-0,73	-0,73
	+1	-α						0,746	-0,73	-0,73
	+1		+α					-0,73	0,746	-0,73
	+1		-α					-0,73	0,746	-0,73
	+1			+α				-0,73	-0,73	0,746
	+1			-α				-0,73	-0,73	0,746
	+1							-0,73	-0,73	-0,73

Следует помнить, что ортогональность рассмотренных квадратичных матриц достигнута путём подстановок новых переменных. Поэтому, после проведения опытов и вычисления квадратичных коэффициентов с помощью соответствующих столбцов ортогональной матрицы, нужно будет при написании модели объекта эти квадратичные коэффициенты умножать на указанные ранее выражения.

Затем следует раскрыть скобки, постоянные составляющие сложить с коэффициентом b₀ , оставив квадратичные члены c получившимися при раскрытии скобок числовыми значениями.