 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема. 1. Якщо ранг матриці А дорівнює рангу розширеної матриіці і це спільне значення менше n (rA=r <n)
|
|
1. Якщо ранг матриці А дорівнює рангу розширеної матриіці 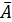 і це спільне значення менше n (rA=r
і це спільне значення менше n (rA=r 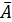 < n), де n – кількість невідомих у системі, то система (1) є невизначеною.
< n), де n – кількість невідомих у системі, то система (1) є невизначеною.
2. Якщо ранг матриці А дорівнює рангу розширеної матриіці 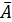 і це спільне значення дорівнює n (rA=r
і це спільне значення дорівнює n (rA=r 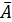 = n), де n – кількість невідомих у системі, то система (1) є визначеною.
= n), де n – кількість невідомих у системі, то система (1) є визначеною.
Доведення. Нехай задано систему
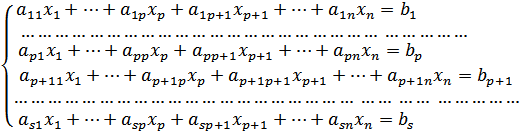
За умовою rA=r 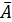 = n
= n


Рівність рангів означає, що в матриці 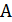 і
і 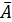 є лише р лінійно незалежних стовпців. Для визначенності, нехай це будуть перші р стовпців. Це також означає, що в матриц
є лише р лінійно незалежних стовпців. Для визначенності, нехай це будуть перші р стовпців. Це також означає, що в матриц 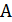 і
і 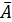 лише р - лінійно-залежних рядків. Нехай для визначенності це будуть перші р - рядків.
лише р - лінійно-залежних рядків. Нехай для визначенності це будуть перші р - рядків. 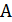 тому мінор р - того порядку, не рівний нулю розташований у лівому верхньому куту. Для системи (1) з попередньої інформаії випливає, що в ній лише р - лінійно незалежних рівнянь, причому за нашим припущенням це перші р з них, а інші s-р рівнянь є їх лінійними комбінаціями, тому за допомогою елементарних перетворень їх можна перетворити на рівняння такого типу
тому мінор р - того порядку, не рівний нулю розташований у лівому верхньому куту. Для системи (1) з попередньої інформаії випливає, що в ній лише р - лінійно незалежних рівнянь, причому за нашим припущенням це перші р з них, а інші s-р рівнянь є їх лінійними комбінаціями, тому за допомогою елементарних перетворень їх можна перетворити на рівняння такого типу 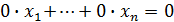 , отже їх можна відкинути.
, отже їх можна відкинути.
В отриманій системі ліворуч запишемо ті невідомі, коефіцієнти при яких утворюютъ визначник р-того порядку, не рівний нулю. За нашим припущенням це перші р. Отже, отримаемо систему
| (4) |
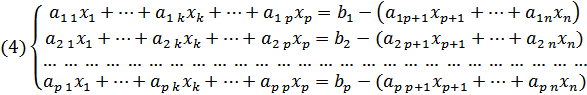 .
.
Будемо розглядати цю систему, як систему р рівнянъ з р невідомими і з визначником, що не дорівнює нулю. Застосуємо теорему Крамера. Тоді матимемо для 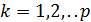 :
:
| (5) |
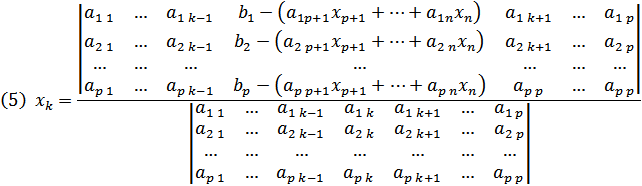
Розглянемо два випадки.
1) Нехай p<n. Тоді існують вільні невідомі 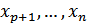 в тому сенсі, що їх можна задавати довільно. Тобто, в цьому випадку система має безліч розв’язків, а тому є невизначеною.
в тому сенсі, що їх можна задавати довільно. Тобто, в цьому випадку система має безліч розв’язків, а тому є невизначеною.
2) Нехай p=n. Покладемо в (5) 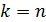 :
:
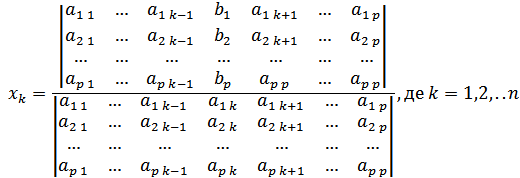
Тобто в цьому випадку вільних невідомих система не має, тому система має один розв’язок, а тому є визначеною.
З формули (5) отримаємо співвідношення (**) для однорідної системи, важливе для наступного розділу.
Означення. Однорідною системою лінійних алгебраїчних рівнянь називається лінійна система, вільні члени якої дорівнюють нулю.
Запишемо формулу (5) для однорідної системи:
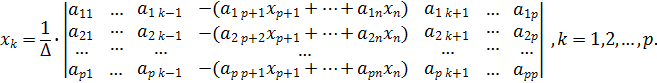
Розкладемо цей визначник за елементами k -того стовбця
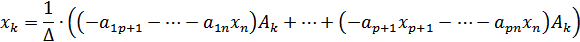
Розкриємо всі дужки, зведемо подібні, тоді отримаємо:
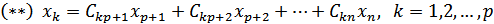 .
.
Дата публикования: 2014-11-18; Прочитано: 1124 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
