 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Распространение волн в реальных металлах
|
|
Для реальных металлов 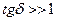 . Поэтому, пренебрегая единицей по сравнению с
. Поэтому, пренебрегая единицей по сравнению с 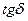 в общих выражениях для
в общих выражениях для 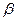 и
и 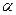 :
:
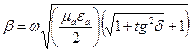 ,
,
 ,
,
для реальных металлов получим:
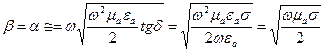 . (1)
. (1)
Учитывая (1), длинна волны в реальных металлах будет определяться выражением:
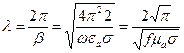 . (2)
. (2)
Характеристическое сопротивление плоской волны в реальных металлах в показательной форме будет иметь вид:
 . (3)
. (3)
Используя формулу Эйлера, соотношение (3) можно переписать в алгебраической форме:
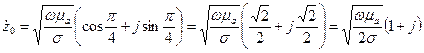 . (4)
. (4)
В приведённой ниже таблице представлены некоторые параметры плоской волны на частоте 1 МГц в вакууме и в меди, наглядно иллюстрирующие особенности распространения в реальных металлах.
Вакуум (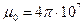 Гн/м, Гн/м,  Ф/м) Ф/м)
| Медь (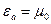 , , 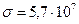 См/м) См/м)
|
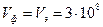 м/с м/с
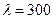 м м
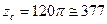 Ом Ом
|  м/с м/с
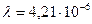 м м
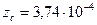 Ом Ом
|
В реальных проводниках электромагнитные волны испытывают значительное ослабление. При распространении в меди на частоте 1 МГц на пути 1 мм уменьшение амплитуды составляет:
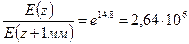 .
.
При распространении волн в реальных проводниках (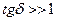 ) общее выражение для глубины проникновения в средах с потерями можно преобразовать следующим образом:
) общее выражение для глубины проникновения в средах с потерями можно преобразовать следующим образом:
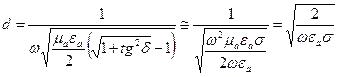 . (5)
. (5)
Из (5) следует что с ростом частоты глубина проникновения уменьшается.
6.6. Поляризация волн.
Для описания ориентации волн в пространстве вводят понятие поляризации. Под плоскостью поляризации подразумевают плоскость, проходящую через направление распространения волны и параллельно вектору 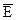 . Из определения следует, что полученные ране решения:
. Из определения следует, что полученные ране решения:
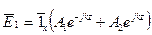 ;
; 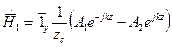 ; (1)
; (1)
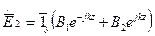 ;
; 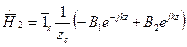 ; (2)
; (2)
- соответствуют двум плоским волнам с взаимно ортогональными плоскостями поляризации.
Рассмотрим основные виды поляризации на примере плоской волны, составляющие которой образованы комбинацией частных решений (1), (2):
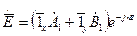 ; (3)
; (3)
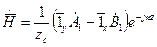 . (4)
. (4)
Пусть слагаемые в соотношениях (3), (4) синфазны: 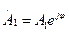 ;
; 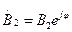 .
.
В этом случае выражение (3) можно преобразовать следующем образом:
 . (5)
. (5)
Переходя в (5) к мгновенным значениям, получим:
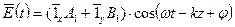 . (6)
. (6)
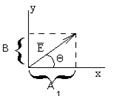 Из (6) следует, что поперечный вектор
Из (6) следует, что поперечный вектор 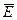 результирующей плоской волны расположен в плоскости, образующей угол
результирующей плоской волны расположен в плоскости, образующей угол  с плоскостью XOZ (см. рис.).
с плоскостью XOZ (см. рис.).
При этом 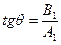 . (7)
. (7)
В процессе распространения волны положение плоскости поляризации остаётся неизменным. Подобную поляризацию называют линейной.
Пусть слагаемые в (3), (4) равны по амплитуде, а по фазе отличаются на -90°:
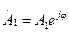 ,
, 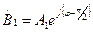 , в этом случае выражение (3) можно привести к виду:
, в этом случае выражение (3) можно привести к виду:
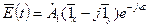 , (8)
, (8)
а временная зависимость 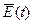 будет определяться соотношением:
будет определяться соотношением:
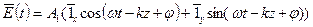 . (9)
. (9)
Тангенс угла  , определяющего положение плоскости поляризации относительно плоскости ХОZ, будет иметь вид:
, определяющего положение плоскости поляризации относительно плоскости ХОZ, будет иметь вид:
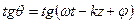 , (10)
, (10)
а сам угол будет определяться выражением:
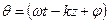 . (11)
. (11)
Из (11) следует, что в этом случае распространение волны сопровождается вращением плоскости поляризации. При этом поперечный вектор 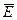 описывает винтообразную кривую на поверхности воображаемого цилиндра.
описывает винтообразную кривую на поверхности воображаемого цилиндра.

Приведённые рисунки иллюстрируют этот процесс при t=const и z=const. При z=const вектор 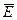 будет вращаться по часовой стрелке, если смотреть в направлении распространения волны, с угловой скоростью
будет вращаться по часовой стрелке, если смотреть в направлении распространения волны, с угловой скоростью 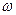 , описывая в плоскости XOY окружность. Такой вид поляризации называют круговой правой. Для получения левой круговой поляризации, при которой вектор
, описывая в плоскости XOY окружность. Такой вид поляризации называют круговой правой. Для получения левой круговой поляризации, при которой вектор 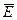 будет вращаться против часовой стрелки, слагаемые в (3) и (4) так же должны быть равны по амплитуде, а по фазе отличаться на 900:
будет вращаться против часовой стрелки, слагаемые в (3) и (4) так же должны быть равны по амплитуде, а по фазе отличаться на 900: 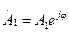 ,
, 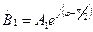 .
.
Из приведенных рассуждений следует, что комбинированное представление составляющих поля (3), (4) будут соответствовать плоской волне с круговой поляризацией, если взаимно ортогональные слагаемые в этих выражениях равны по амплитуде и отличаются по фазе на 900. Нарушение хотя бы одного из условий приведены к эллиптической поляризации. При распространении волны в этом случае поперечный вектор 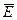 описывает винтообразную кривую на поверхности эллиптического цилиндра, а при z=const, он будет вращаться, описывая эллипс (см. рис.).
описывает винтообразную кривую на поверхности эллиптического цилиндра, а при z=const, он будет вращаться, описывая эллипс (см. рис.).

Степень отличия эллиптической поляризации от круговой характеризуют коэффициентом эллиптичности, который определяют как отношение большой оси поляризационного эллипса к малой.
Раздел 7. Волновые явления на границе раздела двух сред.
7.1. Плоские волны, распространяющиеся произвольном направлении.
В предыдущем разделе рассматривались плоские волны, распространяющиеся вдоль одной из осей – декартовой системы координат. Так, волне распространяющейся в среде без потерь, в положительном направлении оси z, соответствовал фазовый множитель 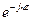 .
.
|
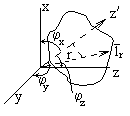
Получим выражение фазового множителя для волны, распространяющейся в направлении 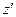 , образующем углы
, образующем углы 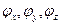 с осями x, y, z декартовой системы (см. рисунок). Выражения для составляющих поля плоской волны в этом случае будут иметь вид:
с осями x, y, z декартовой системы (см. рисунок). Выражения для составляющих поля плоской волны в этом случае будут иметь вид:
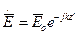 , (1)
, (1)
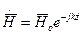
где 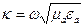 ,
, 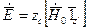 ,
, 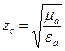 .
.
Единичный вектор в направлении Z` связан с ортами декартовой системы соотношением: ̅1z`= ̅1x cos φx + ̅1y cos φy + ̅1z cos φz
Поверхность равных фаз плоской волны определяется выражением: 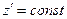 . Проекции произвольного радиус вектора
. Проекции произвольного радиус вектора 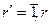 , проведенного из начала координат до пересечения с фазовой поверхностью будут определяться соотношением:
, проведенного из начала координат до пересечения с фазовой поверхностью будут определяться соотношением:
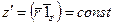
 . (3)
. (3)
Радиус-вектор 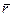 можно выразить через его проекции следующим образом:
можно выразить через его проекции следующим образом:
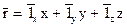 . (4)
. (4)
Подставляя (2), (4) в скалярное произведение (3), получим:
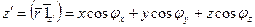 . (5)
. (5)
Используя (5), соотношения (1) можно переписать в виде:
 , (6)
, (6)
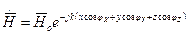 .
.
Таким образом, фазовый множитель плоской волны, распространяющейся в произвольном направлении, определяемом углами 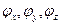 в декартовой системе координат представляется в виде:
в декартовой системе координат представляется в виде: 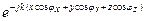 . Тригонометрические функции в показателе экспоненты принято называть направляющими косинуса.
. Тригонометрические функции в показателе экспоненты принято называть направляющими косинуса.
При распространении волны в среде с потерями в полученном выражении фазового множителя волновое число  следует заменить комплексной постоянной распространения g =b — ja.
следует заменить комплексной постоянной распространения g =b — ja.
7.2. Падение плоской волны на границу раздела двух сред.
Вводное замечание.
|
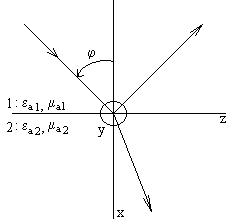
Рассмотрим наклонное падение плоской волны на плоскую границу раздела двух сред. Среды без потерь и характеризуются параметрами: 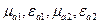 .Угол между направлением распространения падающей волны и нормалью к границе раздела называют углом падения. Плоскость, проходящую через нормаль к границе раздела и параллельную направлению распространения падающей волны называют плоскостью падения. Вектор
.Угол между направлением распространения падающей волны и нормалью к границе раздела называют углом падения. Плоскость, проходящую через нормаль к границе раздела и параллельную направлению распространения падающей волны называют плоскостью падения. Вектор 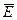 падающей волны перпендикулярен направлению распространения, а относительно плоскости падения он может быть ориентирован под произвольным углом. В этих случаях вектор
падающей волны перпендикулярен направлению распространения, а относительно плоскости падения он может быть ориентирован под произвольным углом. В этих случаях вектор 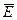 падающей волны удобно представить суперпозицией двух волн: с вектором электрического поля перпендикулярным и параллельным плоскости падения:
падающей волны удобно представить суперпозицией двух волн: с вектором электрического поля перпендикулярным и параллельным плоскости падения: 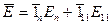 . Первый случай называют нормальной поляризацией, второй – параллельной.
. Первый случай называют нормальной поляризацией, второй – параллельной.
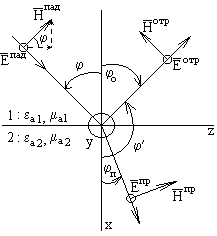
Введём декартову систему координат так, чтобы плоскость YOZ совпадала с границей раздела сред, а плоскость XOZ - с плоскостью падения (см. рис.). Угол падения отсчитывается от оси X. Углы между направлением распространения падающей волны и осями декартовой системы равны: 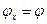 ,
, 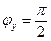 ,
, 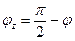 , а направляющие косинусы будут определяться соотношениями:
, а направляющие косинусы будут определяться соотношениями: 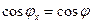 ,
, 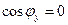 ,
, 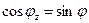 . Таким образом, фазовый множитель поля падающей волны будет иметь вид:
. Таким образом, фазовый множитель поля падающей волны будет иметь вид:
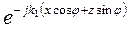 ,
,
где 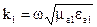 .
.
Нормальная поляризация.
|
В качестве частной задачи рассмотрим наклонное падение плоской нормально поляризованной волны на плоскую границу раздела сред с параметрами: 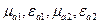 . Введем декартову систему координат, совместив плоскость YOZ с границей раздела сред, а плоскость XOZ – с плоскостью падения. Вектор
. Введем декартову систему координат, совместив плоскость YOZ с границей раздела сред, а плоскость XOZ – с плоскостью падения. Вектор 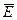 падающей волны ориентирован в положительном направлении оси Y. Вектор
падающей волны ориентирован в положительном направлении оси Y. Вектор  падающей волны расположен в плоскости падения и его проекции определяются из векторного треугольника, приведенного на рисунке.
падающей волны расположен в плоскости падения и его проекции определяются из векторного треугольника, приведенного на рисунке.
С учетом сделанных замечаний составляющие поля падающей волны будут иметь вид:
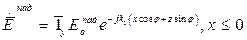 ; (1)
; (1)
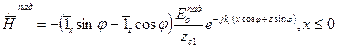 , (2)
, (2)
где 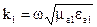 ;
; 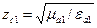 .
.
В общем случае, при падении волны на границу раздела сред образуются отраженная и преломленная волны. Будем полагать, что в данном случае (см. рисунок) направления распространения отраженной и преломленной волн лежат в плоскости падения падающей волны и, так же как и падающая полна, они – нормально поляризованы. Направления распространения отраженной и преломленной волн определяются соответственно углами 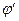 и
и  , отсчитываемыми от оси X (см. рисунок).
, отсчитываемыми от оси X (см. рисунок).
По аналогии с (1), (2) выражения для составляющих поля отраженной и преломленной волн можно представить в виде:
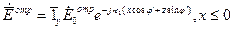 ; (3)
; (3)
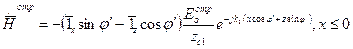 ; (4)
; (4)
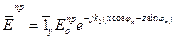 ,
, 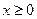 ; (5)
; (5)
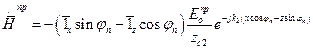 ,
, 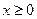 , (6)
, (6)
где 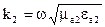 ,
, 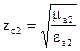 .
.
В данном случае известными полагаются электродинамические параметры сред: 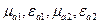 и характеристики падающей волны:
и характеристики падающей волны: 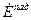 ,
, 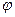 . Требуется определить характеристики отраженной и преломленной волн:
. Требуется определить характеристики отраженной и преломленной волн:  ,
, 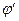 ,
, 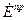 ,
,  . Если удастся получить решения, удовлетворяющие граничным условиям:
. Если удастся получить решения, удовлетворяющие граничным условиям:
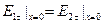 ;
;  , (7)
, (7)
то в соответствии с теоремой единственности они будут достоверными и единственно возможными.
Учитывая, что поле в первой среде является результатом наложения падающей и отраженной волн, а во второй среде совпадает с полем преломленной волны, то, подставляя (1), (2), (3), (4), (5) и (6) в (7), получим соотношения:
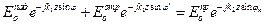 , x=0, (8)
, x=0, (8)
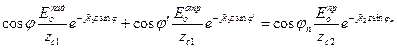 ,x=0, (9)
,x=0, (9)
которые будут выполняться во всех точках границы раздела и при любых значениях координаты z. Это возможно, если слагаемые в этих соотношениях имеют одинаковую функциональную зависимость по z. При этом должны выполняться следующие равенства:
 , (10)
, (10)
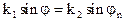 . (11)
. (11)
Учитывая, что пределы изменения углов 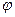 и
и 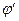 определяются неравенствами:
определяются неравенствами:  ,
, 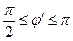 , из (10) следует
, из (10) следует
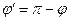 . (12)
. (12)
Направление распространения отраженной волны удобно задавать с помощью угла 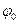 (см. рисунок), называемого углом отражения, и дополняющего угол
(см. рисунок), называемого углом отражения, и дополняющего угол 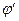 до
до 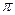 :
:
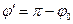 . (13)
. (13)
Подставляя (13) в (12), получим:
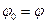 . (14)
. (14)
Равенство (14) называют – первым законом Снелиуса.
Соотношение (11) можно переписать следующим образом:
 . (15)
. (15)
Преобразую (15), получим равенство:
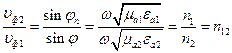
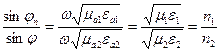 ;
; 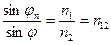 , (16)
, (16)
где n12 – относительный показатель преломления. Соотношение (16) называют – вторым законом Снелиуса.
Таким образом, с помощью выражений (14), (16) решается задача определения направлений распространения отраженной и преломленной волн. Для расчета их амплитуд преобразуем уравнения (8), (9): равенства (10), (11) позволяют сократить фазовые множители, а выражение (12) – выполнить замену 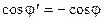 . Преображенные уравнения будут иметь вид:
. Преображенные уравнения будут иметь вид:
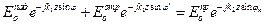 , x=0; (17)
, x=0; (17)
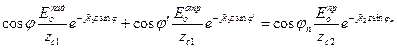 , x=0. (18)
, x=0. (18)
Введем понятия коэффициентов отражения и преломления по электрическому полю при нормальной поляризации:
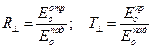 . (19)
. (19)
С учетом (19) уравнения (17), (18) можно переписать в виде
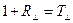 , (20)
, (20)
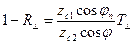 . (21)
. (21)
Решая систему (20), (21) относительно 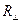 и
и 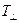 , получим выражения:
, получим выражения:
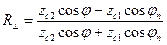 ;
;  , (22)
, (22)
которые с помощью (19) по известной амплитуде падающей волны позволяют определить амплитудные значения отраженной и преломленной волн. Используя (15), в соотношениях (22)  можно исключить, выразив его через функционал от
можно исключить, выразив его через функционал от 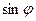 :
:
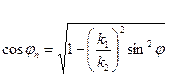 . (23)
. (23)
Полностью определив характеристики отраженной и преломленной волн, получим выражения для результирующего поля в первой и второй средах.
Поле в первой среде представляет собой композицию падающей и отраженной волн:
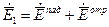 ;
; 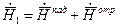 . (24)
. (24)
Подставляя в (24) соотношения (1)-(4), используя (19) и, учитывая, что 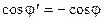 и
и 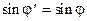 , получим:
, получим:
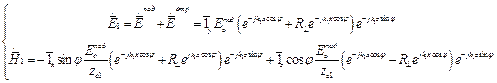 ,
,  , (25),(26)
, (25),(26)
Поле во второй среде формируется преломленной волной:
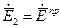 ;
; 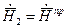 . (27)
. (27)
Подставляя в (27) соотношения (5), (6), получим:
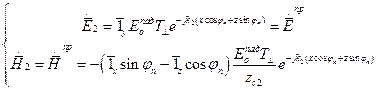 ,
, 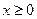 , (28), (29)
, (28), (29)
Коэффициенты отражения и преломления: 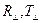 (иногда их называют коэффициентами Френеля) были получены для сред без потерь. Но соотношения (22) остаются справедливыми и в том случае, если одна из сред или обе среды обладают проводимостью отличной от нуля.
(иногда их называют коэффициентами Френеля) были получены для сред без потерь. Но соотношения (22) остаются справедливыми и в том случае, если одна из сред или обе среды обладают проводимостью отличной от нуля.
Параллельная поляризация.
|
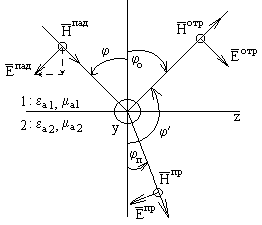
Пусть вектор 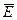 падающей волны находится в плоскости падения, а вектор
падающей волны находится в плоскости падения, а вектор  - ориентирован в положительном направлении оси Y (см. рисунок). Используя рассуждения аналогичные приведённым выше, составляющие поля падающей, отраженной и преломленной волн в этом случае можно записать в виде:
- ориентирован в положительном направлении оси Y (см. рисунок). Используя рассуждения аналогичные приведённым выше, составляющие поля падающей, отраженной и преломленной волн в этом случае можно записать в виде:
 , х £ 0 (1)
, х £ 0 (1)
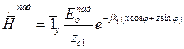 , х £ 0, (2)
, х £ 0, (2)
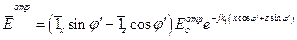 , х £ 0, (3)
, х £ 0, (3)
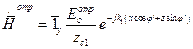 , х £ 0, (4)
, х £ 0, (4)
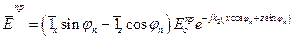 , х ³ 0, (5)
, х ³ 0, (5)
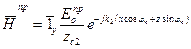 , х ³ 0, (6)
, х ³ 0, (6)
Так же как в предыдущем разделе, неизвестными являются характеристики отраженной и преломленной волн: 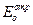 ,j¢,
,j¢, 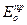 , jn. Их значения найдем, решая граничные задачи:
, jn. Их значения найдем, решая граничные задачи:
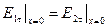 ;
;  . (7)
. (7)
Из построений приведенных на рисунке следует, что равенства (7) можно записать следующим образом:
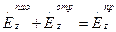 , х = 0, (8)
, х = 0, (8)
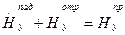 , х = 0. (9)
, х = 0. (9)
Подставляя (1), (2), (3), (4), (5) и (6) в (8), (9), получим:
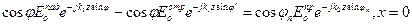 , (10)
, (10)
 , (11)
, (11)
Граничные условия (10), (11) остаются справедливыми при произвольных значениях координаты z. При этом, как при нормальной поляризации, должны выполняться равенства:
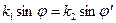 (12)
(12)
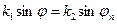 (13)
(13)
Из (12), (13) следует инвариантность законов Снелиуса относительно поляризации поля падающей волны (см. предыдущей раздел). Используя (12), (13), и, вытекающие из (12), равенства 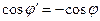 ,
, 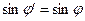 , приведем уравнения (10), (11) к виду:
, приведем уравнения (10), (11) к виду:
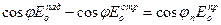 , (14)
, (14)
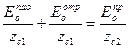 . (15)
. (15)
Введем понятие коэффициентов отражения и преломления по полю при параллельной поляризации:
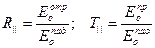 . (16)
. (16)
С помощью (16) уравнения (14), (15) можно записать следующим образом:
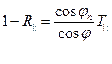 , (17)
, (17)
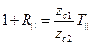 . (18)
. (18)
Решая систему (17), (18) относительно коэффициентов 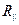 и
и 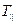 :
:
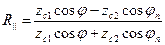 ;
; 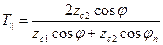 , (19)
, (19)
- получим коэффициенты Френеля для параллельной поляризации.
Как и в предыдущем разделе, в выражениях (19)  можно заменить функционалом от
можно заменить функционалом от 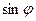 .
.
Из сравнения формул для коэффициентов Френеля при нормальной поляризации следует их поляризованная зависимость.
Так же как в предыдущем разделе, использую (1)-(6), (12), (13), (16), получим соотношения для результирующего поля в первой и второй средах при параллельной поляризации:
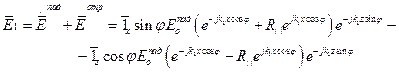 , х £ 0 (20)
, х £ 0 (20)
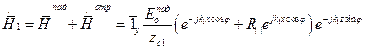 , х £ 0 (21)
, х £ 0 (21)
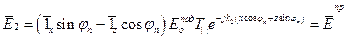 , х ³ 0 (22)
, х ³ 0 (22)
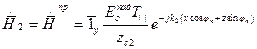 , х ³ 0 (23)
, х ³ 0 (23)
Падение плоской волны по нормали к границе раздела сред. В этом случае 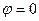 и понятие плоскости падения теряет свой смысл. При этом
и понятие плоскости падения теряет свой смысл. При этом 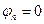 и выражения для коэффициентов Френеля можно упростить:
и выражения для коэффициентов Френеля можно упростить:
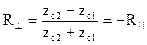 ;
; 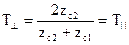 .
.
Дата публикования: 2014-11-19; Прочитано: 435 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
