 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Непрерывные случайные величины и их характеристики
|
|
Если значение, которые может принимать данная случайная величина 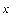 , заполняет целый конечный или бесконечный промежуток
, заполняет целый конечный или бесконечный промежуток 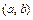 числовой оси, то случайная величина называется непрерывной.
числовой оси, то случайная величина называется непрерывной.
Непрерывную случайную величину невозможно задать с помощью ряда или многоугольника распределения, потому что множество ее возможных значений бесконечно.
Для характеристики непрерывной случайной величины целесообразно использовать не вероятность события 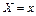 , а вероятность события
, а вероятность события 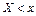 , где
, где 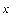 — некоторое действительное число.
— некоторое действительное число.
Если 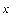 изменяется произвольно, то вероятность выполнения неравенства
изменяется произвольно, то вероятность выполнения неравенства 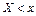 в общем случае будет изменяться.
в общем случае будет изменяться.
Итак, 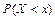 является функцией аргумента
является функцией аргумента 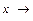
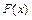 .
.
Функцией распределения непрерывной случайной величины 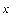 называется функция
называется функция 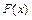 , которая задает вероятность того, что случайная величина Х примет значение, меньше чем
, которая задает вероятность того, что случайная величина Х примет значение, меньше чем 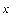 , то есть
, то есть
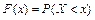 .
.
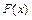 называют интегральной функцией распределения.
называют интегральной функцией распределения.
Непрерывную случайную величину можно задать также с помощью функции, которая называется плотностью распределения.
Дифференциальной функциейраспределенияили плотностью распределения вероятностей называется первая производная интегральной функции распределения, то есть 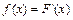 .
.
График дифференциальной функции распределения 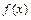 называется кривой распределения. Вероятность того, что в результате испытания случайная величина получит значение, которые принадлежит интервалу
называется кривой распределения. Вероятность того, что в результате испытания случайная величина получит значение, которые принадлежит интервалу 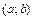 , можно найти по формуле:
, можно найти по формуле:
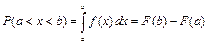 .
.
Геометрически вероятность попадания случайной величины в промежуток 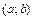 равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью 0 х и прямыми
равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью 0 х и прямыми 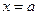 ,
, 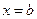 .
.
 |
Свойства плотности распределения 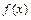 :
:
1) 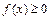 , для всех
, для всех 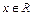 ;
;
2) 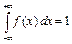 ;
;
3) 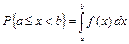 ;
;
4) 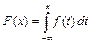 .
.
Если случайная величина Х определена в интервале 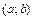 , а
, а 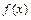 — функция плотности распределения вероятности, то
— функция плотности распределения вероятности, то
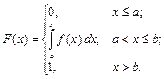
Математическим ожиданием 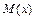 непрерывной случайной величины Х, возможные значения которой принадлежат отрезку
непрерывной случайной величины Х, возможные значения которой принадлежат отрезку 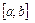 , называется определенный интеграл
, называется определенный интеграл
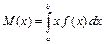 .
.
Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения
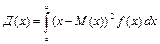 .
.
Для вычисления дисперсии непрерывной случайной величины используют более удобную формулу
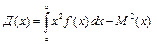 .
.
Среднее квадратичное отклонение непрерывной случайной величины, как и для величины дискретной, определяется равенством
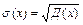 .
.
Начальный теоретический момент порядка 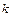 непрерывной случайной величины
непрерывной случайной величины 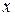 определяется равенством:
определяется равенством:
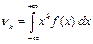 .
.
Центральный теоретический момент порядка 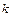 непрерывной случайной величины
непрерывной случайной величины 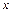 определяется равенством:
определяется равенством:
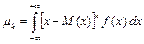 .
.
Если все возможные значения 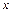 принадлежат интервалу
принадлежат интервалу 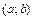 , то
, то
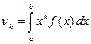 ;
; 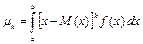 .
.
Центральные моменты выражаются через начальные моменты формулами:
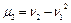 ;
;
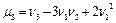
и т.д.
Центральный момент третьего порядка характеризует асимметрию распределения, то есть асимметрией называется отношение центрального момента 3-го порядка к кубу среднего квадратичного отклонения:
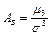 .
.
Центральный момент четвертого порядка характеризует эксцесс (крутизна)распределения и выражается равенством
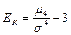 .
.
Дата публикования: 2014-11-19; Прочитано: 1004 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
