Зв’язок методу Гаусса з розкладанням матриці на множники

Алгоритм методу вилучення Гаусса можна компактно записати в матричних позначеннях. Він відповідає розкладанню матриці А на добуток більш простих матриць. Є дві модифікації алгоритму матричного вилучення. Одна з них полягає в зведені початкової матриці до трикутної, на діагоналі у якої стоять одиниці (цей випадок розглянуто вище), а друга, коли на діагоналі стоять провідні елементи.

Спочатку для наочності розглянемо систему 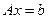, що складається з трьох рівнянь:

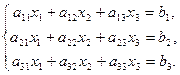(19)

Вилучення невідомої з двох останніх рівнянь системи (19) здійснюється виконанням таких операцій:

· ділення першого рівняння на елемент ;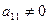

· віднімання перетвореного першого рівняння, помноженого на , від рівнянь .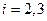

Перша операція еквівалентна множенню системи рівнянь зліва на діагональну матрицю

;

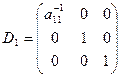друга операція еквівалентна множенню системи рівнянь зліва на матрицю

.

Звідси випливає, що виключення рівносильно множенню системи зліва на матрицю, яку називають елементарною нижньою трикутною матрицею. Дві розглянуті операції можна об’єднати, ввівши до розгляду матрицю 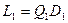, яка має вигляд

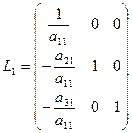. (20)

Перетворимо за допомогою матриці 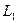початкову систему, тобто запишемо її у вигляді 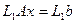. У результаті отримаємо систему

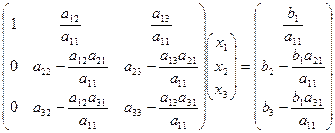. (21)

Перепишемо її у вигляді

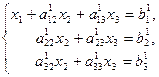(22)

і виконаємо другий крок методу Гаусса, тобто вилучимо невідому 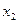останнього рівняння. Це виконується множенням системи (16) зліва на елементарну матрицю :

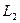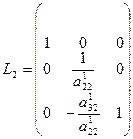. (23)

У результаті отримаємо систему рівнянь

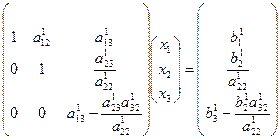. (24)

Таким чином, після другого кроку вилучення приходимо до системи 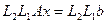, яку в спрощеному вигляді можна записати так:

. (25)

Нарешті, помноживши (19) на матрицю

,

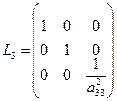одержимо систему 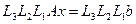у якої матриця 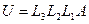є верхньою трикутною матрицею з одиничною головною діагоналлю. У розгорнутому вигляді ця система має вигляд

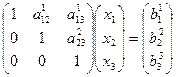. (26)

Зауважимо, що для розв’язання системи (26) достатньо виконати зворотний хід методу Гаусса, який описаний вище.

Розглянемо матрицю 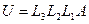. З цієї рівності можна виразити матрицю А у вигляді

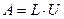, (27)

де 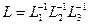– нижня трикутна матриця. Отже, 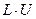– розклад матриці А можна отримати за допомогою елементарних трикутних матриць у такий спосіб: спочатку будують матриці 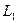, , 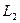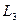і обчислюють матрицю 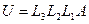, а потім знаходять матрицю 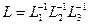. Відзначимо, обернені матриці 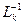мають простий вигляд:

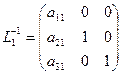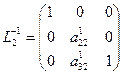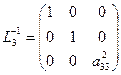, , . (28)

При цьому матриця є нижньою трикутною матрицею:

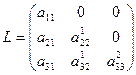, (29)

на головній діагоналі якої розташовані ведучі елементи методу виключення.