Средняя арифметическая взвешенная

Среднее значение по ряду распределения заданного вариантами хi и частотами fi
Частоты отдельных вариантов могут быть выражены относительными величинами – частостями (wi).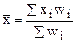

Например, средняя урожайность – взвешивание производиться по площади посевов, а не по количеству участков.

Средняя арифметическая взвешенная интервального ряда распределения вычисляется по правилу:

1) в каждом варианте определить срединное значение 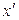, как полусумму значений нижней и верхней границ интервала 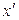=(х0+х1)/2, т.е. образуем дискретный ряд;

2) произвести взвешивание и вычислить среднее .

Мы предположили, что отдельные варианты равномерно распределены внутри интервала, что позволило нам образовать дискретный ряд с вариантами 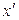=(х0+х1)/2.

Свойства средней арифметической.

1. Если все веса (f) увеличить или уменьшить в одинаковое число раз К, то величина средней не изменится

.

2. Если каждую варианту (х_i) увеличить или уменьшить на одну и ту же величину А, то средняя увеличится или уменьшится на эту же величину

.

3. Если каждую варианту () увеличить или уменьшить в одно и то же число раз (h), то средняя увеличится или уменьшится в то же число раз

.

4. Сумма отклонений вариант от средней, взвешенных их частотами, равна нулю

.

Способ моментов (способ отсчета от условного нуля). С учетом этих свойств формула средней арифметической взвешенной будет иметь вид

.

Здесь – момент 1-го порядка; А – одна из центральных вариант ряда.

Пример 1. Дан интервальный ряд распределения предприятий торговли по объему товарооборота. Найти средний объем товарооборота.

Группы предпр. По Объему Товарообор., х	Число предпр. f	Серед. зн-ние интервала,
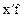
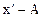
до 400 400-500 500-600 600-700 свыше 700				-200 -100	-2 -1	-18 -12
Итого						-17

Открытые интервалы дополнили до закрытых и рассчитали серединное значение для каждого интервала. Промежуточные расчеты приведены в таблице.

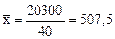млн. руб.;

Расчет средней арифметической способом моментов. А = 550.

млн. руб.

Пример 2. Имеются следующие данные о продаже товара. Рассчитать среднюю цену реализации.

	Город	Цена,	Сумма реализацииwi =fi´xi.	Частота,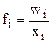
	А Б В
	Итого	–

Рассчитаем среднюю цену реализации по формуле средней гармонической взвешенной. Количество реализованных единиц – частота (f)

руб.

2. Средняя гармоническая используется, когда статистическая информация не содержит частот (f_i) по отдельным вариантам (x_i) совокупности, а представлена как их произведение (f_i´x_i), т.е. в виде объема явления w_i =f_i´x_i. Тогда среднее значение можно вычислить как среднее гармоническое взвешенное

.

Объемы явления w_i =f_i´x_i можно выражать в долях и процентах, формула вычисления остается неизменной. При равных значениях объемов w₁ = w₂ =… w_n средняя вычисляется, как средняя гармоническая простая .

Пример. Средняя цена яблок .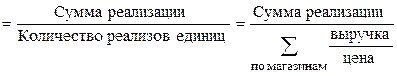

3. Средняя геометрическая – используется как средняя относительных величин динамики, построенных в виде цепных величин (отношения текущего к предыдущему уровню) в рядах динамики (например, в расчетах среднегодовых темпов роста).

Средняя геометрическая простая , где П – символ произведений; n – число вариантов (коэффициент прироста национального дохода).