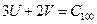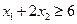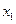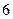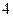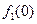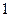|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Учебное пособие. ПО изучению дисциплины
|
|
по изучению дисциплины
«МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ»
Раздел «Задачи многокритериальной оптимизации»
Для студентов ФМК специальности 080507 «Менеджмент организации» и
ФУП специальности 080502 «Экономика и управление на предприятии (социально-культурной сферы)» дневного, вечернего и заочного отделений
Санкт-Петербург
Составители: Брыкин Л.В., профессор
Веселова С.В., доцент
Шутов В.И., доцент
Погонышева В.Н., доцент
Волчанинов В.В., доцент
Рецензенты: Медведев Г.Ф., к.э.н., профессор СПбГУКиТ,
Большакова Л.В.. к.ф.-м.н., профессор университета МВД
Учебное пособие по изучению дисциплины «Математические методы принятия решений». Раздел «Задачи многокритериальной оптимизации» / составители: Брыкин Л.В., Веселова С.В., Шутов В.И., Погонышева В.Н., Волчанинов В.В. – СПб.: СПбГУКиТ, 2008. – 29с.
В учебном пособии рассмотрена классификация задач принятия решений, а так же методы решения задач с несколькими показателями эффективности. Пособие предназначено для студентов ФМК специальности 080507 «Менеджмент организации» и ФУП специальности 080502 «Экономика и управление на предприятии (социально-культурной сферы)».
Рекомендовано к изданию в качестве учебного пособия кафедрой математического моделирования.
Протокол № 6 от 29.01.2008г.
© СПбГУКиТ, 2008
ВВЕДЕНИЕ
Традиционный курс математики несколько формально подходит к изучаемому предмету. Основные принципы математики и необходимость строго анализа составляют лишь часть средств, необходимых в практической деятельности.
Проникновение математических методов в самые разнообразные сферы человеческой деятельности означает возможность пользоваться новыми средствами исследования.
В наше время, которое по справедливости называют эпохой научно-технической революции, наука уделяет все большее внимание вопросам организации и управления. Причин этому много. Быстрое развитие и усложнение техники, небывалое расширение масштабов проводимых мероприятий и спектра их возможных последствий, внедрение автоматизированных систем управления (АСУ) во все области практики – все это приводит к необходимости анализа сложных целенаправленных процессов под углом зрения их структуры и организации. От науки требуются рекомендации по оптимальному управлению такими процессами.
Возможным решением проблемы является дисциплина, главная цель которой – изучение методов постановки математических задач, возникающих в реальных практических ситуациях и методов принятия решений для этих задач. Общее название такого подхода – математическое моделирование.
Математическое моделирование – это искусство применения математики. Другими словами – это применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности. Дисциплина «Математические методы принятия решений» является прикладной математической дисциплиной. А прикладная математика – это использование для описания реального мира любой математической дисциплины, например, статистики, исследования операций, численного анализа или вычислительной математики.
Необходимость принятия решений так же стара, как само человечество. Несомненно, уже в доисторические времена первобытные люди, отправляясь, скажем, охотиться на мамонта, должны были принимать те или другие решения: в каком месте устроить засаду? Как расставить охотников? Чем их вооружить? И т.д. В повседневной жизни, сами того не замечая, люди на каждом шагу принимаем решения. Например, выходя утром из дому, что бы идти на работу, мы должны принять целый ряд решений: как одеться? Брать ли с собой зонтик? В каком месте перейти улицу? Каким видом транспорта воспользоваться? И т.д. Руководитель предприятия то же должен постоянно принимать решения типа: как распорядиться имеющейся рабочей силой? Какие типы работ выполнить в первую очередь? И т.д.
Однако математические методы принятия решений начинаются тогда, когда для обоснования решений применяется тот или другой математический аппарат. До поры до времени решения в любой области практики принимаются без специальных математических расчетов, просто на основе опыта и здравого смысла. Скажем для решения вопроса о том, как одеться, выходя на улицу, и где ее перейти, математика не нужна, да и вряд ли потребуется в дальнейшем. Оптимизация таких решений происходит как бы сама собой, в процессе жизненной практики.
Но бывают решения более ответственные. Например, организация работы общественного транспорта в новом городе с сетью предприятий, жилыми массивами и т.д. Необходимо принять ряд решений: по каким маршрутам, и какие транспортные средства направить? В каких пунктах сделать остановки? Как изменить частоту следования машин в зависимости от времени суток? И т.д. Эти решения – гораздо сложнее, а главное, от них очень многое зависит. Неправильный их выбор может отразиться на деловой жизни целого города. Конечно, и в этом случае при выборе решения можно действовать интуитивно, опираясь на опыт и здравый смысл. Но гораздо разумнее будут решения, если они подкреплены математическими расчетами. Эти предварительные расчеты помогут избежать длительного и дорогостоящего поиска нужного решения «на ощупь».
Возьмем более яркий пример. Пусть речь идет о каком-то крупномасштабном мероприятии – скажем, об отведении части стока северных рек в засушливые зоны. Допустимо ли здесь произвольное, «волевое» решение, которое может привести к серьезным отрицательным последствиям, или же необходима серия предварительных расчетов по математическим моделям? Думается, что здесь двух мнений быть не может – необходимость тщательных, многосторонних расчетов очевидна. «Семь раз отмерь, один – отрежь», - говорит пословица. Математические методы принятия решений и есть своеобразное математическое «примеривание» будущих решений, позволяющее экономить время, силы и материальные средства, избегать серьезных ошибок, на которых уже нельзя «учиться» (слишком дорого это обходится).
С течением времени доля задач, где для выбора решения применяются математические методы, постоянно растет. С ростом масштабов и сложности мероприятий, методы принятия решений приобретают все большую роль. Работа небольшого аэродрома вполне может быть обеспечена силами одного опытного диспетчера; работа крупного аэропорта требует автоматизированной системы управления, работающей согласно четному алгоритму. Выработка такого алгоритма всегда основывается на предварительных расчетах, т.е. на математических методах принятия решений.
Основные характерные черты математических методов принятия решений
Рассмотрим основные характерные черты математического моделирования.
Математик Холл сказал, что целью прикладной математики является математическое осмысление действительности. Но на практике важно получить конкретный ответ на конкретный вопрос, а не стремиться к более возвышенным целям.
Исходным пунктом часто является некоторая эмпирическая ситуация, выдвигающая перед исследователем «задачу», на которую требуется найти «ответ». Прежде всего, необходимо установить, в чем именно заключается «задача». Процесс выделения «задачи», поддающейся математическому анализу, часто бывает продолжительным и требует владения многими навыками, не имеющими отношения к математике.
Часто параллельно с этой стадией подготовки задачи идет процесс выявления основных существенных особенностей явления (см. рис.1).
 |




 Реальная Постановка Модель Прогноз
Реальная Постановка Модель Прогноз



 Ситуация задачи
Ситуация задачи
 | |||||
 | |||||
 | |||||


Проверка Непротиворечивость
адекватности
Рис. 1
После того как существенные факторы выявлены, следующий шаг состоит в переводе этих факторов на язык математических понятий и величин и установление соотношений между этими величинами. Как правило, это самая трудная стадия процесса моделирования.
После построения модели ее следует подвергнуть проверке. В действительности адекватность модели до некоторой степени проверяется обычно в ходе постановки задачи.
Существует несколько аспектов проверки адекватности. Во-первых, сама математическая основа модели должна быть непротиворечивой и подчиняться всем обычным законам математической логики. Во-вторых, справедливость модели зависит от ее способности адекватно описывать исходную ситуацию.
Модель можно заставить отображать действительность, однако, она не сама действительность.
Решение вопроса об адекватности модели сводится к вопросу: достаточно ли хорошо для целей рассматриваемой задачи, результаты, полученные на основе этой модели, отражают положение дел.
Ситуации моделируют для разных целей. Главная из них – необходимость предсказывать новые результаты или новые свойства явления. Часто они относятся к условиям, которые по всей вероятности, будут иметь место в некоторый момент в будущем. В некоторых случаях достаточно уметь описывать математическими средствами работу системы. Обычно при таком описании не учитывается элемент контроля, однако, в моделях, построенных для исследования работы сетей, таких как схемы движения поездов или самолетов, контроль является важным фактором. Многие модели в исследовании операций или технике созданы с целью, облегчить администрации процесс принятия решений.
Математическая модель представляет собой упрощение реальной ситуации. При этом исходная сложная задача сводится к идеализированной задаче, поддающейся математическому анализу. Именно при таком подходе в классической прикладной математике возникли блоки без трения, невесомые нерастяжимые нити, невязкие жидкости и многие другие понятия подобного рода. Эти понятия не существуют в реальной действительности, они являются абстракциями, составной частью идеализации, предпринятой автором модели. И тем не менее, их часто можно с успехом считать хорошим приближением к реальным ситуациям.
Математическая модель, отображающая тот или иной процесс, представляется в виде определенных математических соотношений, которые устанавливают взаимосвязь между параметрами исследуемого процесса. При этом используются как теоретические методы, так и необходимые экспериментальные данные. Конечной целью разработки математических моделей является прогноз результатов проведения процесса и выработка рекомендации по возможным воздействиям на ход процесса с целью ведения его в оптимальных условиях. При отсутствии достаточной информации об исследуемых явлениях их изучение начинается с построения простейших моделей, но без нарушения основной (качественной) специфики исследуемого процесса.
Важнейшее решение, которое часто принимается в самом начале процесса моделирования, касается природы рассматриваемых математических переменных. По существу они делятся на два класса. В один из них входят известные характеристики, т.е. величины, поддающиеся точному измерению и управлению (по крайней мере, теоретически); они называются детерминированными переменными. А сам детерминированный процесс характеризуется непрерывным изменением определяющих величин по вполне определенным закономерностям, при этом выходные величины однозначно определяются входными. В другой класс входят неизвестные характеристики, т.е. величины, которые никогда не могут быть точно измерены и имеют случайный характер; они называются стохастическими переменными. Стохастический процесс характеризуется беспорядочным, часто дискретным изменением определяющих величин, при этом значения выходной величины не находится в соответствии с входной. Модель, содержащая стохастические переменные описывается с помощью теории вероятностей и статистики; детерминированные переменные часто требуют обычного математического анализа. Природа некоторых ситуаций, бывает ясна не сразу, другие ситуации характеризуются переменными обоих типов. Для построения модели чрезвычайно важно, чтобы природа переменных была правильно установлена.
Теперь перейдем к вопросу об интерпретации вытекающих из модели выводов.
Сначала необходимо сделать обратный перевод с математического языка на язык, на котором первоначально формулировалась исходная задача. При этом следует отчетливо осознавать как математический смысл полученных решений, так и то, что они означают на языке реального мира, который математика призвана описывать.
Искусством построения моделей можно овладеть только в результате собственной практики, однако, почувствовать, в чем состоит это искусство, можно разбирая примеры, которые тем или иным образом иллюстрируют различные особенности процесса моделирования.
Разновидности моделей задач принятия решений
Создание математической модели самая важная и ответственная часть исследования, требующая глубокого знания не столько математики, сколько существа моделируемых явлений. Для применения количественных методов исследования в любой области всегда требуется какая-то математическая модель. При построении модели реальное явление неизбежно упрощается, схематизируется, и эта схема описывается с помощью того или другого математического аппарата.
Общих способов построения математических моделей не существует. В каждом конкретном случае модель выбирается исходя из вида операции, ее целевой направленности, с учетом задачи исследования.
Математическая модель должна отражать важнейшие черты явления, все существенные факторы, от которых в основном зависит успех операции. Искусство строить математические модели есть именно искусство, и опыт в нем приобретается постепенно.
В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки.
Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений.
Статистические модели, по сравнению с аналитическими более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое число факторов. Но у них свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений.
Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей.
Задачи принятия решений делятся на две категории: прямые и обратные.
Прямые задачи отвечают на вопрос: что будет, если в заданных условиях, мы примем какое-то решение 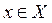 ? В частности, чему будет равен, при данном решении х, выбранный показатель эффективности Z. Для решения такой задачи строится математическая модель, позволяющая выразить один или несколько показателей эффективности через заданные условия и элементы решения.
? В частности, чему будет равен, при данном решении х, выбранный показатель эффективности Z. Для решения такой задачи строится математическая модель, позволяющая выразить один или несколько показателей эффективности через заданные условия и элементы решения.
Обратные задачи отвечают на вопрос: как выбрать решение х для того чтобы показатель эффективности Z обратился в максимум.
Естественно, прямые задачи проще обратных. Очевидно также, что для решения обратной задачи, прежде всего надо уметь решать прямую.
По фактору времени модель может быть отнесена к двум классам: статические и динамические. Если речь идет о моментном описании, то модель относится к классу статики, а если необходимо учесть развитие ситуации во времени, то модель будет динамической.
Другим фактором, по которому проводится классификация модели, является фактор неопределенности.
Классификация по этим двум факторам приведена на схеме рис. 2.
| Модели | |
| Статика | Динамика |
| 1. Определенность | |
| - Линейное программирование - Нелинейное программирование - Целочисленное программирование - Параметрическое программирование | - Динамическое программирование - Сетевое планирование - Вариационное исчисление |
| 2. Риск | |
| - Стохастическое программирование - Антагонистические игры | - Массовое обслуживание - Стохастическое программирование |
| 3. Неопределенность | |
| 3.1. Нескольких лиц | |
| Теория игр | - Теория позиционных игр - Игры на случайных процессах |
| 3.2. Незнание | |
| - Статистические решения - Игры с природой | - Статистические решения |
| 3.3. Несколько критериев | |
| - Многоцелевая оптимизация - Групповые решения - Игры с природой | - Многоцелевая оптимизация в функциональных пространствах |
Рис. 2
Неопределенность возникает тогда, когда не все параметры модели находятся под контролем лица принимающего решение. Это приводит к тому, что при оценке ситуации, последствия действий, которые мы можем предпринять, не известны в точности из-за того, что они зависят еще и от некоторых событий, которые мы не можем контролировать или предвидеть, а их исходы неизбежно отразятся на результате наших действий. Очевидно, что подобная неопределенность возникает во многих практических ситуациях, где необходимо принять решение не сиюминутной важности.
При классификации по фактору наличия неопределенности следует учитывать характер связи между альтернативами (вариантами) и исходами (результатами). При этом возникают три возможности: модель может не содержать неопределенности, может содержать неопределенности в форме риска, и может быть отнесена к классу «неопределенность».
Отнесение к тому или иному классу задач принятия решений в значительной степени носит субъективный характер. Чем удачнее будет подобрана математическая модель, чем лучше она будет отражать характерные черты явления, тем успешнее будет исследование и полезнее – вытекающие из него рекомендации.
МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ
В задачах линейного программирования рассматривались только самые простые случаи, когда был ясен критерий, по которому производилась оценка эффективности, и требовалось обратить в максимум (минимум) один – единственный показатель. К сожалению, на практике такие задачи, где критерий оценки однозначно диктуется целевой направленностью операции, встречается не так уж часто – преимущественно при рассмотрении небольших по масштабу и скромных по значению мероприятий. А когда речь идет о крупномасштабных, сложных операциях, затрагивающих разнообразные интересы их организаторов и общества в целом, то их эффективность, как правило, не может быть полностью охарактеризована с помощью одного – единственного показателя эффективности. На помощь ему приходится привлекать другие, дополнительные. Такие задачи принятия решений называются многокритериальные.
Рассмотрим задачу принятия решений (ЗПР) в условиях неопределенности (т.е. когда каждой альтернативе соответствует множество исходов). В этой задаче исходы оцениваются по двум показателям, а цель состоит в увеличении их обоих.
Эти показатели описываются функциями 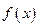 и
и 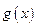 , которые являются оценками исходов.
, которые являются оценками исходов.
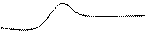
Рассмотрим два примера на рис. 3
Функция Функция
 |  |





 1 2
1 2


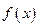
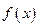
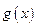
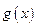
А В х С х
Рис. 3
Во 2-ом примере очевидно, что наилучший исход – в точке С (обе функции достигают максимального значения).
В 1-ом примере (более общий случай) возникает вопрос, что следует понимать под оптимальным решением (точку А или В).
Определение: ЗПР в условиях неопределенности, которая вызвана наличием нескольких критериев, оценки исхода у лица, принимающего решение (ЛПР) называется многокритериальной задачей.
Рассмотрим пример такой задачи.
Организуется (или реорганизуется) работа промышленного предприятия. Под углом зрения какого критерия надо выбирать решение? С одной стороны, нам хотелось бы обратить в максимум валовой объем продукции V. Желательно так же было бы получить максимальный доход D. Что касается себестоимости S, то ее хотелось бы обратить в минимум, а производительность труда П – в максимум. При обдумывании задачи может возникнуть еще ряд дополнительных критериев.
Такая множественность показателей эффективности, из которых одни желательно обратить в максимум, а другие – в минимум, характерна для любой сколько-нибудь сложной задачи принятия решений.
Пример. Конструкторская фирма получила заказ на разработку новой модели автомобиля. Заказчика интересуют два показателя:
U – срок службы,
V – максимальная скорость.
Заказчик желает максимизировать и срок службы, и скорость.
В процессе разработки можно варьировать некоторые технические характеристики автомобиля, такие как, объем двигателя, количество клапанов и т.п. Эти технические характеристики назовем управляемыми, (т.е. их можно изменять). Каждому фиксированному набору значений управляемых характеристик соответствует определенное значение пары 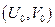 . Если в подобного рода задачах речь идет не о разнородных критериях некоторой системы, а о сопоставлении однородных критериев разных ее подсистем (например, отрасли, группы населения или, как в нашей задаче, технические характеристики различных частей двигателя автомобиля), то такие задачи называются задачами векторной оптимизации.
. Если в подобного рода задачах речь идет не о разнородных критериях некоторой системы, а о сопоставлении однородных критериев разных ее подсистем (например, отрасли, группы населения или, как в нашей задаче, технические характеристики различных частей двигателя автомобиля), то такие задачи называются задачами векторной оптимизации.
В качестве альтернативы выступает набор управляемых параметров, а в качестве исхода рассматривается числовой вектор, координатами которого являются значения интересующих нас показателей. Таким образом, альтернативы – это различные технические характеристики, а исходы – это вектор с координатами 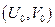 .
.
Связь между ними в этом случае – функциональная, тогда получаем ЗПР в условиях определенности.
ОПТИМАЛЬНОСТЬ ПО ПАРЕТО
Это понятие является одним из важнейших во всей экономической теории. Вместе с тем в нем нет ничего, кроме здравого смысла.
Продолжаем рассматривать многокритериальную задачу. Представим себе, что какой-то вариант решения имеет преимущество над другими по всем показателям; ясно, что именно его следует предпочесть. Но гораздо чаще встречаются случаи, когда с первого взгляда ситуация неясна: один из показателей тянет в одну сторону, другой – в другую. Для выбора решения необходимо «выбраковать» из множества возможных решений заведомо неудачные, уступающие другим по всем критериям. Пусть в составе множества возможных решений есть два решения такие, что все критерии для первого решения больше или равны соответствующим критериям для второго решения, причем хотя бы один из них действительно больше. Очевидно, тогда в составе множества возможных решений нет смысла сохранять второе решение, оно вытесняется (или «доминируется») первым решением. Отбросим второе решение как неконкурентоспособное и перейдем к сравнению других по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество обычно сильно уменьшается: в нем сохраняются так называемые эффективные (иначе «паретовские») решения, характерные тем, что ни для одного из них не существует доминирующего решения.
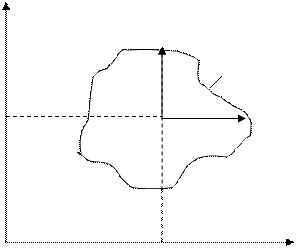
Вернемся к задаче, описанной в предыдущем примере, и рассмотрим ее геометрическое представление (рис. 4).
V
A
D
 V0 M 0 B
V0 M 0 B
U 0 U
Рис. 4
Каждый исход представим как точку в системе координат с осями U, V. Множество этих точек образует некоторую область D, которая и представляет собой область возможных исходов. Нам необходимо найти решение, которое максимизирует оба показателя и U и V.
Геометрически наша задача сводится к задаче выбора точки из множества D.
Возьмем точку М 0 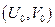 . Построим криволинейный треугольник АМ 0 В, проведя из т. М 0 прямые параллельные осям координат. Для каждой точки этого треугольника значения обоих показателей больше чем U 0 и V 0. Это означает, что выбор любой точки этого треугольника более целесообразен, чем выбор самой точки М 0 т.е. точка М 0 не является оптимальным решением.
. Построим криволинейный треугольник АМ 0 В, проведя из т. М 0 прямые параллельные осям координат. Для каждой точки этого треугольника значения обоих показателей больше чем U 0 и V 0. Это означает, что выбор любой точки этого треугольника более целесообразен, чем выбор самой точки М 0 т.е. точка М 0 не является оптимальным решением.
Такие же рассуждения можно применить к любой точке множества D, для которой возможно построение треугольника АМ 0 В. Следовательно, при выборе оптимального исхода необходимо ограничиваться теми точками множества D, для которых построение подобных треугольников невозможно. Таким образом, из всего множества D эффективными будут только решения, лежащие на правой верхней границе области возможных решений (т.е. в северо-восточной части множества D). Для всякого другого решения существует хотя бы одно доминирующее, для которого либо U, либо V, либо оба показателя больше, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих не существует.
Определение. Исходы, для которых невозможно одновременное улучшение обоих показателей, называется эффективными (или оптимальными) по Парето.
Итальянский экономист Парето в первой половине ХХ века математически сформулировал один из самых распространенных критериев оптимальности для проверки следующего предположения: улучшает ли предложенное изменение в экономике общий уровень благосостояния?
Критерий Парето формулируется так: «Следует считать, что любое изменение, которое никому не причиняет убытков и которое некоторым приносит пользу, является улучшением».
Условие эффективности по Парето звучит так: Точка с координатами (U; V) из области D эффективна, если для любой точки 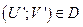 , такой, что
, такой, что 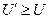 и
и 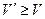 выполняется условие
выполняется условие 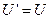 и
и 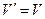 , т.е. точка
, т.е. точка 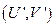 совпадает с точкой (U, V), следовательно, выбор исхода следует производить из множества эффективных точек.
совпадает с точкой (U, V), следовательно, выбор исхода следует производить из множества эффективных точек.
Отсюда следует и другое: принимаемое решение не может быть улучшено в интересах ни одного из партнеров, если оно ухудшает положение хотя бы одного из других.
Такое решение и отвечает оптимуму по Парето, потому, что в данных условиях лучшего получить не представляется возможным.
Однако какую именно эффективную точку следует признать оптимальной?
Сравним две эффективные точки 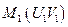 и
и  , представленные на рис. 5
, представленные на рис. 5
V
 M 2
M 2


 V2
V2

 V1 M1
V1 M1
 |
U2 U1 U
Рис. 5
Из рисунка видно, что 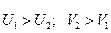 - для точки
- для точки 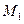 больше срок службы, а для
больше срок службы, а для  - скорость.
- скорость.
Для эффективных точек такая ситуация является типичной. Из определения ясно, что если для одной из точек области  оба показателя являются большими, чем для другой (или, по крайней мере, один показатель строго больше), то эта другая точка не будет эффективной.
оба показателя являются большими, чем для другой (или, по крайней мере, один показатель строго больше), то эта другая точка не будет эффективной.
Итак, считая для двух точек области D лучшей ту, для которой все показатели лучше, получаем, что для любых двух эффективных точек ни одна не является лучше другой.
Иначе говоря, эффективные точки являются несравнимыми между собой по предпочтению. Если мы все же хотим сравнивать эффективные точки, то для этого потребуется дополнительная информация. Чаще всего речь идет о том, чем именно может «пожертвовать» ЛПР ради того, чтобы получить единственное решение, а не множество эффективных точек. Точнее, нужно знать: сколькими единицами выигрыша по одному показателю можно компенсировать проигрыш единицы по другому показателю.
Аналогично строится множество эффективных решений и в случае, когда показателей не два, а больше (при их числе больше трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется).
Вывод: Одним из методов решения многокритериальных задач принятия решений является выбор оптимума по Парето (нахождение множества эффективных точек).
Для построения множества эффективных точек в каждой конкретной ЗПР используется так называемые «процедуры принятия решений». Они выполняются с применением численных методов и основаны на принципе отсечения ненужных исходов из всего множества возможных исходов.
Оставшееся в результате такого отсечения множества эффективных точек и есть решение ЗПР. Это множество называется кривая Эджворта. Каждая из множества этих точек не хуже другой, при этом выбрать какую-то одну из них в качестве решения можно только при наличии дополнительной информации, предоставленной ЛПР. Средствами математики выбрать единственное решение невозможно.
Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. Только человек, с его непревзойденным умением решать неформальные задачи, принимать так называемые «компромиссные решения» (не строго оптимальные, но приемлемые по ряду критериев) может взять на себя ответственность за окончательный выбор.
Таким образом, для многокритериальных задач, как правило, не существует исхода наилучшего по всем показателям одновременно, поэтому для таких задач оптимальное решение называют компромиссным.
МЕТОДЫ НАХОЖДЕНИЯ КОМПРОМИССНОГО РЕШЕНИЯ
Поиск компромиссного решения осуществляется различными методами в зависимости от вида дополнительной информации.
Метод 1.
Каждому показателю, который оптимизируется, приписывается коэффициент важности или удельный вес. Например, в рассмотренной ранее задаче срок службы автомобиля (U) в 1,5 раза важнее для заказчика, чем его скорость (V) (в данном случае 1,5 означает отношение 3:2).
При таком подходе критерии «взвешиваются» по важности и им приписывается некий вес.
Записываем соотношение: 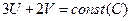 , где С – важность.
, где С – важность.
Выберем 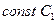 . Построим прямую
. Построим прямую 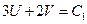 .
.
Будем двигать эту прямую вправо и вверх параллельно самой себе, пока не дойдем до северо-восточной части границы множества D. Точка пересечения этой прямой с границей множества D, и будет оптимальной (U *, V *).
 V
V 


 V*
V*
 |
|
D
 U*
U*
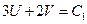 U
U
Рис. 6
Метод 2. «свертки критериев».
Пусть имеется набор критериев 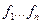 . С помощью дополнительной информации строится один собирательный критерий f (т.е. проводим процесс «свертки»), и далее решается задача для этого критерия.
. С помощью дополнительной информации строится один собирательный критерий f (т.е. проводим процесс «свертки»), и далее решается задача для этого критерия.
Фирме требуется выбрать оптимальную стратегию по обеспечению нового производства оборудованием. С помощью экспериментальных наблюдений были определены значения различных критериев функционирования соответствующего оборудования, которое выпускается тремя заводами-изготовителями. Соответствующие критерии приведены в таблице.
Таблица
| Варианты оборудования (Альтернативы или решения) | Частные критерии эффективности оборудования | |||
| Производитель-ность (Денежные единицы) | Стоимость оборудования (Денежные единицы) | Энергоем-кость (Условные единицы) | Надежность (Условные единицы) | |
| 1. Оборудование завода 1 (решение или альтернатива X 1) | 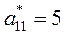
| 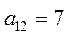
| 
| 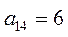
|
| 2. Оборудование завода 2 (X 2) | 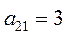
| 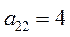
| 
| 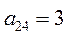
|
| 3. Оборудование завода 3 (Х 3) | 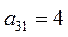
| 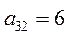
| 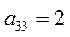
| 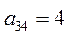
|
Примечание: * 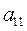 - критерий 1 для оборудования завода 1.
- критерий 1 для оборудования завода 1.
На основе экспертных оценок были определены веса каждого из критериев. Вес обозначим 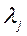 (еще его можно назвать уровень значимости или важность)
(еще его можно назвать уровень значимости или важность)
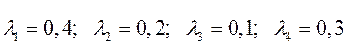
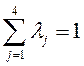
Так, например 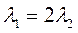 , следовательно, производительность для фирмы в 2 раза важнее.
, следовательно, производительность для фирмы в 2 раза важнее.
Если бы перед нами стояла задача выбора оборудования только по одному критерию, то проблемы бы не возникло. Например, если бы мы выбирали по производительности, то выбрали бы завод 1.
Но выбор оптимального решения по нескольким критериям является многокритериальной задачей.
На данном примере и рассмотрим метод «сверки критериев», который еще называют методом аддитивной оптимизации.
Найдем функцию
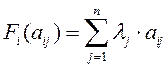 , где
, где 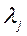 - важность критерия
- важность критерия
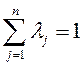
Для начала рассмотрим упрощенный вариант нашей задачи, а именно, будем считать, что в нашем распоряжении есть только два однородных критерия, т.е. критерии, имеющие одинаковую размерность. Выберем производительность и стоимость.
Теперь будем решать двухкритериальную задачу.
Пусть 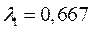 и
и 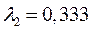 .
.
Рассчитаем значения 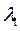 и
и 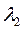 из системы уравнений
из системы уравнений
|
|
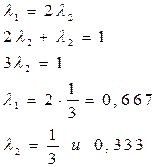
Найдем значения аддитивных функций для упрощенного примера.
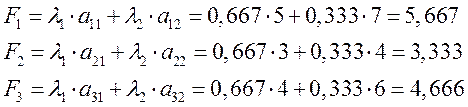
Из полученных значений аддитивных функций, выбираем максимальное 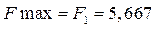 , следовательно, первый вариант оборудования является предпочтительным по двум первым критериям.
, следовательно, первый вариант оборудования является предпочтительным по двум первым критериям.
Эту же задачу можно решать по энергоемкости и надежности.
Пусть 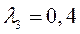 и
и 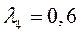
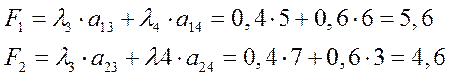
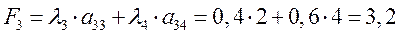
Вывод: по энергоемкости и надежности также предпочтительным является оборудование завода 1.
Если же все критерии имеют разную размерность. То пред решением необходимо провести процедуру нормализации критериев, т.е. привести критерии к безразмерному виду.
Нормализация – процесс пересчета критериев.
Для этого определим max и min по каждому критерию (максимальное и минимальное в каждом столбце):

Затем по экономическому смыслу выделим группу критериев, которые максимизируются, и пронумеруем их 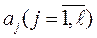 , и группу критериев которые минимизируются
, и группу критериев которые минимизируются 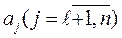 .
.
Критерии производительность и надежность попадут в первую группу, а во вторую стоимость и энергоемкость.
Значения нормализованных критериев определяются из следующих соотношений:
 , для
, для 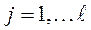 (для критериев, которые максимизируются)
(для критериев, которые максимизируются)
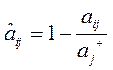 , для
, для 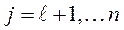 (для критериев, которые
(для критериев, которые
минимизируются)
Оптимальным будет тот вариант, который обеспечит максимальное значение аддитивной функции
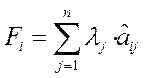
1. Найдем 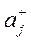
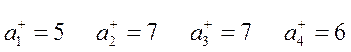
2. Найдем 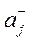
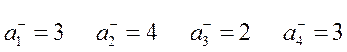
3. Максимизируются два критерия: производительность 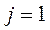 и надежность
и надежность 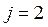 , следовательно,
, следовательно, 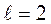 .
.
Тогда критерии, которые минимализируются имеют номера 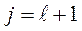 , и это – стоимость
, и это – стоимость 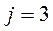 и надежность
и надежность 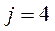 .
.
Находим нормализованные критерии:
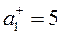
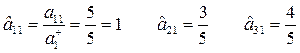
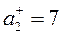
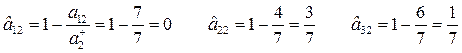
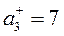
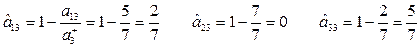
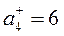
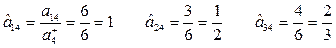
Затем найдем аддитивные функции
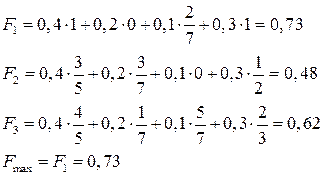
Вывод: необходимо приобрести оборудование завода 1.
Метод 3. метод уступок решения задач многокритериальной оптимизации
Пусть в задаче многокритериальной оптимизации есть несколько критериев
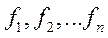
В таких задачах критерий – это синоним целевой функции.
Расположим их по значимости, причем самый важный будет иметь номер 1 и т.д.
I этап: Решаем задачу по первому критерию на области допустимых решений (ОДР) D, при этом получим оптимальное значение первого критерия f 1.
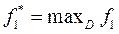
II этап: Делаем «уступку» по первому критерию, т.е. уменьшаем величину 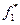 до значения
до значения 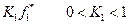 , где К 1 – уступка по первому критерию.
, где К 1 – уступка по первому критерию.
III этап: Вводим в задачу дополнительное ограничение
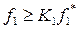 (*)
(*)
IV этап: Решаем задачу по второму критерию с новой системой ограничений, а именно, к ОДР добавляется еще одно условие:
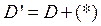 , т.е.
, т.е. 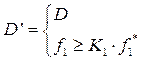
скорее всего, ОДР сузится, и т.д. последовательно по всем критериям.
В результате решения по второму критерию получим

Будем действовать так последовательно по всем критериям.
Процесс заканчивается, когда будет получено решение по всем критериям. Окончательный план и будет эффективным. При этом получим экстремальное значение критерия наименьшей важности (fm) при условии гарантированных значений предшествующих критериев.
Пример 1. Решение с помощью графического метода.
Рассмотрим задачу о выпуске продуктов двух видов, при условии максимизации прибыли и минимизации затрат на хранение в условиях ограниченности ресурсов
 (прибыль)
(прибыль)
 (затраты на хранение)
(затраты на хранение)
Область допустимых значений
D 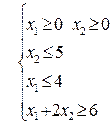 ,
,
где x 1 и x 2 - количество выпускаемой продукции первого и второго вида.
Уступка по первому критерию 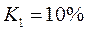 , что означает, что можно уменьшить
, что означает, что можно уменьшить 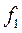 на 10%, т.е. оставить 90% или 0,9.
на 10%, т.е. оставить 90% или 0,9.
Самым важным критерием будет прибыль, следовательно, начинаем решать задачу по первому критерию на область D.

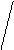
|

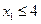
 | |||
| |||
|


|
|
|
|
|


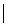
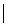
Рис. 7
1) Построим прямую
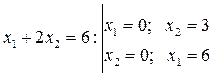
2) И еще две прямые 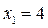 и
и 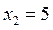
3) Затем определяем положение ОДР. Например, для прямой 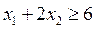 , подставляем точку с координатами
, подставляем точку с координатами 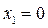 и
и  в формулу неравенства, и получаем
в формулу неравенства, и получаем 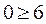 . Это неравенство неверно, следовательно, ОДР будет направлена от точки (0;0), ставим стрелку в сторону от нуля.
. Это неравенство неверно, следовательно, ОДР будет направлена от точки (0;0), ставим стрелку в сторону от нуля.
4) Определяем координаты конца вектора нормали из критерия 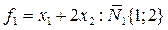 , и строим этот вектор.
, и строим этот вектор.
5) Перпендикулярно вектору нормали строим линию уровня 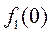 . Двигаем линию уровня параллельно самой себе в направлении вектора нормали
. Двигаем линию уровня параллельно самой себе в направлении вектора нормали  , до тех пор пока линия уровня не станет опорной к ОДР (т.е. не будет касаться ее в одной точке) и находим
, до тех пор пока линия уровня не станет опорной к ОДР (т.е. не будет касаться ее в одной точке) и находим 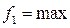 в точке А с координатами
в точке А с координатами 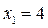 и
и 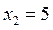 . Отсюда
. Отсюда 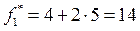 .
.
6) Выводим уступку на 10%.
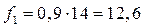 .
.
Теперь решаем задачу с добавлением ограничения в области 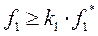 , т.е.
, т.е. 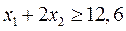 и получаем область
и получаем область 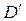
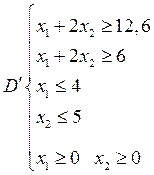
Задачу решаем по векторному критерию
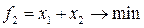
7) Строим область 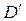 . Добавляем прямую:
. Добавляем прямую:
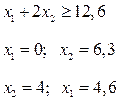
Определяем конец вектора нормали 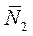 из второго критерия
из второго критерия
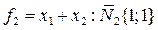
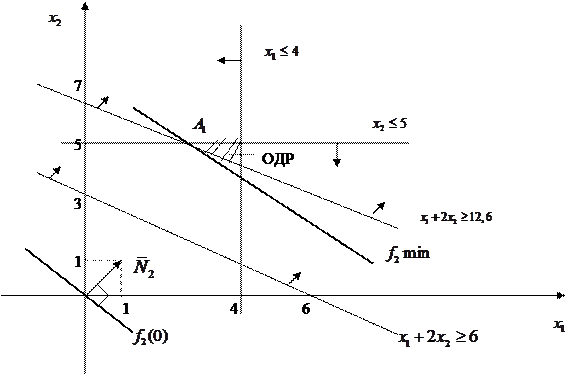 |
Рис. 8
Строим линию уровня 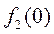 перпендикулярно вектору
перпендикулярно вектору 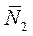 и находим точку А1, которая является точкой пересечения прямых
и находим точку А1, которая является точкой пересечения прямых 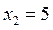 и
и 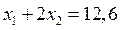 .
.
Отсюда получаем 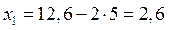 .
.
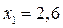 и
и 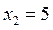 .
.
Тогда 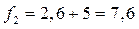
Ответ:
Компромиссным планом будет выпуск 2,6 ед. одного продукта, 5 ед. второго продукта, при этом max прибыли = 12,6, а min затрат = 7,6. Субоптимальные планы (т.е. оптимальные планы на каждом этапе), приводящие к компромиссному решению образуют цепочку (точка А  точка А 1 и т.д.).
точка А 1 и т.д.).
Пример 2. Решение с помощью симплексного метода.
Найдем компромиссное решение следующей задачи:
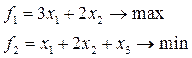
при ограничениях
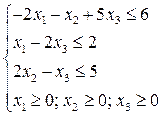
При условии, что уступка по первому критерию составляет 50 %.
Уступка 50 % означает, что можно отклониться от максимального значения первой целевой функции ровно на половину.
Решение:
1. Решаем задачу по первому критерию, т.е. решаем следующую задачу линейного программирования с помощью симплексного метода:
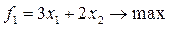
при ограничениях
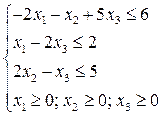
1.1. Приводим задачу к каноническому виду, для этого вводим дополнительные переменные  и
и  .
.
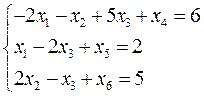
Дополнительные переменные входят в целевую функцию с коэффициентом ноль.
Получаем новую целевую функцию 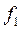 :
:
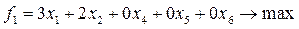
1.2. Составляем первую симплексную таблицу.
Таблица 1
| Базис | 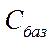
| 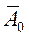
| |||||||
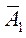
| 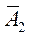
| 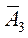
| 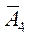
| 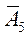
| 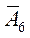
| |||||
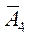
| -2 | -1 | ||||||||
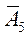
| -2 | |||||||||
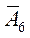
|  0 0
| -1 | ||||||||
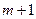
| 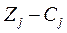
|  -3 -3
| -2 |
1.3. Проверяем план на оптимальность по «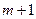 » - ой строке. Для решения задачи на максимум все оценки
» - ой строке. Для решения задачи на максимум все оценки 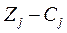 должны быть положительны. Следовательно, этот план не оптимальный.
должны быть положительны. Следовательно, этот план не оптимальный.
1.4. Два вектора 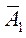 и
и 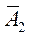 имеют отрицательные оценки. Определяем вектор, который нужно включить в базис – это вектор
имеют отрицательные оценки. Определяем вектор, который нужно включить в базис – это вектор 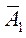 , т.к. его оценка
, т.к. его оценка 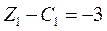 более отрицательна, чем
более отрицательна, чем 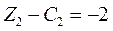 .
.
Затем определяем вектор, который будем исключать из базиса. Для этого определяем величину 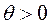 .
.
Дата публикования: 2014-11-02; Прочитано: 405 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!