 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Функции 2 страница
|
|
Рис.1
Число клеток в диаграмме определяется как число двоичных наборов, т.е. 2n, где n - число переменных, от которых зависит функция.
Пример:
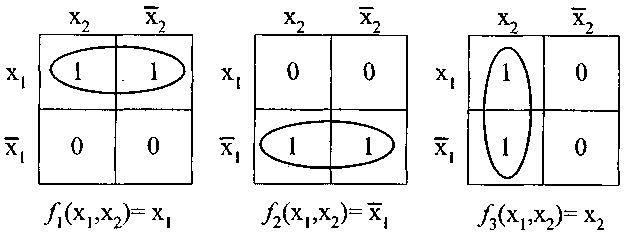
Рис.2 Рис.3 Рис.4
Правильной конфигурацией является прямоугольник
по вертикали или по горизонтали.
Для функции трех переменных диаграмма Вейча
имеет вид, показанный на рис. 5.
Правильными конфигурациями являются прямоугольники по вертикали, по горизонтали и квадраты. Крайние левый и правый столбцы являются соседними. 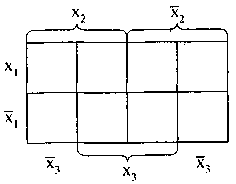
Рис. 5
Если требуется минимизировать булеву функцию
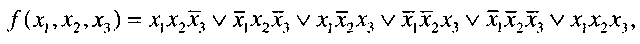
то можно найти два минимальных накрытия единиц таблицы правильными конфигурациями (см. рис. 6, 7),
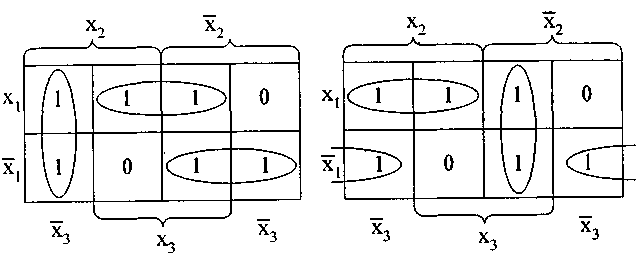
Рис. 6 Рис. 7
которым соответствуют две тупиковые ДНФ, являющиеся минимальными:
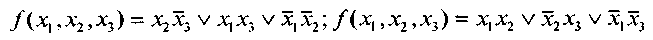
Для функции 4-х переменных диаграмма Вейча показана на рис. 8.
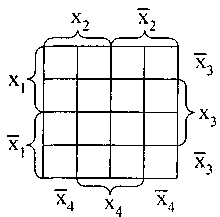 Правильными конфигурациями являются прямоугольники по вертикали, по горизонтали и квадраты. Крайний левый и правый столбцы являются соседними, также как соседними являются верхний и нижний прямоугольники.
Правильными конфигурациями являются прямоугольники по вертикали, по горизонтали и квадраты. Крайний левый и правый столбцы являются соседними, также как соседними являются верхний и нижний прямоугольники.
Рис. 8
Пусть задана булева функция от четырех переменных:
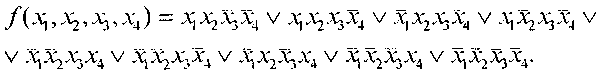
Диаграмма Вейча и минимальное накрытие для неё показаны на рис. 9.
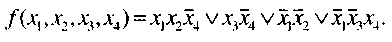
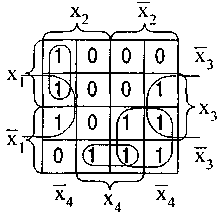 Минимальная ДНФ этой функции имеет вид:
Минимальная ДНФ этой функции имеет вид:
Определим теперь точно понятия правильных конфигураций, и минимальных накрытий.
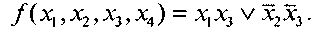 Рис. 9
Рис. 9
Правильными конфигурациями ранга r на диаграмме Вейча для булевой функции от n переменных являются все прямоугольники (вертикальные, горизонтальные и квадратные), имеющие площадь 2n-r (r=l,2,...,n) и только такие прямоугольники.
Совокупность М правильных конфигураций образует накрытие булевой функции 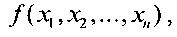 заданной таблицей своих значений, если любое место, в котором значение функции f равно единице, входит хотя бы в одну
заданной таблицей своих значений, если любое место, в котором значение функции f равно единице, входит хотя бы в одну
конфигурацию системы М. Рангом накрытия называется сумма рангов всех образующих накрытие правильных конфигураций.
Накрытие функции называется минимальным, если его ранг не превышает ранга любого другого накрытия этой функции с помощью правильных конфигураций.
Дизъюнкция элементарных конъюнкций, которые образуют любое накрытие М булевой функции 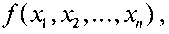 является ДНФ этой функции. ДНФ является минимальной тогда и только тогда, когда накрытие М минимально.
является ДНФ этой функции. ДНФ является минимальной тогда и только тогда, когда накрытие М минимально.
Минимизацию булевых функций с помощью диаграмм Вейча можно осуществлять и в том случае, когда исходная функция задается в ДНФ.
Пусть, например, дана булева функция:
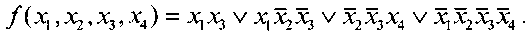
Диаграмма Вейча для нее показана на рис. 10.
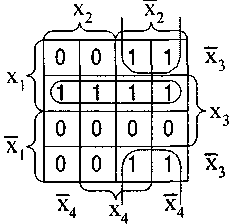 По диаграмме находим минимальное накрытие единиц булевой функции двумя правильными конфигурациями второго ранга. Поэтому минимальная ДНФ исходной функции запишется в виде:
По диаграмме находим минимальное накрытие единиц булевой функции двумя правильными конфигурациями второго ранга. Поэтому минимальная ДНФ исходной функции запишется в виде:
Рис. 10
3.4. Минимизация не полностью определенных (частичных) булевых функций
Если булева функция 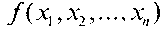 определена не на всех 2nнаборах аргументов, то она называется не полностью определенной или частичной булевой функцией.
определена не на всех 2nнаборах аргументов, то она называется не полностью определенной или частичной булевой функцией.
Рассмотрение частичных булевых функций связано с тем, что в реальных схемах ЭВМ некоторые комбинации входных сигналов никогда не подаются на входы схемы. Такие комбинации входных сигналов (наборов) называются запрещенными. Для запрещенных входных наборов выходные сигналы не определены, т.е. значения функции 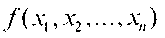 на этих наборах могут быть выбраны произвольно - 0 или 1.
на этих наборах могут быть выбраны произвольно - 0 или 1.
Предположим, что булева функция 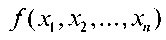 не определена на р входных наборах. Тогда полностью определенную булеву функцию
не определена на р входных наборах. Тогда полностью определенную булеву функцию 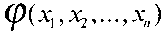 ,называют эквивалентным продолжением булевой функции
,называют эквивалентным продолжением булевой функции 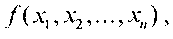 если значения
если значения 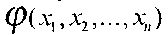 на тех наборах, на которых определена
на тех наборах, на которых определена 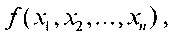 совпадают со значениями функции
совпадают со значениями функции 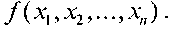
Существует 2Р значений функций на запрещенных наборах и, следовательно, 2Р различных булевых функций 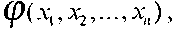 которые являются эквивалентными продолжениями функции
которые являются эквивалентными продолжениями функции 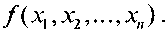 Задача минимизации частичной булевой функции
Задача минимизации частичной булевой функции 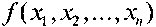 сводится к отысканию такой функции
сводится к отысканию такой функции 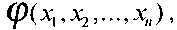 которая имеет простейшую минимальную форму, т.е. форму, имеющую наименьший ранг.
которая имеет простейшую минимальную форму, т.е. форму, имеющую наименьший ранг.
Минимизацию частичных булевых функций будем выполнять с помощью диаграмм Вейча, причем в клетках
диаграммы, которые соответствуют запрещенным наборам, будем ставить «-» (прочерк).
Пусть булева функция 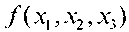 задана в виде таблицы истинности (см. табл. 5).
задана в виде таблицы истинности (см. табл. 5).
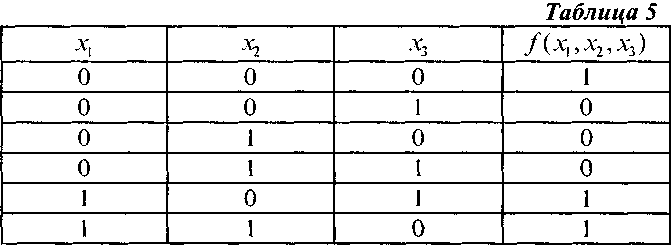
Тогда диаграмма Вейча этой функции будет иметь вид, показанный на рис. 11.
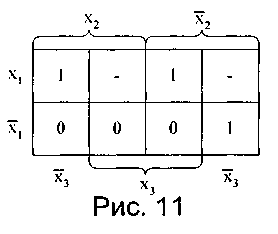
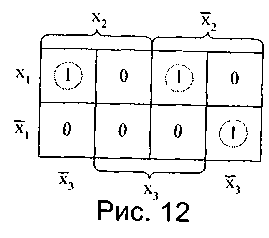
Если исходную функцию доопределить нулями (см. рис. 12), то минимальная ДНФ будет иметь вид:
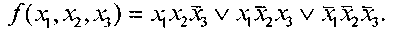
Если исходную функцию доопределить единицами (см. рис. 13), то минимальная ДНФ имеет вид:
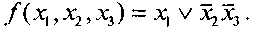
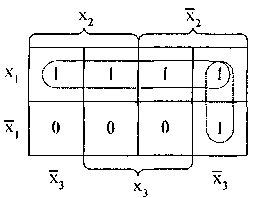
Рис. 13
В дальнейшем для упрощения будем строить правильные конфигурации на диаграмме Вейча из единиц, нулей и прочерков. Причем, если прочерк охватывается правильной конфигурацией, то это означает, что функция доопределяется единицей. Если прочерк не охватывается правильной конфигурацией, то функция доопределяется нулем.
Пример 1. Задана булева функция f (x1, x2, х3) в виде диаграммы Вейча (см. рис.14). Определяем для нее минимальное накрытие и записываем минимальную ДНФ:
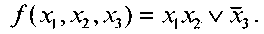
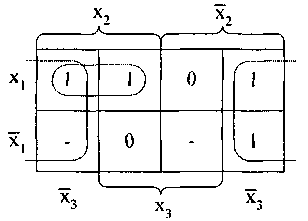
Рис. 14
Пример 2. Задана булева функция 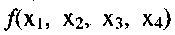 в виде диаграммы Вейча (см. рис.15). Определяем для нее минимальное накрытие и записываем минимальную ДНФ:
в виде диаграммы Вейча (см. рис.15). Определяем для нее минимальное накрытие и записываем минимальную ДНФ:
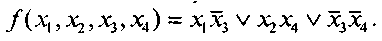
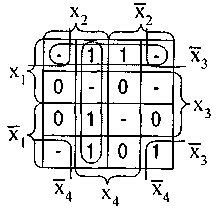
Рис. 15
Контрольные вопросы
1. Какая конъюнкция называется элементарной?
2. Что называют рангом элементарной конъюнкции?
3. Какая дизъюнктивная нормальная форма (ДНФ) и какая конъюнктивная нормальная форма (КНФ) называются минимальными?
4. С помощью каких операций (преобразований) достигается упрощение совершенной дизъюнктивной нормальной формы?
5. Назовите основные этапы алгоритма минимизации по методу Квайна-Мак-Класки.
6. Каково исходное задание булевой функции при минимизации по методу Квайна-Мак-Класки?
7. Покажите, как строится импликантная таблица.
8. В чем состоит основная идея минимизации булевых функций методом диаграмм Вейча?
9. Определите понятия правильных конфигураций, накрытий и минимальных накрытий.
10. Каковы особенности минимизации частичных булевых функций?
4. КОМБИНАЦИОННЫЕ СХЕМЫ И КОНЕЧНЫЕ
АВТОМАТЫ
4.1. Понятие комбинационной схемы
Комбинационная схема - это схема, работающая в дискретном времени, причём сигналы на выходе схемы в данный момент времени однозначно определяются сигналами на её входе и не зависят от сигналов, поданных в предыдущие моменты времени. Комбинационные схемы (КС) называют иногда автоматами без памяти и представляют в виде (n,m)-полюсника (см. рис. 16),
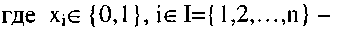
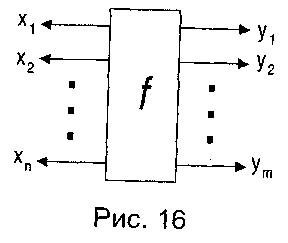 двоичные или булевы переменные;
двоичные или булевы переменные;
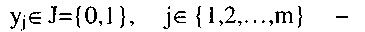 функции алгебры логики или булевых функций:
функции алгебры логики или булевых функций: 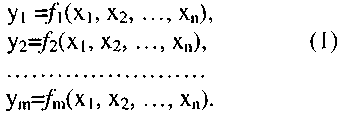
Совокупность m булевых функций от n переменных описывает любую комбинационную схему или (n,m)-полюсник.
Введём обозначения:
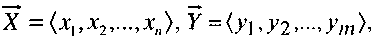

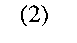
где 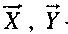 - соответственно входная и выходная векторные переменные, f - оператор, реализуемый комбинационной схемой.
- соответственно входная и выходная векторные переменные, f - оператор, реализуемый комбинационной схемой.
4.2. Задачи анализа и синтеза КС
Задача анализа комбинационных схем состоит в том, чтобы по заданной комбинационной схеме определить оператор f (2) или систему булевых функций (1), описывающих работу данной комбинационной схемы.
Задача синтеза комбинационной схемы заключается в том, чтобы по заданному оператору или системе булевых функций построить КС, которая реализует данный оператор или систему булевых функций.
Пусть в нашем распоряжении имеется следующий набор логических элементов:
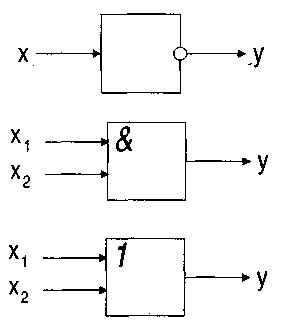
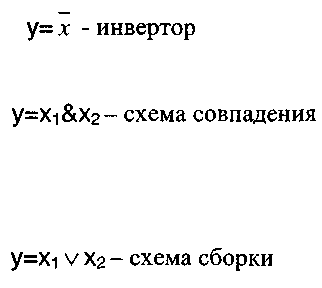
Этот набор является функционально полным набором логических элементов. Поэтому из них можно построить любую комбинационную схему. Пусть задана комбинационная схема (см. рис. 17).
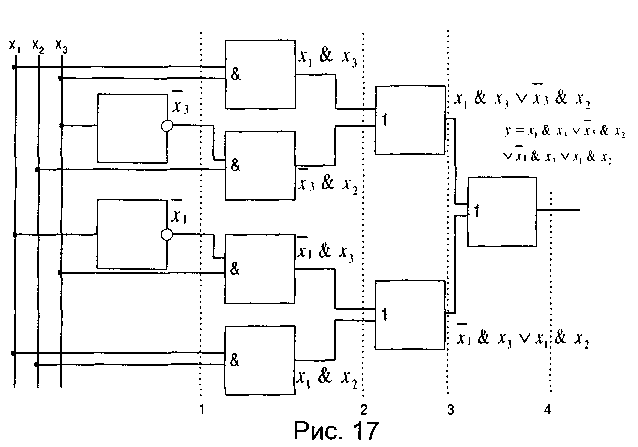
Алгоритм анализа КС можно представить в следующем виде. Пусть предложенная схема разбита на ярусы и в каждом ярусе стоят один или несколько логических элементов. Число ярусов конечно. Проводим секущие плоскости по выходам каждого из ярусов элементов, от первого до последнего. Записываем выходные функции 1-го яруса на основании входных переменных и функций, реализуемых элементами 1-го яруса. Получаем входные функции 2-го яруса. Далее поступаем аналогично для каждого последующего яруса, пока не дойдём до последнего, выход которого и определяет функцию, реализуемую схемой.
Задача синтеза КС состоит из следующих этапов:
1. Формулировка исходного задания на естественном языке.
2. Переход от словесной формулировки к таблице истинности, задающей логическую функцию.
3. Запись формулы логической функции через операции 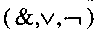 по полученной таблице истинности.
по полученной таблице истинности.
4. Если необходимо, упрощение логической формулы.
5. Составление КС по исходной или упрощённой логической формуле.
Пример 1 Построить комбинационную схему, реализующую следующую логическую функцию: сигнал на выходе появляется, если есть сигнал на любом одном входе или на всех трёх входах сразу.
Это первый этап синтеза КС.
Второй этап. По словесной формулировке записываем таблицу истинности (см. табл. 6).
Таблица 6
| X1 | X2 | X3 | f1 |
Третий этап. Записываем формулу логической функции:
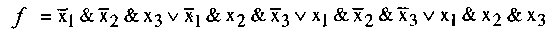 (3)
(3)
Четвёртый этап. Этап упрощения формулы отсутствует, как следует из рис. 18.
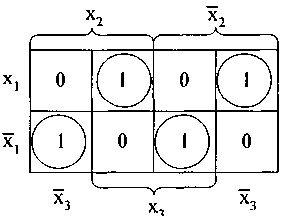
Рис. 18
Пятый этап. Используя ярусную систему (см. рис. 19), по формуле (3) строим КС, которая имеет вид, показанный на рис. 20. Сущность ярусной системы заключается в том, что если на вход схемы подаётся три и более сигналов, то схема сборки или совпадения разбивается с учётом 2-х входовых схем следующим образом:
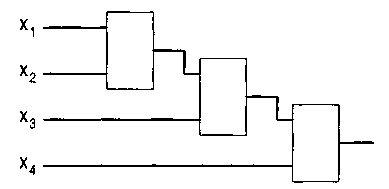
Рис 19
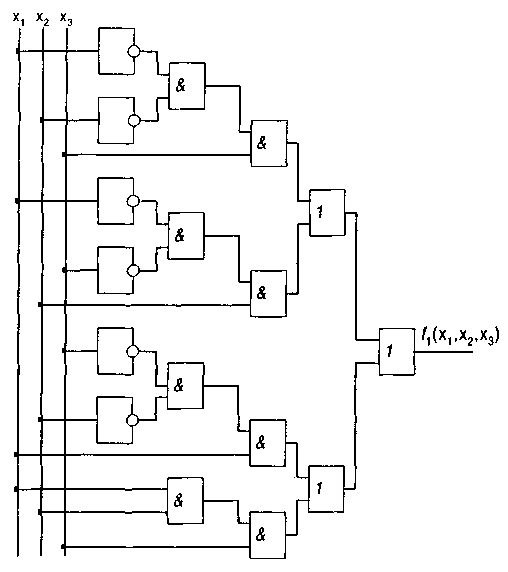
Рис. 20
Полученная схема имеет 17 элементов. Она осуществляет суммирование двух двоичных чисел Х1 и x2, поступающих последовательно разряд за разрядом на её входы с учётом переноса х3из предыдущего (младшего) разряда.
Пример 2. Построить комбинационную схему, реализующую следующую функцию: сигнал на выходе появляется, если есть сигнал на любых двух входах или на всех трёх входах.
Это первый этап синтеза КС
Второй этап. Строим таблицу истинности (см. табл. 7)
Таблица 7
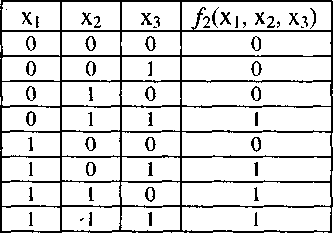
Третий этап. Записываем логическую формулу:
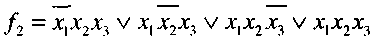 (4)
(4)
Четвертый этап. Упрощаем (минимизируем) логическую формулу (4), в результате получаем:
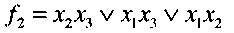 (5)
(5)
Строим комбинационную схему:
а) для исходной функции (4) (см. рис. 21)
б) по упрощенной формуле (5) (см. рис. 22)
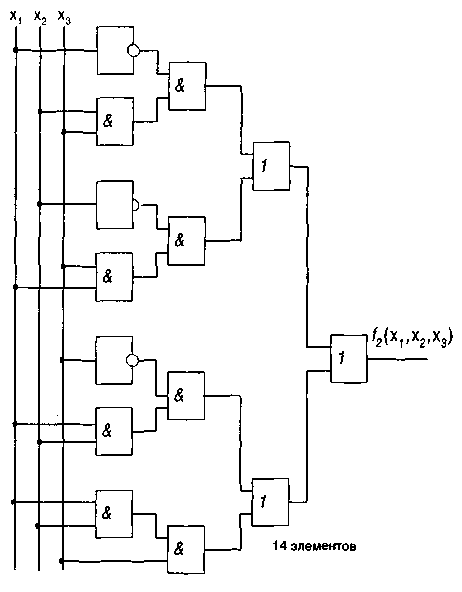
Рис. 21
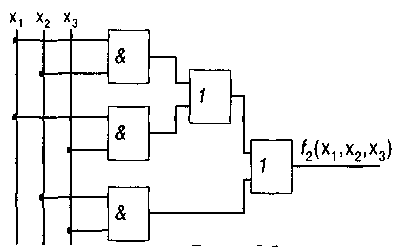
Рис.22
4.3. Понятие цифрового автомата
Цифровым автоматом с памятью называется преобразователь дискретной информации, который может под воздействием входных сигналов переходить из одного состояния в другое, сохранять принятые состояния в период между входными сигналами и выдавать выходные сигналы. Алгоритм переработки информации цифровым автоматом обеспечивается определённой организацией его структуры.
Теория проектирования автоматов разбивается на две части: абстрактную и структурную теорию автоматов.
Абстрактная теория отвлекается от структуры автомата, рассматривая его (автомат) как «чёрный ящик», и основное внимание уделяет поведенческой стороне функционирования автомата, т. е. изучает лишь алгоритм его работы.
Структурная теория занимается нахождением общих приёмов построения схемы цифрового автомата по алгоритму его работы.
4.4. Определение и способы задания абстрактных автоматов
Представим устройство с одним входом и одним выходом, работающее в дискретном времени (см. рис. 23).
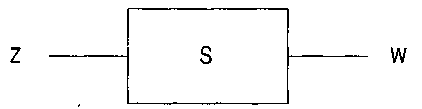
Рис. 23
Предположим, что в дискретные моменты времени t = 0, 1, 2,... на вход устройства поступает входной сигнал
- одна из букв входного алфавита Z, а на его выходе появляется выходной сигнал - буква выходного алфавита W. Под алфавитом здесь будем понимать непустое множество попарно различных символов. Элементы алфавита называются буквами, а конечная упорядоченная последовательность букв - словом в данном алфавите. Зададим входной и выходной алфавиты:
Z = {z1, z2, z3}, W = {w1, w2, w3, w4, w5}.
Пусть на вход устройства поступила последовательность букв (входное слово): z1, z2, z2, z3, z1, z1, z3, в ответ на которую на выходе появилась последовательность букв (выходное слово): w1|, w5, w4, w1 w3, w2, w5 (см. табл. 8).
Таблица 8
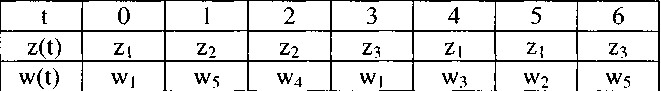
Как следует из табл. 8, реакция устройства на одну и ту же входную букву может быть различной. Например, в моменты времени to, t4, t5- Таким образом, сигнал на выходе устройства в каждый момент времени t зависит не только от входного сигнала в этот же момент t, но и от предшествующего состояния, т. е. в устройстве должна быть память о том, какое слово поступило на его вход до рассматриваемого момента времени. Математической моделью подобных устройств является абстрактный автомат. Термин «абстрактный» используется здесь в связи с идеализированным дискретным временем, а также потому, что в этой модели абстрагируются от реальной физической природы входных и выходных сигналов, рассматривая их просто как буквы некоторого алфавита.
Абстрактный автомат - это пятикомпонентный вектор S = (A, Z, W, 5, X), у которого:
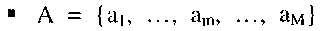 - множество состояний (алфавит состояний), причём a1 -начальное состояние автомата при t = 0;
- множество состояний (алфавит состояний), причём a1 -начальное состояние автомата при t = 0;
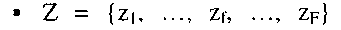 - множество входных сигналов (входной алфавит);
- множество входных сигналов (входной алфавит);
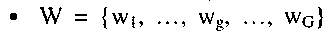 - множество выходных сигналов (выходной алфавит);
- множество выходных сигналов (выходной алфавит);
■ функция переходов δ определяет состояние автомата в следующий момент (t + 1) в зависимости от состояния автомата и входного сигнала в момент времени t, другими словами, функция δ ставит в соответствие паре «состояние - входной сигнал» (am, zf) состояние автомата as, в которое он переходит из аm под действием сигнала zf, т. е. 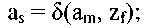
■ функция выходов λ определяет выходной сигнал, который появляется на выходе автомата в момент времени t в зависимости от состояния и входного сигнала в тот же момент времени t. Иначе, функция λ ставит в соответствие паре «состояние - входной сигнал» (am, zf) выходной сигнал 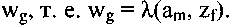
Под работой абстрактного автомата понимается преобразование входных слов в выходные слова.
Наибольшее распространение на практике получили два класса автоматов - автоматы Мили и автоматы Мура.
Функционирование автомата Мили задаётся уравнениями: 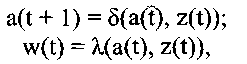
а автомата Мура - уравнениями:
где t = 0, 1, 2,.... 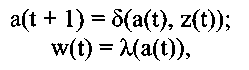
Автомат называется конечным, если конечны множества A, Z, W. Мы будем рассматривать только
конечные автоматы. Автомат называется полностью определённым, если области определения функций δ и λ содержат всевозможные пары вида (аm zf ). У не полностью определённого или частичного автомата функции δ и λ определены не для всех пар «состояние - входной сигнал». Чтобы задать конечный автомат S, необходимо описать все компоненты вектора S = (A, Z, W, δ, λ ), т. е. алфавит состояний, входной и выходной алфавиты, а, также функции переходов и выходов. Кроме того, среди множества состояний необходимо выделить состояние a1, в котором автомат находится в момент времени t = 0. Существует несколько способов задания работы автомата, но наиболее часто используются табличный и графический методы.
При описании работы автомата Мили таблицами переходов (табл. 9) и выходов (табл. 10), строки этих таблиц соответствуют входным сигналам, а столбцы - состояниям, причём крайний левый столбец обозначен начальным состоянием a1. На пересечении столбца аm и строки zf в таблице переходов ставится состояние as = δ (аm, zf), в которое автомат переходит из состояния аm под действием сигнала zf, а в таблице выходов - соответствующий этому переходу выходной сигнал wg = λ (am, zf).
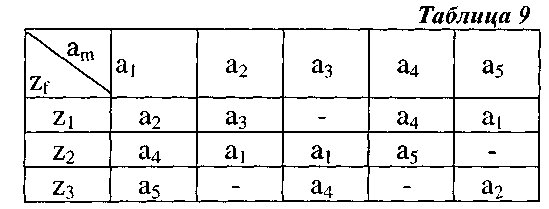
Автомат, 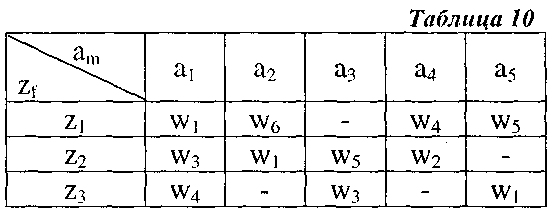 заданный табл. 9 и табл. 10, из состояния а1под действием входного сигнала z2 перейдёт в состояние а4 (см. табл. 9) и выдаст выходной сигнал w3 (см. табл. 10). Рассматриваемый автомат Мили - частичный, на месте неопределённых состояний и выходных сигналов ставится «—».
заданный табл. 9 и табл. 10, из состояния а1под действием входного сигнала z2 перейдёт в состояние а4 (см. табл. 9) и выдаст выходной сигнал w3 (см. табл. 10). Рассматриваемый автомат Мили - частичный, на месте неопределённых состояний и выходных сигналов ставится «—».
Так как в автомате Мура выходной сигнал зависит только от состояния, автомат Мура задаётся одной отмеченной таблицей переходов, в которой каждому её столбцу приписан, кроме состояния аm ещё и выходной сигнал wg = λ (am), соответствующий этому состоянию. Если в автомате Мура функция λ (аm) не определена, то над состоянием аm ставится прочерк «-» (см. табл. 11).
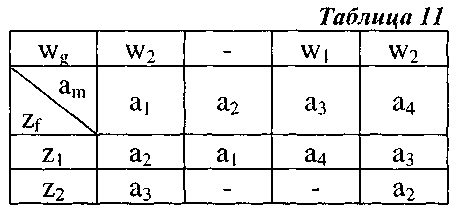
Как следует из табл. 11, автомат, попав, например, в состояние а3, всё время будет выдавать выходной сигнал w1, независимо от того, из какого состояния и под действием какого входного сигнала произошёл переход в а3..
Мы рассмотрели табличный метод задания абстрактных автоматов. Теперь рассмотрим задание автоматов в виде графов.
Граф автомата - ориентированный граф, вершины которого соответствуют состояниям, а дуги - переходам между ними. Две вершины графа автомата 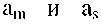 соединяются дугой, направленной от
соединяются дугой, направленной от 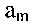 (исходное состояние) к
(исходное состояние) к 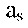 (состояние перехода), если в автомате имеется переход из аm в as при некотором входном сигнале
(состояние перехода), если в автомате имеется переход из аm в as при некотором входном сигнале 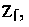 т. е. если
т. е. если 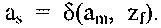 Дуге
Дуге 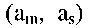 графа автомата приписываются входной сигнал
графа автомата приписываются входной сигнал 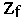 и выходной сигнал
и выходной сигнал 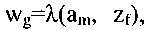 если он определён, и ставится прочерк в противном случае. Если переход автомата из состояния
если он определён, и ставится прочерк в противном случае. Если переход автомата из состояния 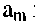 в состояние
в состояние 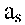 происходит под действием нескольких входных сигналов, то дуге
происходит под действием нескольких входных сигналов, то дуге 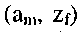 приписываются все эти входные и соответствующие выходные сигналы. При описании автомата Мура в виде графа, выходной сигнал
приписываются все эти входные и соответствующие выходные сигналы. При описании автомата Мура в виде графа, выходной сигнал 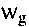
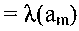 записывается внутри или рядом с вершиной
записывается внутри или рядом с вершиной 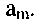
Построим граф автомата Мили, заданного табл. 9 и табл. 10 (см. рис. 24).
Рис.24
Граф автомата Мура, заданный «отмеченной» табл. 11, показан на рис. 25.
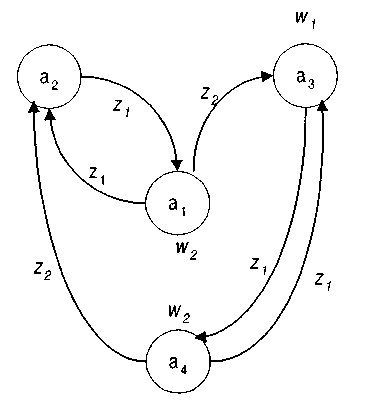
Рис. 25
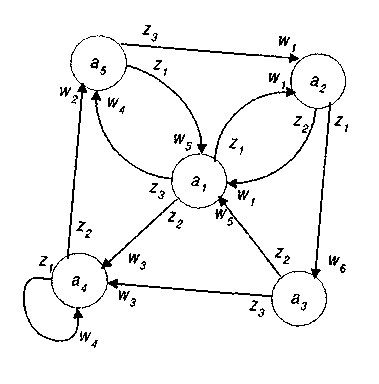
Мы будем рассматривать только детерминированные автоматы. В графе такого автомата из любой вершины не могут выходить две или более дуги, отмеченные одним и тем же входным сигналом. Абстрактный автомат, как отмечалось выше, работает как преобразователь слов входного алфавита в слова в выходном алфавите. Два автомата Sa и Sb с одинаковыми входными и выходными алфавитами называются эквивалентными, если после установления их в начальные состояния их реакции на любое входное слово совпадают.
4.5. Преобразования моделей абстрактных автоматов
Доказано (Глушков В.М. Синтез цифровых автоматов, М, Физматгиз, 1962), что для любого автомата
Мили существует эквивалентный ему автомат Мура, и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили. При трансформации автоматов Мили и Мура будем пренебрегать в автоматах Мура выходным сигналом, связанным с начальным состоянием 
Рассмотрим сначала преобразование автомата Мура в автомат Мили. Пусть задан автомат Мура: 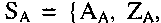
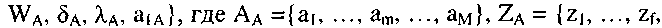
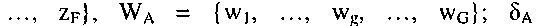 реализует отображение
реализует отображение 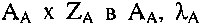 - отображение АA на WA,
- отображение АA на WA, 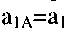 - начальное состояние.
- начальное состояние.
Построим автомат Мили: 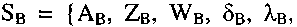
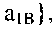 у которого:
у которого: 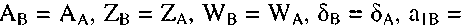
Дата публикования: 2014-11-03; Прочитано: 707 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
