 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Равномерная сходимость функционального ряда
|
|
Среди сходящихся функциональных рядов выделяются своей важностью так называемые равномерно сходящиеся ряды.
Определение 6.2.8. Ряд  (1) называется равномерно сходящимся на множестве Д, если для любого
(1) называется равномерно сходящимся на множестве Д, если для любого 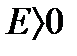 можно указать такое число
можно указать такое число 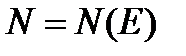 , что при всех
, что при всех  будет выполнятся неравенство:
будет выполнятся неравенство: 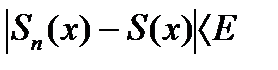 для всех
для всех 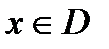 (или
(или 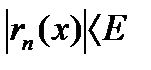 ).
).
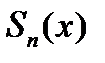 - n-я частичная сумма ряда (1)
- n-я частичная сумма ряда (1)
S(x)- сумма ряда (1)
Рассмотрим следующий признак, достаточный для равномерной сходимости функционального ряда.
Теорема (признак Вейерштрасса) 6.2.15.: Если функциональный ряд  (1) мажорирует на данном множестве Д, то он: 1) равномерно и 2) абсолютно сходится на этом множестве.
(1) мажорирует на данном множестве Д, то он: 1) равномерно и 2) абсолютно сходится на этом множестве.
Пример 6.2.26.Доказать, что ряд 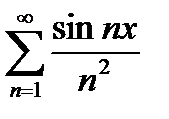 сходится равномерно на всей оси ОХ.
сходится равномерно на всей оси ОХ.
Т. к. для " 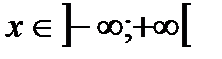 имеем
имеем 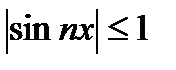 , то
, то 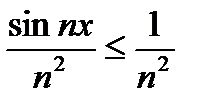 (
( ). Ряд
). Ряд 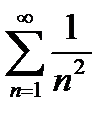 сходится. По признаку Вейерштрасса данный ряд сходится равномерно на всей оси.
сходится. По признаку Вейерштрасса данный ряд сходится равномерно на всей оси.
Замечание 6.2.8.Признак Вейерштрасса дает только достаточное условие равномерной сходимости функционального ряда, оно не является необходимым.
Замечание 6.2.9. Равномерно сходящийся в некотором промежутке ряд не обязательно сходится там и абсолютно.
Дата публикования: 2014-11-03; Прочитано: 619 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
