Пособие по линейному программированию

ПОСОБИЕ ПО ЛИНЕЙНОМУ ПРОГРАММИРОВАНИЮ

Постановка задачи линейного программирования. Основные понятия.

Определение 1. Задача линейного программирования состоит в оптимизации линейной функции, зависящей от конечного числа вещественных переменных, при заданной системе линейных ограничений (имеющих вид равенства или неравенства).

Определение 2. Зависящая от 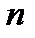переменных 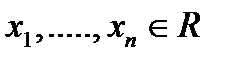функция 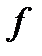называется линейной, если она имеет вид: 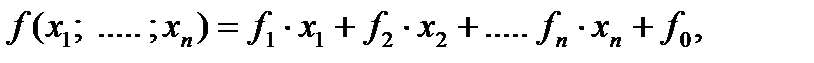где 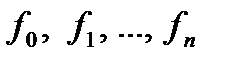- некоторые фиксированные вещественные коэффициенты.

Пусть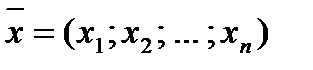

и

.

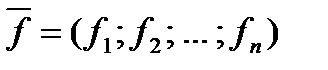Тогда

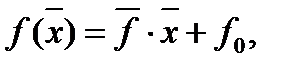
где

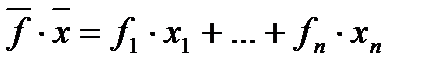
- скалярное произведение векторов в n- мерном арифметическом пространстве 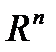. Напомним, что n-мерным арифметическим пространством 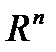называется множество всех упорядоченных наборов n вещественных чисел (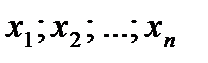) с операциями умножения на числа 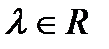и сложения, определенными по-координатно:

Элементы пространства 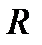ⁿ называются векторами, а само пространство – векторным или линейным.

Определение 3. Ограничения вида:

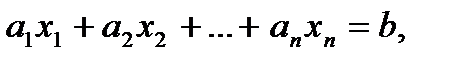
или

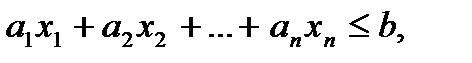
или

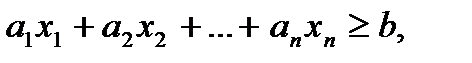
называются линейными.

Если положить 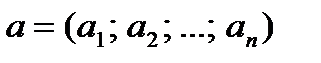, то можно записать эти ограничения в векторном виде:

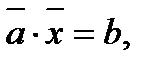
или

или

Другими словами, ограничение, имеющее вид равенства или неравенства, называется линейным, если справа стоит константа, а слева – линейная функция.

Определение 4. Ограничения вида: или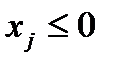

- называются тривиальными.

Эти ограничения записывают обычно в конце системы ограничений задачи линейного программирования (ЛП). Все остальные ограничения называются нетривиальными.

Таким образом, общая задача ЛП может быть представлена в виде: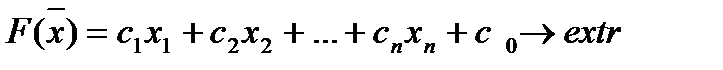

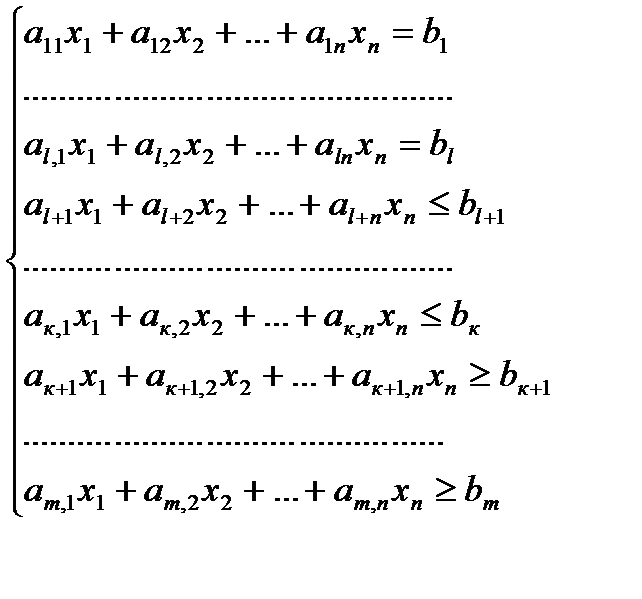(1)

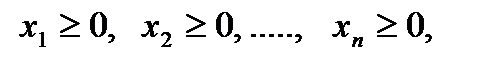
Здесь запись 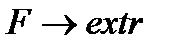означает, что следует найти экстремум, то есть максимум (max) или минимум (min), функции F.

Определение 5. Оптимизируемая в задаче ЛП функции F называется целевой функцией этой задачи.

Итак, задача ЛП определяется оптимизируемой линейной целевой функцией, нетривиальными линейными ограничениями типа равенства или неравенства и тривиальными ограничениям (которые могут отсутствовать).

Обозначение: Для сокращения записи будем далее писать 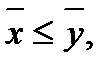если 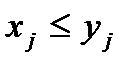для всех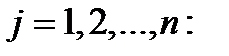

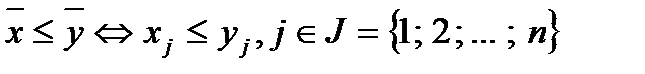
В векторном виде задача (1) имеет вид:

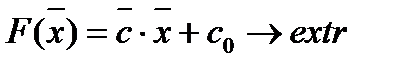
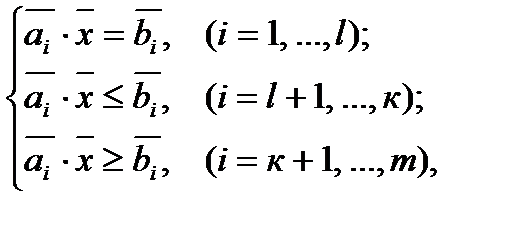(2)

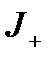где и 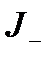- некоторые непересекающиеся подмножества множества индексов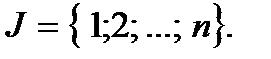

Определение 6. Матрица А= 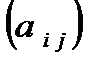, составленная из коэффициентов 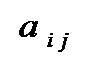системы ограничений, называется матрицей системы ограничений, а столбец - столбцом свободных членов.

Заметим, что матрица А имеет размеры m 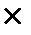n, то есть состоит из m строки n столбцов, а вектор 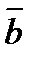состоит из одного столбца. Отметим, что вектор переменных 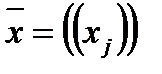состоит из одной строки (или столбца).

Определение 7. Вектор 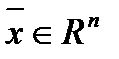называется возможным решением задачи ЛП, если он удовлетворяет всем нетривиальным ограничениям.

Определение 8. Вектор называется допустимым решением задачи ЛП, если он удовлетворяет всем ограничениям задачи ЛП, включая тривиальные.

Определение 9. Множество всех допустимых решений образует область допустимых решений (ОДР) задачи ЛП.

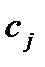Определение 10. Вектор коэффициентов при переменных 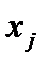целевой функции F называется вектором роста целевой функции: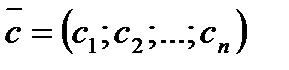

Определение 11. Свободный член 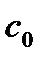целевой функции 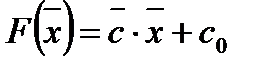называется начальным значением целевой функции.

Ясно, что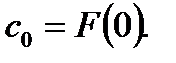

Определение 12. Допустимое решение 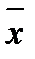называется оптимальным, если целевая функция F достигает на своего экстремума (максимума или минимума) в области допустимых решений.

Смысл названия «вектор роста» становится ясным, если заметить, что вектор является градиентом функции F, то есть вектором, составленным из частных производных функции F. Действительно, если мы продифференцируем линейную функцию

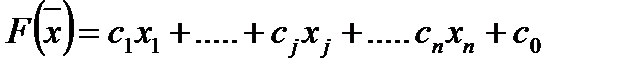
по переменной 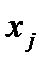, считая остальные переменные постоянными, то конечно получим :

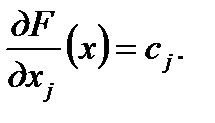(3)

Как известно из анализа, градиент функции 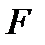указывает направление максимального роста функции в данной точке. Из (3) видно, что в линейном случае это направление не зависит от точки и совпадает с направлением вектора .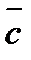

Определение 13. Линией (на плоскости) или поверхностью (в пространстве) уровня функции 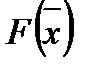называется множество точек , удовлетворяющих равенству:

,

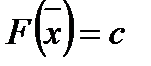где с – некоторая произвольная константа.