 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приклад застосування алгоритму АЗП по дугах, що виходять
|
|
Використовуючи алгоритм зворотньої прогонки по дугах, що виходять, знайти найкоротший шлях з вершини 1 у вершину 10 (рис. 10).
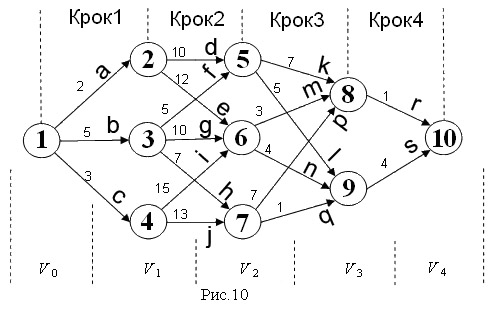
При застосуванні алгоритму зворотньої прогонки, першим планується крок 4 (останній крок). Вважаємо, що 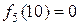 (довжина найкоротшого шляху від вершини 10 до самої себе).
(довжина найкоротшого шляху від вершини 10 до самої себе).
Планування кроку 4. Виділимо всі можливі стани, які можуть мати місце на початку кроку 4, тобто визначимо множину 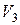 :
: 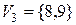 . Для цих вершин знайдемо умовні оптимальні розв’язки
. Для цих вершин знайдемо умовні оптимальні розв’язки 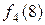 й
й 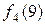 відповідно, де
відповідно, де 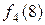 – довжина найкоротшого шляху на кроці 4 (на кроках від 4-го до (
– довжина найкоротшого шляху на кроці 4 (на кроках від 4-го до (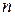 = 4)-го включно), за умови, що на початку кроку 4 система перебуває в стані (вершині) 8. Аналогічно визначається
= 4)-го включно), за умови, що на початку кроку 4 система перебуває в стані (вершині) 8. Аналогічно визначається 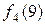 . Відповідно до виразу (1) отримаємо:
. Відповідно до виразу (1) отримаємо:
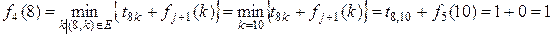 ;
; 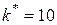 ;
;
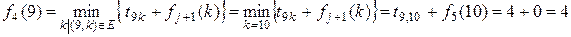 ;
; 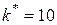 .
.

| У цьому випадку, з кожної вершини виходить тільки по одній дузі (говоримо, що в кожному стані можливий тільки один варіант розв’язку). Тобто маємо “вибір без вибору”. Така ситуація завжди має місце, якщо в останньому слої є тільки одна вершина (у нас - вершина 10). |
Заповнюємо таблицю таким чином:
Крок 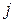
| Можливі стани на початку кроку 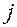 (вершини (вершини 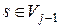 ) )
| Варіанти розв’язків 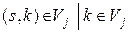
| Вартість розв’язку
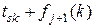
| Умовний оптимальний розв’язок | ||
| Вихідна дуга | Наступна вершина | 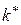
| 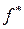
| |||
| r | 1+0=1 |  10 10
| ||||
| s | 4+0=4 |  4 4
|
У стовпчику 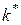 вказується вершина
вказується вершина 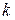 , перехід у яку з вершини
, перехід у яку з вершини 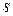 забезпечує мінімум виразу (1). У стовпчику f* вказується значення цього мінімуму – довжина найкоротшого шляху з вершини
забезпечує мінімум виразу (1). У стовпчику f* вказується значення цього мінімуму – довжина найкоротшого шляху з вершини 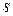 до останньої вершини 10.
до останньої вершини 10.
Планування кроку 3. На початку цього кроку система може перебувати в одному з трьох станів (вершин): 5, 6 й 7. Якщо система, наприклад, перебуває в стані (вершині) 5, то з нього можна вийти по дугах 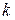 і
і 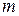 (і потрапимо у вершини 8 або 9 відповідно). Тоді для стану 5 умовний оптимальний розв’язок знаходиться таким чином:
(і потрапимо у вершини 8 або 9 відповідно). Тоді для стану 5 умовний оптимальний розв’язок знаходиться таким чином:
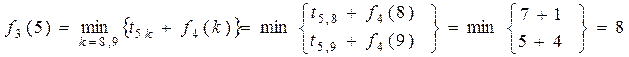 ,
,
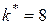 – тобто, якщо з вершини 5 перейти у вершину 8, то досягається мінімум виразу (1).
– тобто, якщо з вершини 5 перейти у вершину 8, то досягається мінімум виразу (1).

| Згадаємо одне з основних положень ДП: „ в процесі поетапного планування управління на кожному кроці повинно обиратися з урахуванням його майбутніх наслідків ”. У нашому випадку це здійснюється через урахування величин 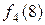 і і 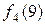 . .
|
Для стану 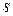 = 5 таблицю заповнюємо таким чином:
= 5 таблицю заповнюємо таким чином:
| k | 7+1=8 | |||||
| l | 5+4=9 |
Отримали: 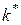 = 8,
= 8, 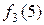 = 8.
= 8.
Аналогічні дії виконуються і для випадків, коли на початку кроку 3 система перебуває в станах 6 або 7:
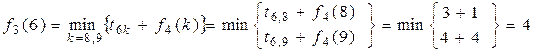 ,
, 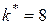 .
.
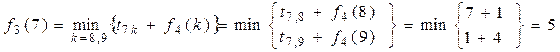 ,
,  .
.
| m | 3+1=4 | |||||
| n | 4+4=8 | |||||
| p | 7+1=8 | |||||
| q | 1+4=5 |
Аналогічно плануються кроки 2 і 1.
Повний процес розв’язку задачі наведено у таблиці 1:
Таблиця 1
Крок 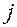
| Можливі стани на початку кроку 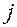 (вершини (вершини 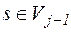 ) )
| Варіанти розв’язків 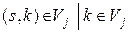
| Вартість розв’язку
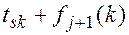
| Умовний оптимальний розв’язок | ||
| Вихідна дуга | Наступна вершина | 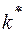
| 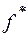
| |||
| r | 1+0=1 |  10 10
| ||||
   9 9
| s | 4+0=4 | ||||
| k | 7+1=8 | |||||
| l | 5+4=9 | |||||
| m | 3+1=4 | |||||
| n | 4+4=8 | |||||
   7 7
| p | 7+1=8 | 
| |||
| q | 1+4=5 | |||||
| d | 10+8=18 | |||||
| e | 12+4=16 | |||||
| f | 5+8=13 | |||||
  3 3
| g | 10+4=14 | 
| |||

| h | 7+5=12 | ||||
| i | 15+4=19 | |||||
| j | 13+5=18 | |||||
| a | 2 + 16=18 | |||||
  1 1
| b | 5 + 12=17 |  3 3
| |||
| c | 3 +18=21 |
Порядок формування відповіді (найкоротшого шляху) показаний стрілками.
Відповідь: найкоротший шлях: 1-3-7-9-10, довжина шляху 17.
3.3 Завдання для самостійної роботи
1. Перетворити ациклічну мережу (рис. 11) до слоїстої. Розв’язати задачу, застосувавши алгоритм зворотної прогонки.
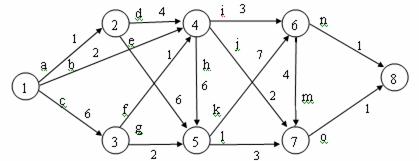 |
Рис. 11
Відповідь: найкоротший шлях 1-4-7-8, довжина 5
2. Застосувавши алгоритм зворотньої прогонки, знайти найкоротший шлях між вершинами 1 і 10 наступної мережі (рис. 12).
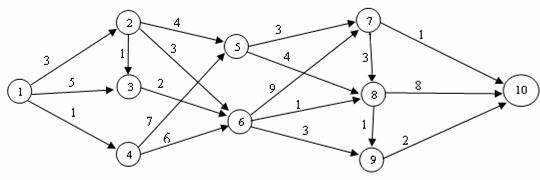 |
Рис. 12
Відповідь: найкоротші шляхи 1–2–3–6–8–9–10; 1–2–6–8–9–10, їх довжина дорівнює 10.
3. Застосувавши алгоритм зворотньої прогонки, знайти найкоротший шлях між однією з вершин першого слою (вершинами A, B або C) і вершиною K мережі, представленої на рис. 13.
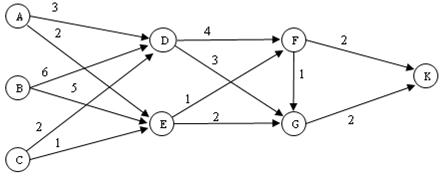
Рис. 13
Відповідь: найкоротший шлях C–E–F–K; довжина шляху 4.
У розглянутих алгоритмах обчислення починалися з кінця мережі і рухалися в напрямку її початку, тобто в напрямку, зворотньому напрямку дуг. Звідси й термін “ зворотня прогонка ” у назві алгоритму.
Задача може бути розв’язана і в іншому напрямку, тобто при русі від початку мережі до її кінця. У цьому випадку говорять про “ пряму прогонку ”.
У випадку прямої прогонки під величиною 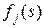 розуміємо мінімальну довжину шляху на кроках
розуміємо мінімальну довжину шляху на кроках 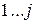 включно за умови, що наприкінці кроку
включно за умови, що наприкінці кроку 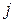 прийшли у вершину
прийшли у вершину 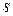 . Нехай до стану
. Нехай до стану 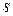 ми прийшли по дузі (
ми прийшли по дузі (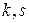 ). У цьому випадку мінімальна довжина шляху становить величину
). У цьому випадку мінімальна довжина шляху становить величину 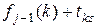 . Знайшовши мінімум по всім вхідним у вершину
. Знайшовши мінімум по всім вхідним у вершину 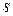 дугам, отримаємо:
дугам, отримаємо:
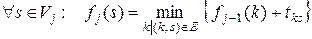 (2)
(2)
Співвідношення (2) справедливо і для 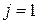 , якщо прийняти, що
, якщо прийняти, що  . З урахуванням позначень наша мета – знайти
. З урахуванням позначень наша мета – знайти 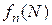 .
.
Співвідношення (1) і (2) називаються (основними) рекурентними співвідношеннями.
Дата публикования: 2014-11-04; Прочитано: 319 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
