Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующихся рядов. Абсолютная и условная сходимость рядов

Определение. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны:

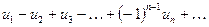, где .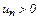

Теорема (признак Лейбница). Если в знакочередующемся ряде 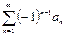выполняются два условия: 1) члены ряда убывают по абсолютной величине 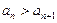. 2) предел общего члена равен нулю 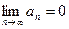, то ряд сходится, и модуль суммы этого ряда не превосходит модуля первого члена.

Доказательство:

Рассмотрим частичные суммы с четными номерами: 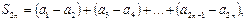разности во всех скобках неотрицательны, поэтому 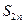– возрастающая последовательность. С другой стороны, 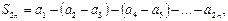поэтому 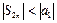, т.к. все разности в скобках неотрицательны. Ограниченная возрастающая последовательность имеет конечный предел, т.е. 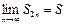причем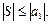

Рассмотрим предел последовательности частичных сумм с нечетными номерами:

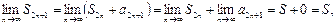т.е. и частичные суммы с нечетными номерами имеют тот же предел, т.е. ряд сходится, а т.к. 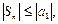и их предел не превосходит по абсолютной величине модуля первого члена ряда.

Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям признака Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

Пример. Исследовать сходимость ряда .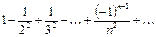

Решение. Применим признак Лейбница.

1) Члены ряда по абсолютной величине убывают: .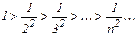

2) .

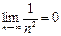Следовательно, ряд сходится.