 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры
|
|
1) Пусть функция  неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке  . Тогда исходя из геометрического смысла определенного интеграла площадь
. Тогда исходя из геометрического смысла определенного интеграла площадь  криволинейной трапеции, ограниченной кривой
криволинейной трапеции, ограниченной кривой  и прямыми
и прямыми 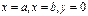 (рис. 10.2) численно равна определенному интегралу:
(рис. 10.2) численно равна определенному интегралу:
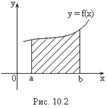
 . (11. 1)
. (11. 1)
Пример. Найти площадь фигуры, ограниченной линиями  .
.

| Решение.
1 способ. Из рисунка 11.1 видно, что искомая площадь равна:  . Найдем координаты точки . Найдем координаты точки  : :  ,
откуда для точки ,
откуда для точки  имеем имеем  , а для точки , а для точки  имеем имеем  . .
 ; ;  ; ;  
|
2 способ. Если уравнение кривой записать в виде  , то искомая площадь будет
, то искомая площадь будет  :
:  .
.
2) Если функция  неположительна и непрерывна на отрезке
неположительна и непрерывна на отрезке 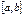 (рис. 11.2), то площадь
(рис. 11.2), то площадь

| 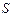 над кривой над кривой 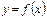 на на 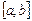 отличается знаком от определенного интеграла: отличается знаком от определенного интеграла:
 т.е т.е  . (11. 2) . (11. 2)
|
Пример. Найти площадь фигуры, ограниченной кривой 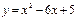 и осью абсцисс.
и осью абсцисс.
Решение. На рис. 11.3 приведена плоская фигур, ограниченная параболой  , вершина которой находится в точке
, вершина которой находится в точке  , и осью
, и осью 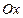 . Парабола пересекает ось
. Парабола пересекает ось  в точках с координатами
в точках с координатами 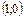 и
и  . Площадь этой фигуры, согласно формулы (11.2), равна
. Площадь этой фигуры, согласно формулы (11.2), равна
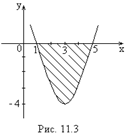
|    (ед. (ед. 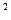 ). ).
|
3) Теорема. Если на отрезке  заданы непрерывные функции
заданы непрерывные функции  и
и  такие, что
такие, что  (рис. 11.4).
(рис. 11.4).

| Тогда площадь  фигуры, заключенной между кривыми фигуры, заключенной между кривыми 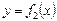 и и  на отрезке на отрезке 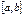 , вычисляется по формуле: , вычисляется по формуле:
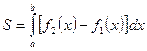 . (11.3) . (11.3)
|
Пример. Найти площадь фигуры, ограниченной линиями:

|  .
Решение. Из рис. 11.5 видно, что искомая площадь находится по формуле (11.3), полагая .
Решение. Из рис. 11.5 видно, что искомая площадь находится по формуле (11.3), полагая  . .
  . .
|
Дата публикования: 2014-11-04; Прочитано: 3496 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
