Экстремум функции двух переменных

Определение. Точка 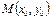называется точкой максимума (минимума) функции 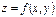, если существует окрестность точки такая, что для всех точек 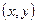этой окрестности выполняется неравенство: , .

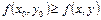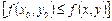Теорема (необходимое условие экстремума). Пусть точка 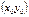- есть точка экстремума дифференцируемой функции 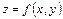. Тогда частные производные 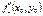и 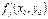в этой точке равны нулю.

Терема (достаточное условие экстремума). Пусть функция :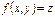

а) определена в некоторой окрестности критической точки 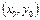, в которо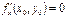й и ,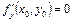

б) имеет в этой точке непрерывные частные производные второго порядка , , .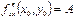

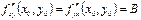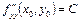Тогда, если 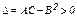, то в точке 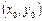функция 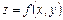имеет экстремум, причем ес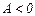ли (или 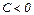) – максимум, ес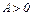ли (или 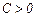) - минимум. В противном случае функция экстремума не имеет. Если 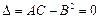, то вопрос о наличии экстремума остается открытым.

Схема исследования функции двух переменных на экстремум:

1) Найти частные производные функции и .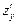

2) Решить систему уравнени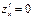й и 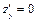и найти критические точки функции.

3) Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

4) Найти экстремумы (экстремальные значения) функции.

Пример. Исследовать функцию 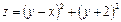на экстремум. Решение. Находим частные производные: 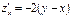, 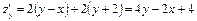. Критические точки функции находим из системы уравнений: 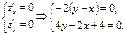Решая систему, имеем одну критическую точку 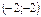. Находим частные производные второго порядка: 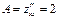, , 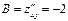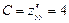. Составляем 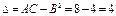. Так как 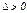и 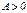, то точка 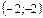есть точка минимума.