Порядок выполнения лабораторной работы с помощью метода Ньютона

1. Графически или аналитически отделить корень уравнения f(x) = 0. Убедиться, что на найденном отрезке [a,b] функция f(x) удовлетворяет условиям сходимости метода Ньютона.

2. Выбрать начальное приближение корня x₀Î[a,b] так, чтобы f¢(x₀)f²(x₀)>0.

3. Оценить снизу величину 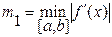, оценить сверху величину .

4. По заданному e₀ выбрать значение e для условия окончания итерационного процесса .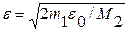

5. Составить программу вычисления корня уравнения по методу Ньютона, используя пакет MathCAD.

6. Произвести вычисления по программе.

Таблица 2.3.

Варианты заданий к лабораторной работе.

№ варианта	f(x)	№ варианта	f(x)

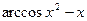
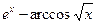
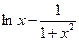
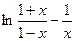
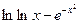
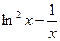
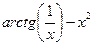
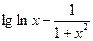
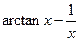
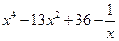
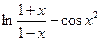
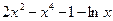
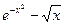
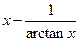
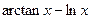
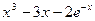
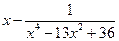
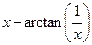
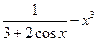
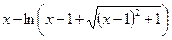
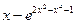
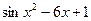
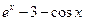
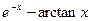
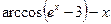
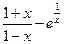
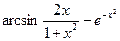
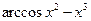
2.4. Лабораторная работа № 4.

Ускоренные методы решения нелинейных уравнений.

Для того чтобы ускорить процесс сходимости метода простых итераций (МПИ) для решения нелинейных уравнений применяют последовательности, получаемые с помощью несложных арифметических манипуляций над несколькими членами последовательности 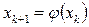, k = 0,1,2,…. Где 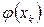- функция, связанная с f(x) таким образом, что последовательность 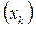сходится к единственному корню уравнения f(x) [1].

Для всех таких методов характерны многошаговость, экономичность (поскольку более быстрая сходимость по сравнению с базовой достигается без дополнительного вычисления значений функций), а также сложность исследования условий и скорости сходимости. Отсюда – отсутствие эффективных априорных оценок погрешностей. Возможны ситуации, когда новый метод окажется сходящимся, в то время как базовый для него МПИ расходится.

Рассмотрим два таких метода ускорения сходимости последовательности 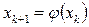. Наличие неподвижной точки ξ и дифференцируемость функции φ(x) далее всюду предполагается [1].

2.4.1. Метод Эйткена (Δ² – процесс Эйткена).

Пусть 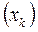- последовательность, получаемая по формуле

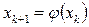(2.8)

И при условии её сходимости корень уравнения равен (с учётом погрешности)

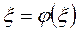(2.9),

тогда вычитая (2.8) из (2.9), имеем

а уменьшив здесь индекс на единицу, получаем

.

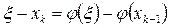К правым частям этих равенств применим формулу Лагранжа, согласно которой найдутся точки c_k и c_k-1 такие, что

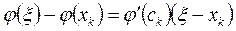
и

.

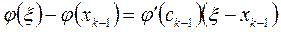Таким образом, имеют место следующие связи между ошибками соседних приближений:

,

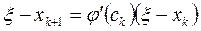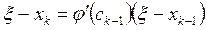
Предположим, что в той окрестности корня ξ, в которой находятся точки x_k-1 и x_k, производная 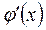меняется не очень быстро. Это допущение позволяет считать, что

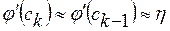, где η – некоторое число,

и значит,

, .

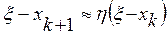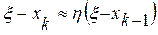Беря отношение этих приближённых равенств, избавляемся от η:

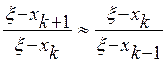, (2.10)

и разрешаем полученное приближённое уравнение относительно ξ:

.

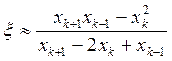Последнее выражение можно использовать на завершающем этапе применения метода простых итераций, чтобы получить более точное приближение к корню ξ с помощью трёх последних членов последовательности 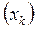. В развитие метода обозначим правую часть этого приближённого равенства через 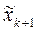и придадим его выражению другой вид:

.

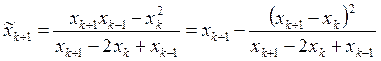Более коротко это записывается так:

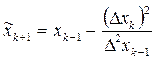, (2.11)

где 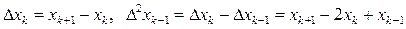- так называемые конечные разности первого и второго порядков соответственно. Отсюда название (2.11) Δ² – преобразование или Δ² – процесс Эйткена [1].

Примером реализации такого метода может служит следующий алгоритм.

Δ² – алгоритм Эйткена

Шаг 0. Ввод x₀ (начального приближения), φ(x) (исходной функции), q (оценки модуля производной), ε (допустимой абсолютной погрешности).

Шаг 1. Вычисление значений .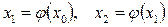

Шаг 2. Δ² – ускорение: .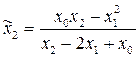

Шаг 3. Вычисление контрольного значения: .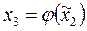

Шаг 4. Проверка на точность: если 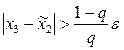, то положить 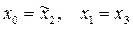, вычислить 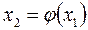и вернуться к шагу 2.

Шаг 5. Положить 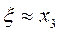(с точностью до ε).

Применяя метод Эйткена, не следует забывать о проблеме своевременного прерывания счёта из-за потерь точности при вычитании близких чисел. Подключение Δ² – ускорения на ранней стадии МПИ, когда x₀ далеко от ξ, может привести к расходимости процесса, по крайней мере, в случае, когда [1].