Введение в анализ. Понятие функции

С понятием функции вы знакомились в школьном курсе алгебры и даже умели исследовать большинство элементарных функций на предмет их основных свойств и строить их графики. Поэтому введение в математический анализ не должно казаться вам чем-то безумно новым и сногсшибательным.

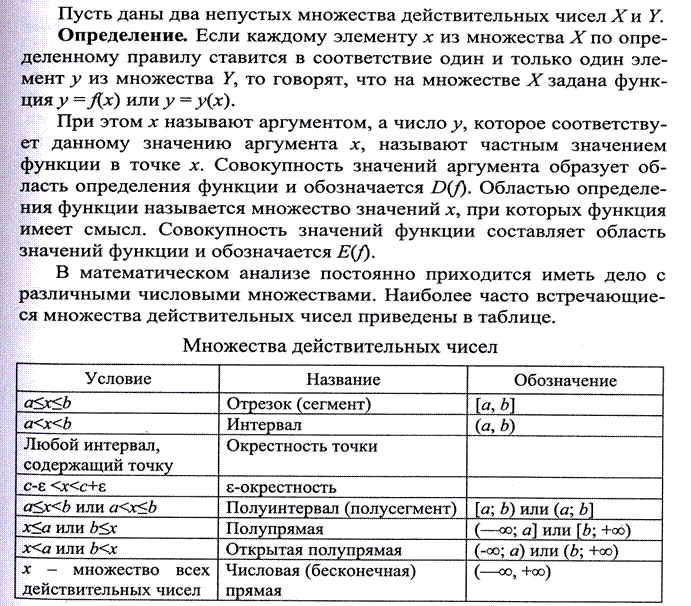
Для начала вспомним, как вводится само понятие функции.

Заметим, что введенное таким образом понятие функции — через соответствие между числовыми множествами — допускает широкие обобщения, имея в виду, что соответствие может строиться не только между числовыми множествами. Рассмотренные ранее в аналитической геометрии преобразования координат вполне можно рассматривать как соответствия между множествами точек, задаваемых как совокупность координат в соответствующем пространстве, т.е. функции точек. Если элементами множества являются векторы, то можно говорить о вектор-функциях и т.п. Предмет исследований функциональных зависимостей самого общего вида носит название функционального анализа и на сегодня представляет собой весьма развитую и в значительной степени обособленную область математики. Мы же остановимся на функциях, являющихся соответствиями только между числовыми множествами. Но, даже не заплывая на самые глубокие места водоема, полезно помнить, что они есть и
знать, где они находятся.

Вспомним основные свойства функций, которые необходимы для их исследования. Наиболее приятное из них, хотя и носящее несколько скучное наименование — это свойство монотонности. Оно включает в себя возрастание, убывание, а также невозрастание и неубывание. Введем для всех них соответствующие определения.

Как видно, разнообразие вводимых понятий обусловлено строгостью или нестрогостью неравенств, связывающих между собой соответствующие значения функций. Поэтому часто эта строгость и нестрогость подчеркивается специально.

С понятием монотонности тесно связано понятие четности и нечетности функций.

В определенном смысле антиподами монотонных функций являются периодические функции, для которых одному значению функции соответствует много значений аргумента. Наиболее типичным примером периодических функций являются тригонометрические функции.

Важнейшим понятием, позволяющим выстроить мостик между элементарной и высшей математикой, является понятие предела функции.

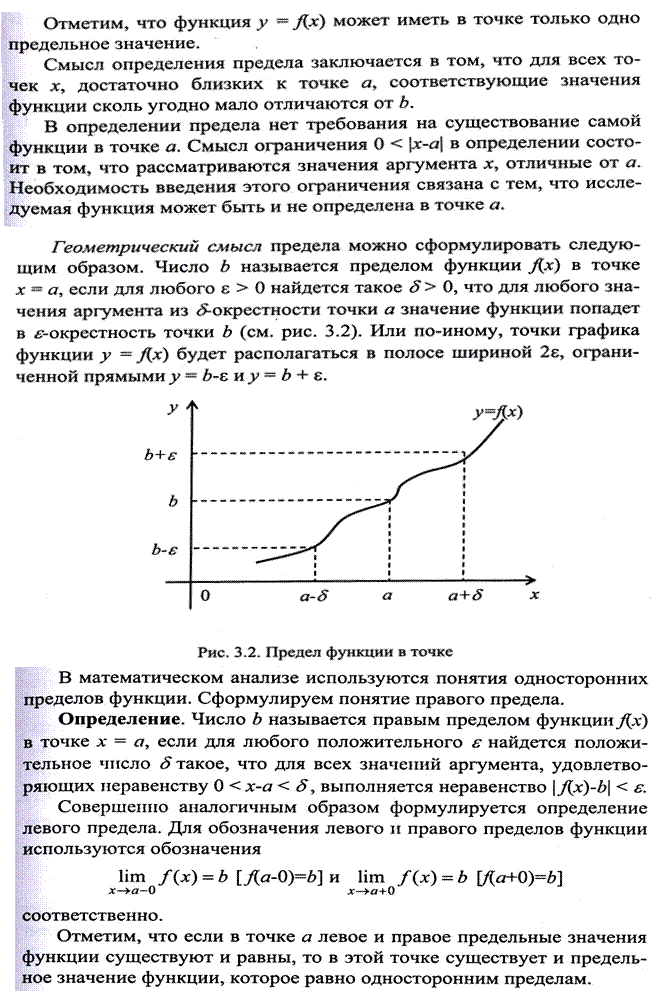
Замечание, касающееся того, что в самой предельной точке функция не обязана быть определена, является весьма существенным. Оно позволяет ввести такие принципиально важные понятия, как бесконечно большие и бесконечно малые функции, а также возможность отсутствия предела в данной точке.

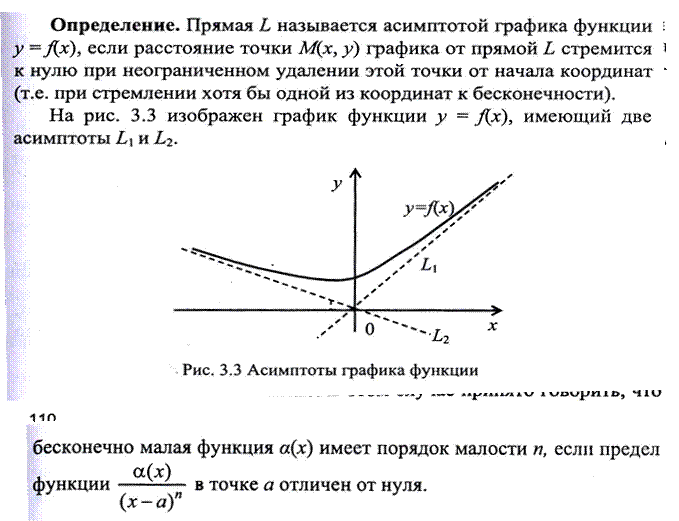
Рассматривая в аналитической геометрии кривые второго порядка, мы с вами уже имели дело с асимптотами. Теперь, опираясь на понятие предела функции, мы можем ввести строгое и обобщенное понятие асимптоты.

Еще одним важнейшим понятием, необходимым для исследования функций, является непрерывность.

Коль скоро мы ввели понятие непрерывности, логично классифицировать точки разрыва функций.

Точки разрыва принято различать следующим образом: точки устранимого разрыва, точки разрыва первого рода и точки разрыва второго рода. Все эти случаи означают, что в самой точке разрыва функция изначально не определена.

Разрыв первого рода иначе называют скачком.

Определение. Точка а называется точкой разрыва второго рода функции 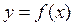, если в этой точке или не существует хотя бы одного одностороннего предела функции, или же хотя бы с одной стороны функция имеет бесконечный предел (является бесконечно большой).

Наконец, для полноты картины непрерывности введем понятие кусочно-непрерывной функции.

Для дальнейших действий с функциями нам понадобятся еще понятия обратной функции и сложной функции.