Временная форма представления сигнала

Временным представлением сигнала называют такое разложение сигнала u(t), при котором в качестве базис­ных функций используются единичные импульсные функ­ции — дельта-функции. Математическое описание такой функции задается соотношениями

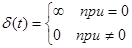(1.9)

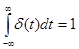
где d(t)— дельта-функция, отличная от нуля в начале координат (при t = 0).

Для более общего случая, когда дельта-функция отличается от нуля в момент времени t = x₁ (рис.),

имеем

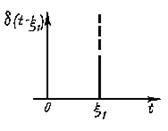
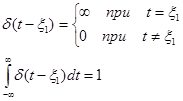(1.10)

Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала u(t) в конкретный момент времени x₁:

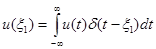(1.11)

Равенство (1.11) справедливо для любого текущего момента времени t. Заменив £i на t и приняв в качестве переменной интегрирования |, получим

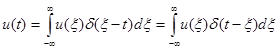(1.12)

Таким образом, функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.

Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующим значениям входного сигнала.

С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через u_n(t) функцию, равную u(kDt) в точках t = kDt и нулю в остальных точках, запишем:

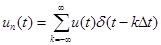
где Dt — период следования импульсов.

Поскольку умножение u{t) на дельта-функцию в момент времени t = kDt соответствует получению отсчета этой функции, u_n(kAt) может представлять результат равномерной дискретизации функции u(t).

Дельта-функцию d(x) в точке x = 0 можно рассматривать как предел множества действительных непрерывных функций, подобных функциям Гаусса:

(2.2)

При этом вместе с величиной а максимальное значение функции Гаусса стремится к бесконечности, полуширина (1/ а) стремится к нулю, в то время как интеграл этой функции всегда равен едини­це. Отсюда следует, что дельта-пункция удобна для описания лю­бой функции, имеющей форму пика с пренебрежимо (в эксперименте) малой полушириной.

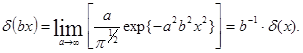Подобным же образом дельта-функция с∙d(х) используется для описания резкого пика, интеграл которого равен с. Для более ясного понимания или

доказательства различных соотношений удобно определять дельта-функцию как предел ряда функций.

Можно определить дельта-функцию в двух измерениях d(х, у), которая равна нулю всюду, кроме точки х = у = 0, и для которой:

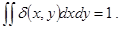
Подобным же образом можно определить дельта-функцию для любого числа измерений d(r) или d(r—a), где r и а — векторы n -мерного пространства.

Заметим, что в двух измерениях d(х) является линией, а в трех измерениях — плоскостью.

Отметим другое важное определение дельта-функции:

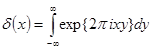
(2.3)

которое встретится позже в связи с рассмотрением фурье-преобра-зований.