 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тема №6: Циклические коды. Коды БЧХ
|
|
Циклические коды относятся к классу линейных систематических кодов. Они названы циклическими потому, что циклический сдвиг разрешенной кодовой комбинации приводит также к разрешенной кодовой комбинации. Например, если 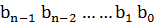 – разрешенная кодовая комбинация, тогда после ее циклической перестановки получим новую кодовую комбинацию
– разрешенная кодовая комбинация, тогда после ее циклической перестановки получим новую кодовую комбинацию 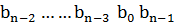 , которая также является разрешенной.
, которая также является разрешенной.
Циклическое свойство этих кодов позволило упростить реализацию кодеров и декодеров и дало возможность в системах связи строить эффективные блочные коды большой длины с большим количеством разрешенных кодовых комбинаций.
В циклическом коде кодовые комбинации представляются в виде полинома (многочлена) некоторой степени.
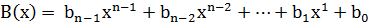 ,
,
где x - основание системы счисления;
bi – символы кода в данной системе счисления.
Например: Двоичная кодовая комбинация 010101 представляется многочленом вида 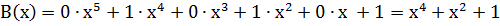 .
.
Представление кодовых комбинаций в виде многочлена позволяет установить однозначное соответствие между ними и свести действия над кодовыми комбинациями к действиям над многочленами. Над многочленами можно выполнять все алгебраические действия, только учитывая, что для двоичных многочленов сложение производится по модулю 2.
Пример:
1. Сложение:
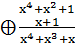 ;
; 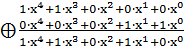 ;
; 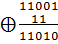
2. Умножение:
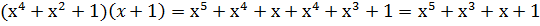
Здесь коэффициенты при равных x складываются по модулю 2.
3. Деление:
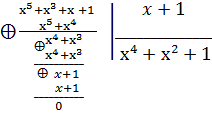 ;
; 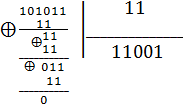
Циклический сдвиг некоторого многочлена соответствует простому умножению его на х.
Умножив, например, многочлен 
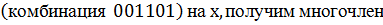
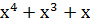 , соответствующий комбинации
, соответствующий комбинации 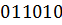 .
.
Циклические коды характеризуются тем, что многочлены разрешенных кодовых комбинаций 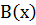 делятся без остатка на так называемый порождающий многочлен P(x).
делятся без остатка на так называемый порождающий многочлен P(x).
Порождающим многочленом может быть любой многочлен P(x) степени r=n-k, который делит без остатка двучлен (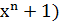 . Например, порождающий многочлен x2+x+1 делит без остатка двучлен x6+1, а многочлен x3+x+1 делит двучлен x7+1.
. Например, порождающий многочлен x2+x+1 делит без остатка двучлен x6+1, а многочлен x3+x+1 делит двучлен x7+1.
В теории циклических кодов доказывается, что наилучшими свойствами обладают коды с порождающими многочленами в виде неприводимых (примитивных) многочленов. Они, как и простые числа, делятся только на себя и на 1.
Процесс циклического кодирования сводится к отысканию многочлена 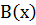 по известным многочленам А(x) и P(x), который бы делился на P(x) без остатка. Здесь А(х) - многочлен степени k-1, соответствующий информационной последовательности символов.
по известным многочленам А(x) и P(x), который бы делился на P(x) без остатка. Здесь А(х) - многочлен степени k-1, соответствующий информационной последовательности символов.
Очевидно, что правило построения циклического кода можно представить в виде произведения информационной кодовой комбинации на порождающий многочлен:
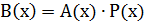 .
.
| Степень многочлена r | Порождающий многочлен P(x) |
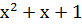
| |
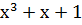

| |
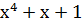
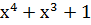
| |
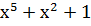
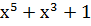
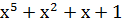
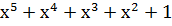
| |
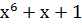
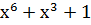
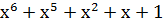
| |
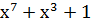
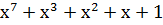
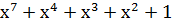
| |

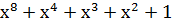
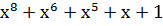
| |

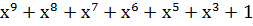
| |
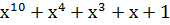
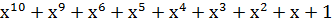
| |
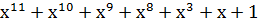

|
Пример. Дано информационное слово 0111, построить разрешенную кодовую комбинацию кода (7,4).
Найдем r = n-k = 7-4 = 3. По таблице выберем порождающий многочлен, причем при r=3 любой из двух, например 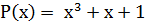 . Тогда A(x)=x2+x+1 и
. Тогда A(x)=x2+x+1 и 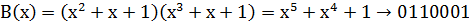 .
.
Если построить все разрешенные кодовые комбинации, перебирая все возможные четырехразрядные информационные слова, то из полученного множества комбинаций можно увидеть, что они обладают циклическим свойством. (Проверить самостоятельно и на практическом занятии).
| Комбинации | 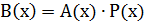
|
(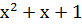 )·1= )·1= 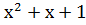 → 000111 → 000111
| |
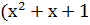 )(x+1) = )(x+1) = 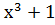 → 001001 → 001001
| |
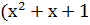 )·x = )·x = 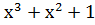 → 001110 → 001110
| |
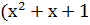 ) ) 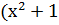 ) = ) = 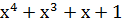 → 011011 → 011011
| |
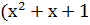 )·x2 = )·x2 = 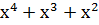 → 011100 → 011100
| |
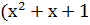 ) ) 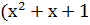 ) = ) = 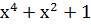 → 010101 → 010101
| |
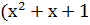 ) ) 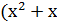 ) = ) = 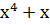 → 010010 → 010010
| |
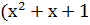 )( )(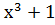 ) = ) = 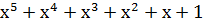 →111111 →111111
| |
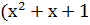 )· )· 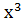 = = 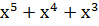 = 111000 = 111000
| |
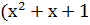 ) ) 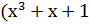 ) = ) = 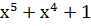 → 110001 → 110001
| |
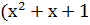 ) ) 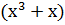 = = 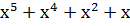 →110110 →110110
| |
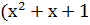 ) ) 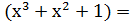 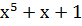 →100011 →100011
| |
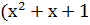 )( )(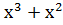 ) = ) = 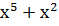 →100100 →100100
| |
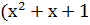 ) ) 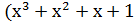 ) = ) = 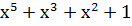 → 101101 → 101101
| |
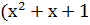 ) ) 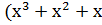 ) = ) = 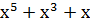 → 101010 → 101010
|
Однако полученный таким образом код является неразделимым, поскольку информационные и проверочные символы в разрешенных кодовых комбинациях окажутся перемешанными, что затрудняет процесс декодирования.
На практике применяется другой способ нахождения многочлена 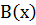 , а именно:
, а именно:
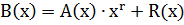 ,
,
где 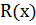 - остаток от деления произведения
- остаток от деления произведения 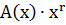 на порождающий многочлен P(x).
на порождающий многочлен P(x).
Алгоритм построения разрешенных кодовых комбинаций, таким образом, сводится к следующему:
1. Представляем информационные кодовые комбинации длиной k d виде многочленов A(x).
2. Умножаем A(x) на xr, т.е. осуществляем сдвиг кодовой комбинации на r разрядов.
3. Делим 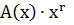 на порождающий многочлен P(x) степени r, чтобы получился остаток R(x).
на порождающий многочлен P(x) степени r, чтобы получился остаток R(x).
4. Добавляем R(x) к 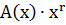 .
.
5. Представляем многочлен 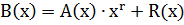 в виде кодовой комбинации.
в виде кодовой комбинации.
Пример. Построим разрешенную кодовую комбинацию циклического кода (7,4) указанным способом.
В качестве информационной кодовой комбинации возьмем рассмотренную ранее 0111 и тот же порождающий многочлен
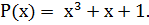
Тогда
1. 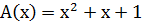
2. 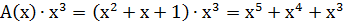
3. 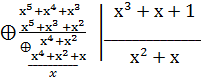 ;
; 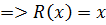
4. 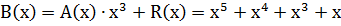
5. B(x) 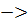 0111010
0111010
Здесь код получился разделимым.
Если по этому алгоритму построить все разрешенные комбинации по заданным четырехразрядным информационным словам, то можно будет увидеть, что такой код обладает циклическим свойством и является разделимым (сделать это самостоятельно и на практическом занятии).
Обнаружение ошибок при циклическом декодировании сводится к делению принятой кодовой комбинации на тот же порождающий многочлен, который используется при кодировании. Если в принятой комбинации нет ошибок, то деление произойдет без остатка. Если при делении получится остаток, то это свидетельствует о наличии ошибки.
Пример. В качестве разрешенной кодовой комбинации возьмем 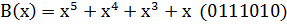 ; P(x)=
; P(x)= 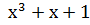 .
.
Пусть в принятой комбинации нет ошибок, тогда
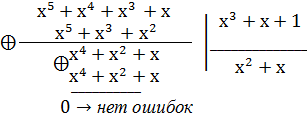
Пусть в принятой комбинации есть ошибка в старшем разряде: 1111010, то
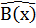 =
= 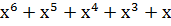
При этом,
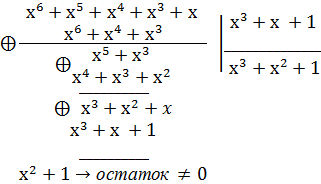
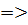 R(x) =
R(x) = 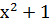 (101). - есть ошибка в принятой кодовой комбинации.
(101). - есть ошибка в принятой кодовой комбинации.
Исправление ошибок при циклическом декодировании основано на анализе остатка R(x), полученного при делении принятой кодовой комбинации 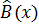 на порождающий полином P(x). Этот остаток называют синдромом.
на порождающий полином P(x). Этот остаток называют синдромом.
Следует отметить, что для всех разрешенных кодовых комбинаций ошибка на одной и той же позиции дает одинаковый остаток. Поэтому ошибки можно исправлять на основе соответствий синдрома и номера ошибочной позиции в кодовой комбинации, как при декодировании линейных систематических кодов (нециклических).
Однако свойство цикличности позволяет избавиться от запоминания в памяти декодера синдромов для исправления ошибок и тем самым существенно упростить процедуру декодирования.
Существует несколько методов декодирования циклических кодов. Рассмотрим один из них:
1.Принятую кодовую комбинацию 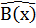 делят на порождающий многочлен и вычисляют вес остатка g, т.е. подсчитывают число единиц в остатке R(x). Если в результате вес окажется таким, что g ≤ t, где t-число исправленных ошибок, то принятую кодовую комбинацию складывают по модулю 2 с остатком, что и она будет исправленной.
делят на порождающий многочлен и вычисляют вес остатка g, т.е. подсчитывают число единиц в остатке R(x). Если в результате вес окажется таким, что g ≤ t, где t-число исправленных ошибок, то принятую кодовую комбинацию складывают по модулю 2 с остатком, что и она будет исправленной.
2. Если в результате деления вес остатка g > t, то проводят циклический сдвиг принятой кодовой комбинации вправо. Полученную комбинацию опять делят на P(x) и вычисляют вес остатка. Если вес нового остатка g ≤ t, то данную комбинацию складывают с остатком по модулю 2 и полученную комбинацию циклически сдвигают влево на один разряд, что дает исправленную кодовую комбинацию.
3. Если после второго деления вес нового остатка g > t, то процедуру циклического сдвига вправо, деления на P(x) и вычисления веса остатка продолжают до тех пор, пока не будет выполнено условие g ≤ t. Как только это условие выполняется на некотором i-ом шаге, полученную комбинацию суммируют с остатком и производят обратный циклический сдвиг суммы на i разрядов. В итоге получим исправленную кодовую комбинацию.
Пример. Дан циклический код (7,4) с порождающим многочленом P(x)= 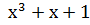 .
.
1. Пусть передана комбинация 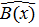 = 1010111, которая исказилась в третьем справа символе так, что принятая комбинация
= 1010111, которая исказилась в третьем справа символе так, что принятая комбинация 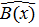 = 1010111. Учитывая, что P(x)=1011,найдем остаток от деления g=
= 1010111. Учитывая, что P(x)=1011,найдем остаток от деления g= 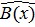 /P(x)
/P(x)
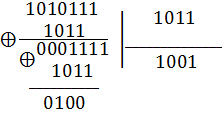
0100 
Считая t=1, получим g=t, найдем исправленную комбинацию B(x)= 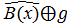
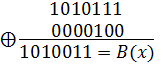
2. Пусть ошибка произошла в пятом разряде (искажен информационный символ), т.е. 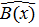 = 1000011. Тогда g=
= 1000011. Тогда g= 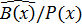
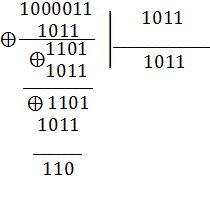
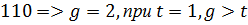
Выполним циклический сдвиг вправо и снова найдем остаток.
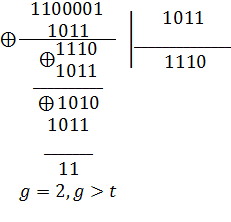
Еще сдвиг и деление:
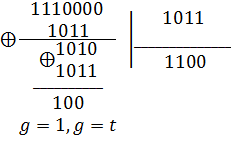
Теперь, после двух сдвигов вправо вес позволяет искать исправленную комбинацию путем сложения и обратного сдвига на два разряда:
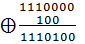 1-ый сдвиг влево
1-ый сдвиг влево 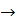 1101001
1101001 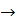 2-ой сдвиг влево
2-ой сдвиг влево 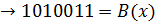
Среди циклических кодов особое место занимают коды БЧХ (Боуза-Чоудхури-Хоквингем), которые обладают хорошими корректирующими способностями.
Длина кодовой комбинации кодов БЧХ может быть определена из выражения: 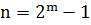 , где
, где 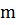 - любое целое число. Таким образом, кодовые комбинации циклического кода БЧХ могут содержать 7, 15, 31, 63, 127 и т. д. символов.
- любое целое число. Таким образом, кодовые комбинации циклического кода БЧХ могут содержать 7, 15, 31, 63, 127 и т. д. символов.
Особенностью кодов БЧХ является специальный выбор порождающего многочлена, который находится как наименьшее общее кратное (НОК) неприводимых многочленов. Наименьшим общим кратным совокупности неприводимых многочленов называют многочленом наименьшей степени, который делится на каждый из них. Во многих случаях такой многочлен находится в результате произведения неприводимых многочленов.
Например, для кода БЧХ длиной n=31 с кодовым расстоянием dmin=5 порождающий многочлен может быть представлен следующим образом:
1. Неприводимые многочлены для r=5
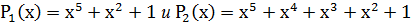
2. Их произведение:
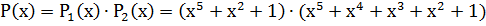 =
= 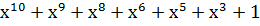
На практике коды БЧХ исследованы достаточно подробно, а порождающие многочлены, необходимые для их построения при различных значениях n сведены в специальные таблицы.
Дата публикования: 2014-11-04; Прочитано: 2018 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
