Основные положения, допущения и обозначения

Лекции по теории упругости

(заочный факультет)

Лекция 1. Основы теории упругости

Основные положения, допущения и обозначения

Теория упругости имеет целью аналитическое изучение напряженно-деформированного состояния упругого тела. С помощью теории упругости могут быть проверены решения, полученные с использованием допущений сопротивления ма­териалов, и установлены границы применимости этих решений. Иногда разделы теории упругости, в которых, как и в сопротив­лении материалов, рассматривается вопрос о пригодности де­тали, но с использованием достаточно сложного математического аппарата (расчет пластин, оболочек, массивов), относят к при­кладной теории упругости.

В настоящей главе изложены основные понятия математиче­ской линейной теории упругости. Применение математики к опи­санию физических явлений требует их схематизации. В математической теории упругости задачи решаются с возможно меньшим числом допущений, что усложняет мате­матические приемы, применяемые для решения. В линейной тео­рии упругости предполагается существование линейной зави­симости между составляющими напряжениями и деформациями. Для ряда материалов (резина, некоторые сорта чугуна) такая зависимость даже при малых деформациях не может быть принята: диаграмма s - e в пределах упругости имеет одинако­вые очертания как при нагружении, так и при разгрузке, но в обоих случаях криволинейна. При исследовании таких материалов необходимо пользоваться зависимостями нелинейной теории упру­гости.

В математической линейной теории упругости исходят из следующих допущений:

1. О непрерывности (сплошности) среды. При этом атомистическая структура вещества или наличие каких-либо пустот не учитывается.

2. О естественном состоянии, на основании которого началь­ное напряженное (деформированное) состояние тела, возникшее до приложения силовых воздействий, не учитывается, т. е. предполагается, что в момент нагружения тела деформации и напряжения в любой его точке равны нулю. При наличии на­чальных напряжений это допущение будет справедливым, если только к результирующим напряжениям (сумме начальных и возникших от них из воздействий) могут быть применены зависимости линейной теории упругости.

3. Об однородности, на основании которого предполагается, что состав тела одинаков во всех точках. Если применительно к металлам это допущение не дает больших погрешностей, то в от­ношении бетона при рассмотрении малых объемов оно может при­вести к значительным погрешностям.

4. О шаровой изотропности, на основании которого считается, что механические свойства материала одинаковы по всем направ­лениям. Кристаллы металла не обладают таким свойством, но для металла в целом, состоящего из большого числа мелких кри­сталлов, можно считать, что эта гипотеза справедлива. Для ма­териалов, обладающих различными механическими свойствами в разных направлениях, как, например, для слои­стых пластиков, разработана теория упругости ортотропныхи анизотропных материалов.

5. Об идеальной упругости, на основании которого предпола­гается полное исчезновение деформации после снятия нагрузки. Как известно, в реальных телах при любом нагружении возникает остаточная деформация. Поэтому допущение следует считать при­менимым, если остаточная деформация не превышает условно заданной нормы.

6. О линейной зависимости между составляющими деформа­циями и напряжениями.

7. О малости деформаций, на основании которого предпола­гается, что относительные линейные и угловые деформации малы по сравнению с единицей. Для таких материалов, как резина, или таких элементов, как спиральные пружины, создана теория больших упругих деформаций.

При решении задач теории упругости пользуются теоремой о единственности решения: если заданные внешние поверхностные и объемные силы находятся в равновесии, им соответствует одна единственная система на­пряжений и перемещений. Положение о единственности решения справедливо, если только справедливы допущение о естественном состоянии тела (иначе возможно бесчисленное количество решений) и допущение о линейной зависимости между деформациями и внешними силами.

При решении задач теории упругости часто пользуются принци­пом Сен-Венана: если внешние силы, приложенные на небольшом участке упругого тела, заменить действующей на том же участке статически эквивалентной си­стемой сил (имеющей тот же главный вектор и тот же главный момент), то эта замена вызовет лишь изменение местных де­формаций.

В точках, достаточно удаленных от мест приложения внешних нагрузок, напряжения мало зависят от способа их приложения. Нагрузка, которая в курсе сопротивления мате­риалов схематически выражалась на основании принципа Сен-Венана в виде силы или сосредоточенного момента, на самом деле представляет собой нормальные и касательные напряжения, распределенные тем или иным способом на определенном участке поверхности тела. При этом одной и той же силе или паре сил может соответствовать различное распределение напряже­ний. На основании принципа Сен-Венана можно считать, что из­менение усилий на участке поверхности тела почти не отражается на напряжениях в точках, удаленных на достаточно большое расстояние от места приложения этих усилий (по сравнению с линейными размерами нагруженного участка).

Положение исследуемой площадки, выделенной в теле (рис. 1), определяется направляющими косинусами нормали N к пло­щадке в выбранной системе прямоугольных осей координат х, у и z.

Если Р — равнодействующая внутренних сил, действующих по элементарной площадке 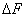, выделенной у точки А, то полное напряжение р_N в этой точке по площадке с нормалью N опре­деляется как предел отношения в следующей форме:

.

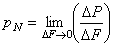Вектор р_N можно разложить в пространстве на три взаимно перпендикулярные составляющие.

А б

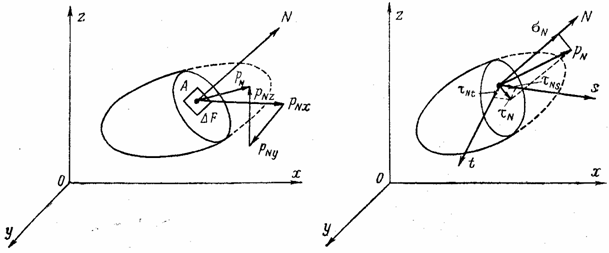
Рис. 1

1. На составляющие р_Nx, р_Ny и р_Nz по направлениям трех осей (рис. 1, а). Эти состав­ляющие положительны, если совпадают по направлению с поло­жительными направлениями соответствующих осей. Согласно рис. 1, а

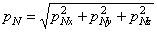. (1.1,а)

2. На составляющие , 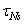и 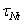по направлениям нормали к площадке (нормальное напряжение) и двух взаимно перпенди­кулярных осей s и t (рис. 1, б), лежащих в плоскости площадки (касательные напряжения). Согласно рис.1, б

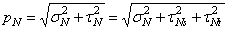. (1.1,б)

Если сечение тела или площадка 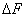параллельны одной из плоскостей координат, например у0z (рис. 2), то нормалью к этой площадке будет третья ось координат х и составляющие напря­жения будут иметь обозначения 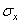, 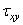и .

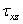Нормальное напряжение положительно, если оно растяги­вающее, и отрицательно, если оно сжимающее. Знак касатель­ного напряжения определяется с помощью следующего правила: если положительное (растягивающее) нормальное напряжение по площадке дает положительную проекцию, то касательное на­пряжение по той же площадке считается положительным при условии, что оно тоже дает положительную проекцию на соот­ветствующую ось; если же растягивающее нормальное напря­жение дает отрицательную проекцию, то положительное касательное напряжение тоже должно давать отрицательную про­екцию на соответствующую ось.

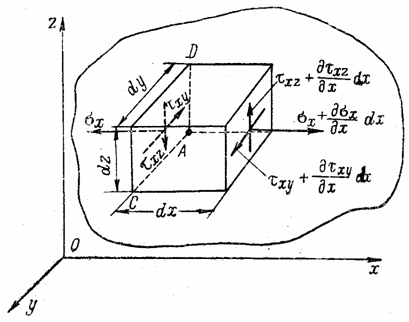
Рис. 2

На рис. 3, например, все составляющие напряжения, дейст­вующие по граням элементарного параллелепипеда, совпадаю­щим с плоскостями координат, положительны.

Рис. 3

Чтобы определить напряженное состояние в точке упругого тела, необходимо знать полные напряжения р_N по трем взаимно перпендикулярным площадкам, проходящим через эту точку. Так как каждое полное напряжение можно разложить на три составляющие, напряженное состояние будет определено, если будут известны девять составляющих напряжений. Эти составляю­щие можно записать в виде матрицы

,

называемой матрицей компонентов тензора напряжений в точке.

В каждой горизонтальной строчке матрицы записаны три со­ставляющих напряжения, действующих по одной площадке, так как первые значки (название нормали) у них одинаковые. В каждом вертикальном столбце тензора записаны три напря­жения, параллельных одной и той же оси, так как вторые значки (название оси, параллельно которой действует напряжение) у них одинаковые.