Показательная форма комплексного числа

В различных разделах современной математики, а также ее приложениях применяется показательная форма комплексного числа. В основе показательной формы лежит формула Эйлера, устанавливающая связь между тригонометрическими функциями действительного аргумента и показательной функцией мнимого аргумента.

Первая формула Эйлера (без вывода):

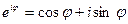, (1.15) где е – иррациональное число, принятое за основание натуральных логарифмов (е» 2,718).

Если в формуле 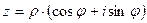произвести замену по формуле (1.15), то получим 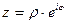. Это и есть показательная форма комплексного числа 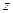. В этой записи 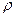− модуль комплексного числа, 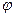− его аргумент. Заменим в формуле (1.15) 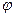на - 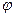, получим вторую формулу Эйлера:

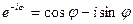. (1.16)

Из формул (1.15) и (1.16) следует, что

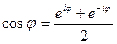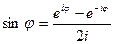, . (1.17)

Равенства (1.17) также называются формулами Эйлера и выражают тригонометрические функции действительного переменного 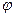через показательные функции мнимого аргумента. Формулы (1.17) справедливы и тогда, когда 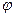заменяется любым комплексным числом 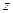, т. е. 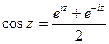, 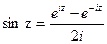. Эти равенства принимают за определение косинуса и синуса комплексного аргумента.

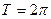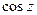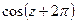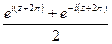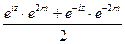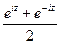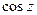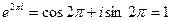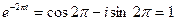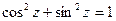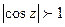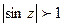Тригонометрические функции комплексного переменного также периодичны, причем период . Покажем это для функции . Действительно, = = = = , так как по формулам Эйлера , . Примечательно, что все формулы обычной тригонометрии сохраняют свою силу в комплексной плоскости, например, . Однако в отличие от действительных чисел могут иметь место неравенства и . Например,

.

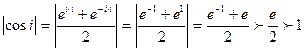МНОГОЧЛЕНЫ