 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Перша важлива границя
|
|
Приклади.
1. Якщо 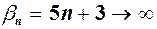 при
при 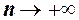 , то
, то 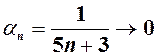 при
при 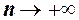 .
.
2. Якщо 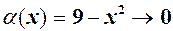 при
при 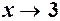 , то
, то 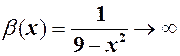 при
при 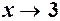 .
.
3.3 Границя послідовності. Границя функції
Нагадаємо, що закон, за яким кожному натуральному числу 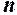 ставиться у відповідність число
ставиться у відповідність число 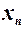 , визначає функцію натурального аргумента
, визначає функцію натурального аргумента 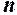 або послідовність чисел
або послідовність чисел 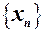 .
.
Означення 1. Число 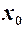 називається границею послідовності
називається границею послідовності 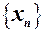 при
при 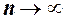 (позначається
(позначається 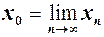 ), якщо для довільного
), якщо для довільного 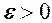 існує номер
існує номер 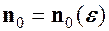 , що залежить від
, що залежить від  , такий, що для всіх наступних номерів
, такий, що для всіх наступних номерів 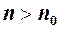 виконується нерівність
виконується нерівність
 ,
,
або скорочено:
 (14)
(14)
Якщо число 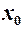 є границею послідовнсті
є границею послідовнсті 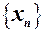 при
при  , то ще прийнято говорити, що послідовність
, то ще прийнято говорити, що послідовність 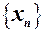 збігається до числа
збігається до числа 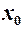 .
.
Наприклад, послідовність 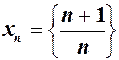 має своєю границею число
має своєю границею число  , тобто
, тобто 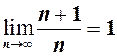 .
.
Справді, розглянемо різницю
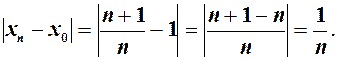
Тепер для як завгодно малого  , наприклад,
, наприклад, 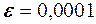 , можна підібрати номер
, можна підібрати номер  , що залежить від
, що залежить від  , розв’язавши в даному випадку нерівність
, розв’язавши в даному випадку нерівність 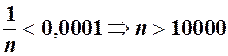 . Отже, якщо взяти
. Отже, якщо взяти 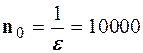 , то тепер для всіх номерів
, то тепер для всіх номерів 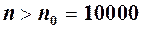 маємо
маємо
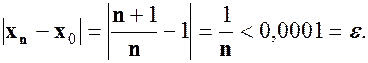
Оскільки 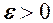 можна вибирати як завгодно малим, то число
можна вибирати як завгодно малим, то число  є границею послідовності
є границею послідовності 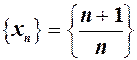 при
при  , або ж послідовність
, або ж послідовність 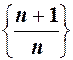 при
при  збігається до числа
збігається до числа  .
.
Означення границі для послідовності, як для функції натурального (дискретного) аргумента, легко перенести і на функцію неперервного аргумента.
Означення 2. Число 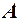 називається границею функції
називається границею функції  в точці
в точці 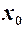 , якщо ця функція визначена в деякому околі точки
, якщо ця функція визначена в деякому околі точки 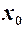 , за винятком, можливо, самої точки
, за винятком, можливо, самої точки 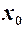 , і якщо границя послідовності
, і якщо границя послідовності 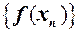 існує і дорівнює
існує і дорівнює 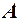 , яка б не була послідовність
, яка б не була послідовність 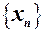 , збіжна до
, збіжна до 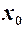 і така, що
і така, що 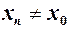 для всіх
для всіх 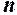 . Таким чином,
. Таким чином,
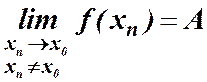 .
.
Ця границя 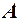 повинна бути однаковою для всіх таких послідовностей, вона і є границею
повинна бути однаковою для всіх таких послідовностей, вона і є границею 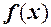 .
.
Границю функції можна означити безпосередньо, не користуючись границею послідовності.
Означення 3. Число 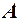 називається границею функції
називається границею функції  при
при 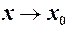 , якщо
, якщо 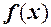 визначена в деякому околі точки
визначена в деякому околі точки 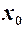 , за винятком, можливо, самої точки
, за винятком, можливо, самої точки 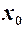 , і якщо для довільного
, і якщо для довільного 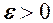 існує число
існує число 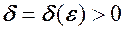 , що залежить від
, що залежить від  , таке, що із нерівності
, таке, що із нерівності 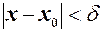 випливає нерівність
випливає нерівність  , позначається
, позначається
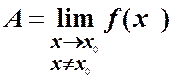 ,
,
тобто
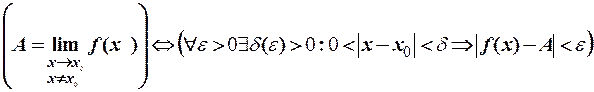 (15)
(15)
Означення 3 границі функції можна замінити більш спрощеним, яке на перших порах легше запам’ятовується.
Означення 4. Число  називається границею функції
називається границею функції  при
при 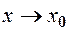 , якщо
, якщо  визначена в деякому околі точки
визначена в деякому околі точки 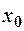 , за винятком, можливо, самої точки
, за винятком, можливо, самої точки 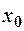 , і якщо із того, що різниця
, і якщо із того, що різниця 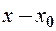 нескінченно мала випливає, що різниця
нескінченно мала випливає, що різниця 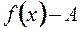 теж нескінченно мала, тобто
теж нескінченно мала, тобто
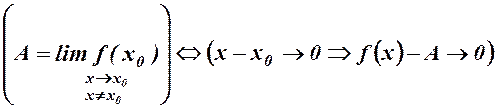 (16)
(16)
Вияснимо геометричний зміст означення 3, скориставшись графіком функції (див. рис.21)
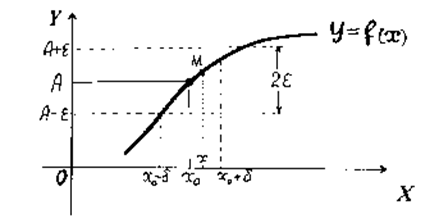
Рис. 21
Припустимо, що при 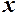 прямуючому до
прямуючому до 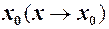 , функція
, функція  прямує до границі
прямує до границі 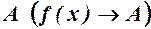 , тобто
, тобто 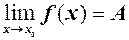 . Згідно означення 3 це значить, що для як завгодно малого
. Згідно означення 3 це значить, що для як завгодно малого 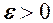 можна знайти число
можна знайти число 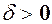 таке, що із нерівності
таке, що із нерівності 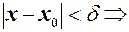 нерівність
нерівність 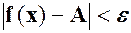 . Це означає, що для всіх
. Це означає, що для всіх 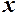 , що знаходяться від точки
, що знаходяться від точки 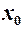 не дальше ніж на
не дальше ніж на 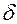 , відповідні точки
, відповідні точки  графіка функції
графіка функції  попадають в середину смуги шириною
попадають в середину смуги шириною 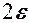 , обмежену прямими
, обмежену прямими 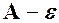 і
і 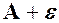 .
.
Можна довести, що означення 2 і 3 є еквівалентними.
Означення 2 зручно застосовувати для функцій, границя яких в даному процесі не існує. Розглянемо, наприклад, функцію  при
при 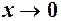 . Ця функція визначена для всіх значень
. Ця функція визначена для всіх значень 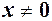 , є парною, її графік симетричний відносно осі
, є парною, її графік симетричний відносно осі  . Вияснимо поведінку функції
. Вияснимо поведінку функції  для конкретних трьох послідовностей
для конкретних трьох послідовностей 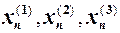 збіжних до
збіжних до 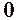 при
при  :
:
а) 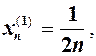 тоді
тоді 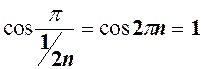 для
для 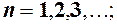
б) 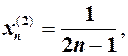 тоді
тоді  для
для 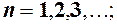
в) 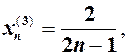 тоді
тоді  для
для  .
.
Отже, для наведених збіжних до нуля послідовностей функція  не прямує ні до якої границі, тобто
не прямує ні до якої границі, тобто
 не існує (див. частину графіка на рис. 22)
не існує (див. частину графіка на рис. 22)

Рис. 22
Графік функції  має вигляд нерівномірно стиснутої пружини: чим ближче до початку координат тим щільніше розміщуються окремі ланки пружини.
має вигляд нерівномірно стиснутої пружини: чим ближче до початку координат тим щільніше розміщуються окремі ланки пружини.
Означення 5. Число 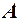 називається границею функції
називається границею функції  при
при  або
або 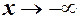 , якщо для як завгодно малого
, якщо для як завгодно малого 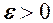 знайдеться число
знайдеться число 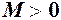 таке, що із нерівності
таке, що із нерівності 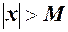 випливає нерівність
випливає нерівність 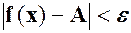 , при цьому пишуть
, при цьому пишуть
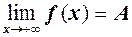 , або
, або 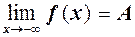 , або
, або 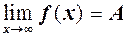 .
.
Таким чином співвідношення
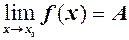
залишається правильним і в тому випадку, коли  або
або  .
.
3.4. Властивості границь
Теорема 1. Якщо функцію  при
при 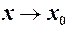 можна представити у вигляді суми сталої
можна представити у вигляді суми сталої 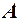 і нескінченно малої
і нескінченно малої  , тобто
, тобто
 , (1)
, (1)
то
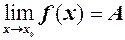 (
(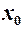 – скінченне або
– скінченне або 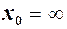 ). (2)
). (2)
Навпаки, якщо 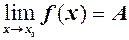 , то можна записати
, то можна записати
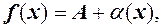 де
де 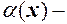 н.м. при
н.м. при 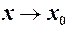 .
.
Дійсно, нехай 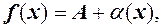 тоді
тоді 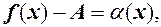 де
де 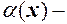 н.м. при
н.м. при 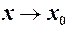 , тобто для
, тобто для 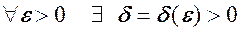 таке, що із нерівності
таке, що із нерівності 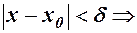 нерівність
нерівність  , або
, або 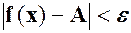 , а це і значить, що має місце рівність (2).
, а це і значить, що має місце рівність (2).
Навпаки, нехай виконується рівність (2). А це означає, що для  таке, що із
таке, що із 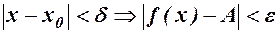 Позначимо
Позначимо 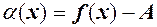 , тоді остання нерівність означає, що
, тоді остання нерівність означає, що
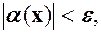 тобто н.м.
тобто н.м.
Наслідок. Якщо 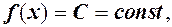 то
то 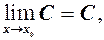 тобто границя сталої величини дорівнює цій сталій.
тобто границя сталої величини дорівнює цій сталій.
Дійсно, за теоремою 1 маємо 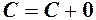 або
або 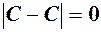 буде меншою
буде меншою 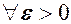 .
.
Теорема 2. Нехай існують скінченні границі 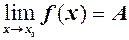 і
і 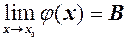 .Тоді
.Тоді  ,
, 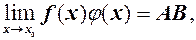
 за умови, що
за умови, що 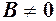 .
.
Доведемо, наприклад, другу рівність. За теоремою 1(формула 1) з того, що 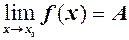 і
і 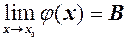 маємо:
маємо: 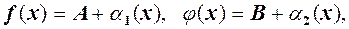 де
де 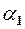 і
і 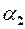 – н.м. при
– н.м. при 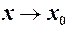 . Розглянемо добуток
. Розглянемо добуток 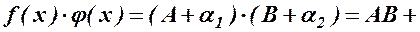 н.м. За теоремою 1 маємо, що число
н.м. За теоремою 1 маємо, що число 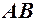 є границею функції
є границею функції 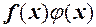 при
при 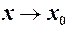 , тобто
, тобто 
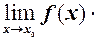
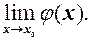
Рівності перша і третя теореми 2 доводяться аналогічно.
Наслідок. Сталий множник можна виносити за знак границі, тобто якщо  то
то
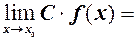
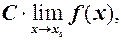
оскільки 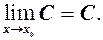
Означення 1. Функція  називається обмеженою при
називається обмеженою при 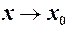 , якщо існує окіл з центром в точці
, якщо існує окіл з центром в точці 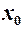 , в якому функція
, в якому функція  обмежена.
обмежена.
Означення 2. Функція  називається обмеженою при
називається обмеженою при  , якщо існує число
, якщо існує число 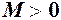 таке, що для всіх
таке, що для всіх 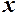 , які задовольняють нерівності
, які задовольняють нерівності 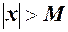 , функція
, функція  обмежена.
обмежена.
Теорема 3. Якщо границя  є скінченною, то функція
є скінченною, то функція 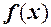 обмежена при
обмежена при 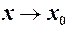 .
.
Доведення дамо, коли 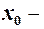 скінченне. Із рівності
скінченне. Із рівності  випливає, що для
випливає, що для 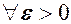 існує
існує 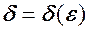 таке, що із
таке, що із 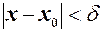 випливає
випливає 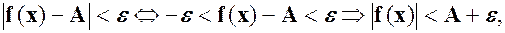 тобто
тобто 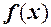 обмежена.
обмежена.
3.5. Теореми про існування границь
Теорема 1. Нехай при 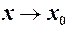 (
(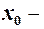 скінченне або
скінченне або 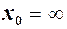 ) для трьох функцій виконується нерівність
) для трьох функцій виконується нерівність
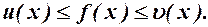
Якщо існують границі 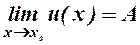 і
і  , які дорівнюють числу
, які дорівнюють числу 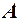 , то існує
, то існує
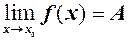 .
.
Доведення. Очевидно, що із нерівності 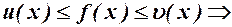

За теоремою 1 із 2.4. 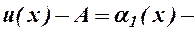 н.м.,
н.м., 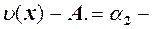 н.м. при
н.м. при 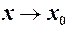 . Це значить, що для довільного
. Це значить, що для довільного 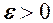 можна знайти
можна знайти 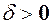 таке, що з нерівності
таке, що з нерівності 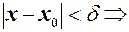
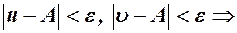
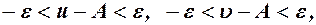 а, отже,
а, отже, 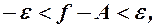 тобто
тобто 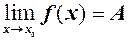 .
.
Теорема 2. Якщо функція 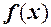 зростає, і якщо вона обмежена зверху, тобто
зростає, і якщо вона обмежена зверху, тобто  ,
, 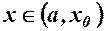 то ця функція має границю
то ця функція має границю 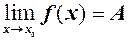 , де
, де 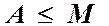 , а
, а  -скінчене або
-скінчене або 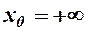 (див.рис.23).
(див.рис.23).
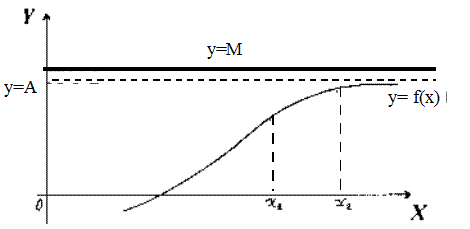
Рис. 23.
Аналогічне твердження має місце і для спадної, обмеженої знизу, функції 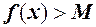 .
.
3.6. Односторонні границі
Будемо розглядати процес, коли змінна 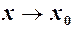 , але при цьому
, але при цьому 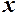 залишається меншим
залишається меншим 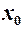 , тобто зліва. Цей факт позначають
, тобто зліва. Цей факт позначають 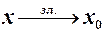 (зл. – зліва), або зручніше записувати
(зл. – зліва), або зручніше записувати 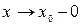 . Аналогічно, якщо
. Аналогічно, якщо 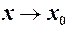 і
і 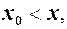 то будемо говорити, що
то будемо говорити, що 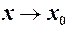 справа, позначають
справа, позначають 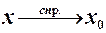 або
або  .
.
Означення. Число 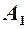 називається лівою границею функції
називається лівою границею функції 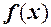 в точці
в точці 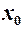 , якщо вона визначена на деякому напівінтервалі
, якщо вона визначена на деякому напівінтервалі  і для неї існує
і для неї існує 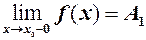 .
.
Аналогічно, якщо 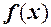 визначена в напівінтервалі
визначена в напівінтервалі  і існує
і існує  , то
, то 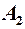 називається правою границею функції
називається правою границею функції 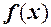 .
.
Ліва – і права границі називають односторонніми. Їх ще прийнято позначати
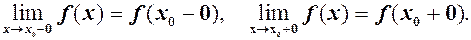
Зауваження. Рівності
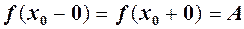
еквівалентні 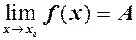 , тобто якщо односторонні границі існують і рівні в точці
, тобто якщо односторонні границі існують і рівні в точці 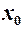 , то існує границя функції
, то існує границя функції 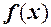 .
.
Якщо ж односторонні границі різні, тобто
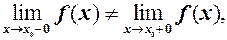
або хоча б одна з них не існує, тоді не існує й границя функції 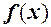 при
при 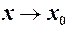 .
.
3.7. Невизначеності. Приклади знаходження деяких границь
При знаходженні границі ми використовуємо їх властивості, зокрема теорему 2 із 3.4. Можуть виникати такі випадки.
1. Якщо функція визначена в точці  , то
, то
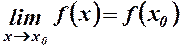 ,
,
тобто границя функції збігається з її значенням в точці 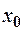 .
.
2. Якщо ж функція в точці 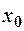 невизначена або
невизначена або 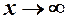 , то можуть зустрітись співвідношення вигляду:
, то можуть зустрітись співвідношення вигляду: 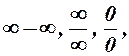
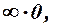
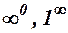 , які називаються невизначеностями.
, які називаються невизначеностями.
В більшості таких прикладів для знаходження границі над функціями, що стоять під знаком  необхідно виконати певні тотожні перетворення, або ще говорять: “позбавитися невизначеності” або “розкрити невизначеність”. А там, де невизначеності не зустрічаються, розв’язання здійснюються у відповідності теореми 2 та властивостей.
необхідно виконати певні тотожні перетворення, або ще говорять: “позбавитися невизначеності” або “розкрити невизначеність”. А там, де невизначеності не зустрічаються, розв’язання здійснюються у відповідності теореми 2 та властивостей.
 Розглянемо кілька конкретних прикладів з поясненнями
Розглянемо кілька конкретних прикладів з поясненнями
1) 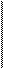 Знайти
Знайти 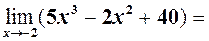 згідно теореми 2, а також =
згідно теореми 2, а також =
за наслідками із 2.4
= 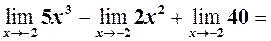

тобто границя функції збігається з її значенням, бо 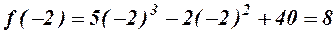 .
.
| 2) | 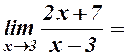
| Оскільки функція в точці 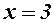 невизначена, і невизначена, і 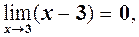 то теорему 2 не можна застосовувати. Робимо перетворення. то теорему 2 не можна застосовувати. Робимо перетворення.
| = |
| = | 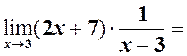
| Ф-я 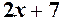 – обмежена – обмежена
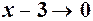 – н.м., оберненна – н.м., оберненна
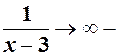 н.в., добуток їх – н.в. н.в., добуток їх – н.в.
|
= 
|
.
| 3) | 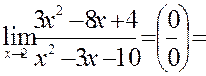
| В точці  ф. невизначена ф. невизначена
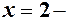 корінь чисельника і знаменника. Розклад на множники корінь чисельника і знаменника. Розклад на множники
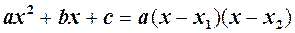
| = |
| = | 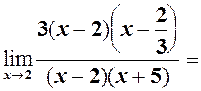
| оскільки 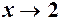 і, і, 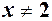 то на
то на 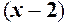 скорочуємо скорочуємо
| = 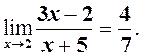
|
Зауваження. У загальному випадку, якщо
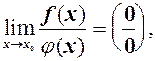 то необхідно зробити тотожні перетворення так, щоб
то необхідно зробити тотожні перетворення так, щоб 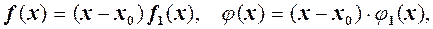 і тоді замість
і тоді замість
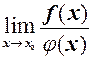 розглянути
розглянути 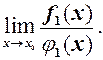
Це, зокрема, стосується випадку, коли 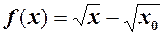 , тоді за допомогою тотожності
, тоді за допомогою тотожності
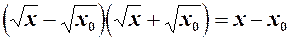 (1)
(1)
отримаємо
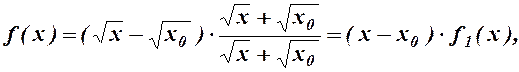
де 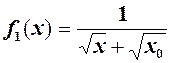 .
.
Аналогічно для 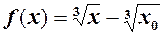 береться тотожність
береться тотожність
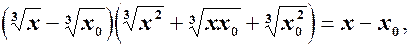 (2)
(2)
тоді
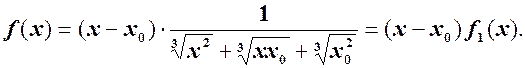
4) 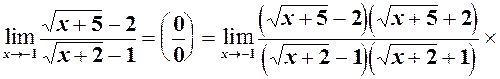
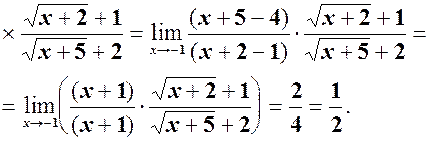
5) 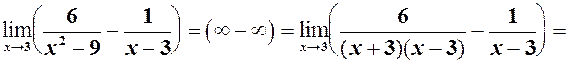


 6)
6)  див. формулу (2) =
див. формулу (2) =

3.8. Границя дробово раціональної функції при х ®¥
Розглянемо спочатку наступний приклад
7) 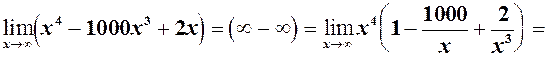
= (добуток н.в. на обмежену є н.в.) = ¥.
З даного прикладу можна зробити висновок, що у випадку многочлена із степенями різних знаків при  може бути невизначеність
може бути невизначеність 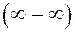 . Щоб її розкрити необхідно винести старший степінь за дужки. Враховуючи цей висновок, розглянемо границю дробово раціональної функції (див. 1.9) при
. Щоб її розкрити необхідно винести старший степінь за дужки. Враховуючи цей висновок, розглянемо границю дробово раціональної функції (див. 1.9) при  .
.
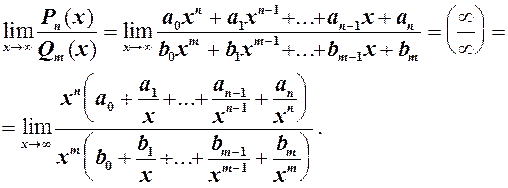
В кожній з дужок обмежені величини. Можливі три випадки:
1)  , тоді степені скорочуються і границя дорівнює відношенню коефіцієнтів при старших степенях
, тоді степені скорочуються і границя дорівнює відношенню коефіцієнтів при старших степенях  ;
;
2) 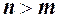 , тоді після скорочення в чисельнику залишиться
, тоді після скорочення в чисельнику залишиться 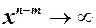 , тому границя дорівнює ¥;
, тому границя дорівнює ¥;
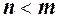 , тоді після скорочення в знаменнику залишиться
, тоді після скорочення в знаменнику залишиться 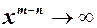 , а обернена до неї
, а обернена до неї 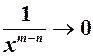 при
при  , в границі отримаємо
, в границі отримаємо 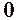 . Отже
. Отже
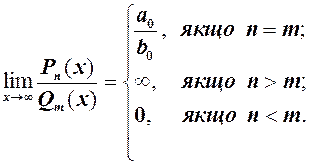 (1)
(1)
Приклади для самостійного розв’язання
Знайти границі.
1. 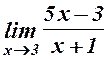 . 2.
. 2.  . 3.
. 3. 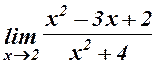 .
.
4. 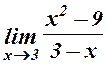 . 5.
. 5. 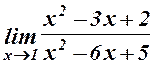 . 6.
. 6. 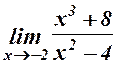 .
.
7.  . 8.
. 8. 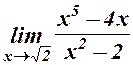 . 9.
. 9.  .
.
10. 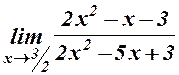 . 11.
. 11.  .
.
12.  . 13.
. 13. 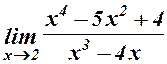 . 14.
. 14. 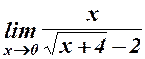 .
.
15. 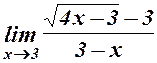 . 16.
. 16. 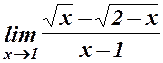 . 17.
. 17. 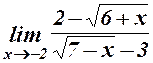 .
.
18. 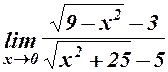 . 19.
. 19. 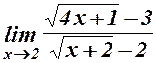 . 20.
. 20. 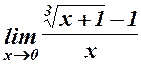 .
.
21. 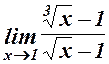 . 22.
. 22.  . 23.
. 23.  .
.
24. 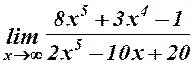 . 25.
. 25. 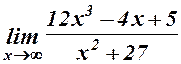 .
.
26. 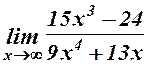 . 27.
. 27. 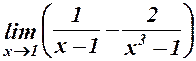 .
.
28. 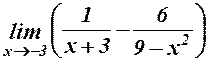 . 29.
. 29. 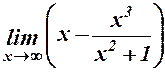 .
.
30. 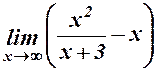 . 31.
. 31. 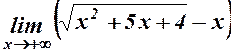 .
.
32. 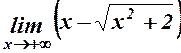 . 33.
. 33.  .
.
34. 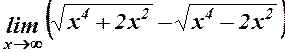 .
.
Відповіді. 1. 3. 2. 1. 3. 0. 4. -6. 5. 1/4. 6. -3. 7. 3/2. 8. 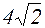 . 9.
. 9. 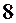 . 10.
. 10. 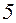 . 11.
. 11. 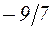 . 12.
. 12.  . 13.
. 13.  . 14.
. 14. 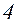 . 15.
. 15.  . 16.
. 16. 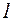 . 17.
. 17.  . 18.
. 18. 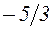 . 19.
. 19.  . 20.
. 20. 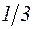 . 21. 2/3. 22.
. 21. 2/3. 22. 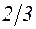 . 23.
. 23. 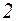 . 24.
. 24. 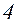 . 25.
. 25.  .
.
26. 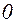 . 27. 1/2. 28.
. 27. 1/2. 28.  . 29.
. 29. 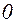 . 30. -3. 31.
. 30. -3. 31. 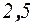 . 32.
. 32. 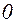 . 33.
. 33. 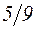 . 34.
. 34. 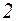 .
.
Перша важлива границя
Першою важливою називається границя
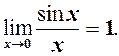 (1)
(1)
Для доведення (1) будемо виходити із геометричних міркувань (див. рис. 24)
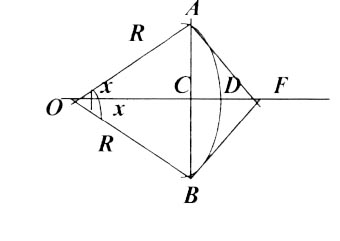
Рис. 24
Оскільки 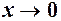 , то вважаємо, що кут 2
, то вважаємо, що кут 2  –гострий центральний кут в колі радіуса
–гострий центральний кут в колі радіуса  . Довжина хорди
. Довжина хорди 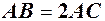 очевидно менша довжини дуги
очевидно менша довжини дуги 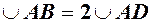 , а дуга
, а дуга 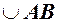 очевидно менша довжини ламаної
очевидно менша довжини ламаної 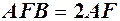 , тобто
, тобто
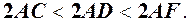
Із 
 . Довжина дуги
. Довжина дуги 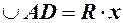 . Із
. Із 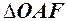 довжина дотичної
довжина дотичної 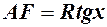 . Отже, нерівність запишеться
. Отже, нерівність запишеться
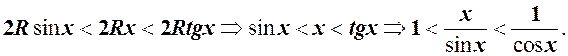
За теоремою 1 із 2.5 про границю нерівностей маємо
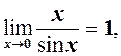
що рівносильно (1).
На основі (1) отримаємо ще кілька необхідних формул.
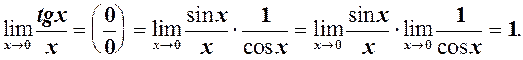
 . (2)
. (2)
 |  |
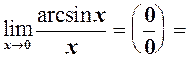 заміна
заміна 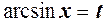
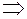
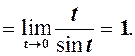
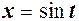 . Якщо
. Якщо
 то
то 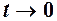
 (3)
(3)
Аналогічно
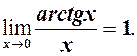 (4)
(4)
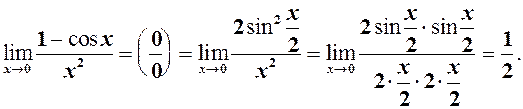
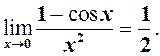 (5)
(5)
Приклади.
1. 

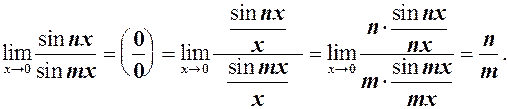
2.  Заміна
Заміна 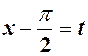 =
=

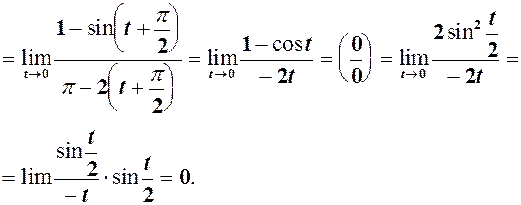
3. 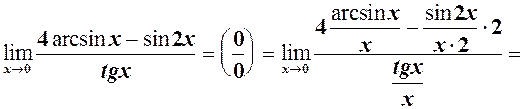
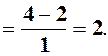
Приклади для самостійного розв’язання
Знайти границі
1. 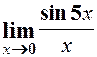 . 2.
. 2. 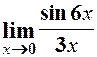 . 3.
. 3. 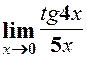 .
.
4. 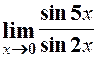 . 5.
. 5.  . 6.
. 6. 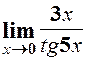 .
.
7. 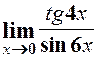 . 8.
. 8. 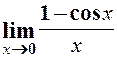 . 9.
. 9.  .
.
10. 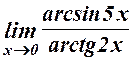 . 11.
. 11. 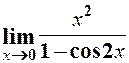 . 12.
. 12. 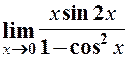 .
.
13. 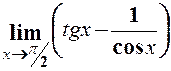 . 14.
. 14.  . 15.
. 15.  .
.
16. 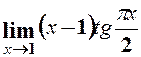 . 17.
. 17. 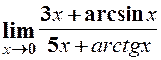 .
.
18.  . 19.
. 19. 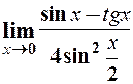 .
.
20. 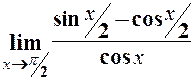 .
.
Відповіді. 1. 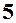 . 2.
. 2. 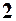 . 3.
. 3. 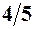 . 4.
. 4. 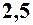 . 5.
. 5. 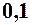 . 6.
. 6. 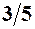 . 7.
. 7.  . 8.
. 8. 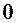 .
.
9. 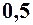 . 10.
. 10. 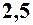 . 11.
. 11. 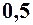 . 12.
. 12. 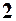 . 13.
. 13. 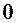 . 14.
. 14. 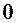 . 15.
. 15.  . 16.
. 16.  .
.
17.  . 18.
. 18. 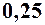 . 19.
. 19. 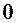 . 20.
. 20. 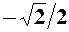 .
.
3.10. Натуральні логарифми. Границя, пов’язана з натуральним логарифмом
Розглянемо функцію 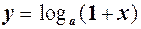 при
при  . Її область визначення:
. Її область визначення:  . Оскільки
. Оскільки  , то функція зростає. При
, то функція зростає. При 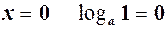 , графік проходить через початок координат (див. рис. 25)
, графік проходить через початок координат (див. рис. 25)
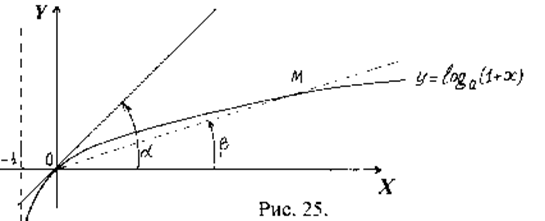
Нехай 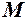 довільна точка графіка. Пряму
довільна точка графіка. Пряму  , що перетинає графік в двох точках
, що перетинає графік в двох точках 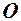 і
і 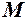 , називають січною. Січна
, називають січною. Січна  утворює з віссю
утворює з віссю  кут
кут 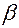 .
.
Припустимо, що точка 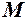 по кривій наближається до точки
по кривій наближається до точки 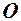 , тобто
, тобто 
 . Січна
. Січна  при цьому буде повертатись навколо точки
при цьому буде повертатись навколо точки 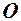 , кут
, кут 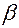 буде змінюватись. Точка
буде змінюватись. Точка  на кривій може вибиратись як справа, так і зліва відносно точки
на кривій може вибиратись як справа, так і зліва відносно точки  .
.
Означення. Граничне положення січної  , що проходить через точку
, що проходить через точку  , при умові що точка
, при умові що точка  кривої прямує до точки
кривої прямує до точки 
 називається дотичною до кривої
називається дотичною до кривої 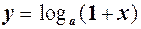 в точці
в точці 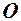 .
.
Позначимо через 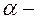 кут нахилу дотичної, тоді згідно означення маємо
кут нахилу дотичної, тоді згідно означення маємо
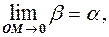 або
або 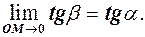 (1)
(1)
Тепер звернемо увагу на положення графіка 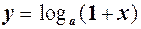 в залежності від основи
в залежності від основи  . Для прикладу розглянемо функції
. Для прикладу розглянемо функції
 При
При  маємо
маємо 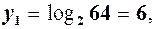
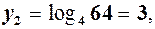
 Схематично положення кривих
Схематично положення кривих  зображено на рис. 26
зображено на рис. 26
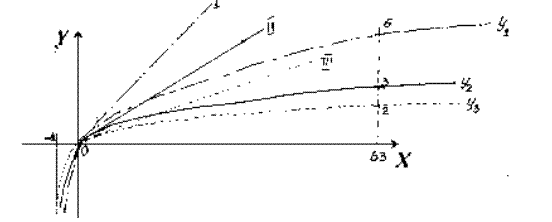
Рис.26
В точці  проведені відповідні дотичні: I, ІІ, ІІІ. Із рис. 26 зрозуміло, що при збільшені основи
проведені відповідні дотичні: I, ІІ, ІІІ. Із рис. 26 зрозуміло, що при збільшені основи  кут нахилу дотичної до
кут нахилу дотичної до 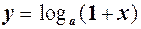 зменшується, а при зменшені
зменшується, а при зменшені  до
до 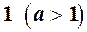 цей кут збільшується. Очевидно, що можна підібрати основу
цей кут збільшується. Очевидно, що можна підібрати основу  такою, щоб дотична до
такою, щоб дотична до 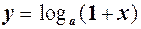 , що проходить через точку
, що проходить через точку 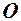 , утворювала з віссю
, утворювала з віссю  кут в
кут в 
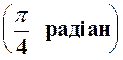 , тобто, щоб дотичною стала бісектриса
, тобто, щоб дотичною стала бісектриса  .
.
Можна довести, що значення шуканої основи 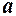 дорівнює ірраціональному числу
дорівнює ірраціональному числу 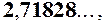 яке прийнято позначати буквою
яке прийнято позначати буквою  . Більш точно
. Більш точно  .
.
Число  було введено Л. Ейлером[1].
було введено Л. Ейлером[1].
Логарифми за основою  називаються натуральними, замість
називаються натуральними, замість
 пишуть
пишуть 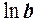 .
.
За формулою переходу до нової основи
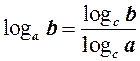
маємо зв’язок між десятковими та натуральними логарифмами
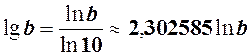 або
або 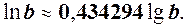
Має місце формула
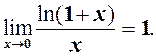 (2)
(2)
Дамо геометричне пояснення формули (2).
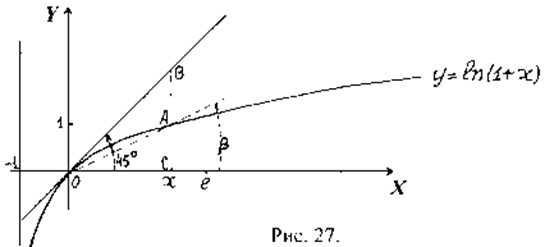
Згідно рис. 27 із 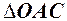 маємо
маємо
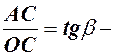 кутовий коефіцієнт січної, але
кутовий коефіцієнт січної, але 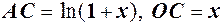 , тому
, тому
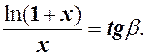
Якщо 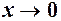 , то кут нахилу січної
, то кут нахилу січної 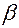 зростає до значення кута нахилу дотичної
зростає до значення кута нахилу дотичної 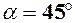 , тому у відповідності із співвідношенням (1)
, тому у відповідності із співвідношенням (1) 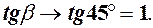 Звідки отримуємо (2).
Звідки отримуємо (2).
Дата публикования: 2015-11-01; Прочитано: 2215 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
