Теоретичний вступ

Інститут гуманітарних та соціальних наук

Кафедра “Соціальних комунікацій та інформаційної діяльності”

МЕТОДИЧНІ ВКАЗІВКИ

До лабораторної роботи №2

на тему „Алгоритм бектрекінг”

з курсу “Технології менеджменту знань”

для студентів, що навчаються за спеціальністю

8.18010015 „Консолідована інформація”

Львів - 2012

Мета лабораторної роботи полягає у вивченні алгоритму бектрекінг та застосування їх для розв’язування складних логічних задач.

Теоретичний вступ

Опишемо загальний метод, який дозволяє значно зменшити об’єм обчислень в алгоритмах типу „повного перебору всіх можливостей”. Щоб застосувати цей метод, розв’язок задачі повинен мати вигляд послідовності . Основна ідея методу полягає в тому, що розв’язок будується поступово, починаючи з порожньої послідовності (довжини 0), або з одноелементної послідовності (довжини 1). Взагалі, якщо маємо даний частковий (неповний) розв’язок , де , то намагаємось знайти таке допустиме значення , що не включається можливість продовження до повного розв’язку. Якщо таке допустиме, але ще не використане значення існує, то долучаємо цю нову компоненту до часткового розв’язку і продовжуємо процес для послідовності 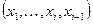. Якщо такого значення не існує, то повертаємось до попередньої послідовності 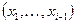і продовжуємо процес, шукаючи нове, ще не використане значення 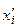- звідси назва „бектрекінг” (англ. backtracking – пошук з поверненням).

Роботу цього алгоритму можна інтерпретувати як процес обходу деякого дерева. Кожна вершина цього дерева природно відповідає деякій послідовності , причому вершини, які відповідають послідовностям виду , є синами цієї вершини. Корінь дерева відповідає порожній, а в деяких задачах одноелементній послідовності.

В алгоритмі бектрекінг здійснюється обхід цього дерева пошуком вглиб (для дерева це означає обхід зверху вниз). Крім того, задається предикат 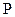, означений на всіх вершинах дерева. У випадку процес обходу відкидає розгляд вершин піддерева з коренем у вершині , зменшуючи тим самим обсяг перебору. Сам предикат 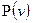набуває значення тоді, коли стає зрозумілим, що послідовність , яка відповідає вершині , ніяким способом не можна добудувати до повного розв’язку. Проілюструємо алгоритм бектрекінг на конкретних прикладах.

Приклад 1. Побудова гамільтонових циклів у графі. Починаємо у довільній вершині. Будуємо простий ланцюг доки це можливо. Якщо вдалося пройти всі вершини, то перевіряємо, чи існує ребро, яке з’єднує останню і початкову вершини цього ланцюга. Якщо описаний процес у певний момент неможливо продовжити, то повертаємось на одну вершину назад і намагаємося продовжити побудову ланцюга іншим способом.

Рис. 1

Пошук всіх гамільтонових шляхів у графі з п’ятьма вершинами (рис.1) ілюструється за допомогою дерева, зображеного на рис. 2. Розв’язки задачі обведені і до них у прямокутних рамках приписані відповідні гамільтонові цикли.

Рис. 2

Отже, замість побудови і аналізу 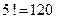послідовностей довжини 5 вершин графа з рис.1 ми розглянули всього 23 послідовності довжини від 1 до 5.

Приклад 2. Визначити, чи можна розфарбувати граф у 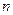кольорів. Спочатку фарбуємо вершину 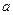у колір 1. Після цього фарбуємо вершину 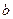у колір 1, якщо 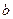не суміжна з вершиною 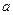. Інакше фарбуємо 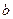у колір 2. Далі переходимо до третьої вершини . Використовуємо колір 1, якщо це можливо, для вершини . Інакше використовуємо колір 2, якщо це можливо. Тільки якщо жоден з кольорів 1 та 2 не може бути використаний, використовуємо колір 3. Продовжуємо цей процес доки це можливо, використовуючи один з n кольорів для кожної нової вершини, причому завжди використовуємо перший можливий колір зі списку кольорів. Якщо досягнемо вершину, яку не можна зафарбувати у жоден з n кольорів, то повертаємося до останньої зафарбованої вершини, відміняємо її колір і присвоюємо наступний можливий колір зі списку. Якщо і це неможливо, то повертаємось ще до попередньої вершини, відміняємо її колір і намагаємося присвоїти новий колір, наступний можливий зі списку. Цей процес продовжуємо аналогічним чином. Якщо розфарбування в n кольорів існує, то ця процедура знаходить таке розфарбування. На рис.3 зображено граф та процес присвоювання кольорів вершинам з використанням алгоритму бектрекінг (3 кольори).

Рис. 3

Приклад 3. Задача про 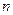ферзів. Як 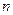ферзів можна розмістити на дошці 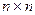так, щоб жодні два не били один одного? Для розв’язування цієї задачі потрібно визначити 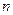позицій на дошці 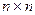так, щоб жодні дві позиції не були в одному рядку, в одному стовпчику і в одній діагоналі. Діагональ містить всі позиції 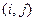такі, що 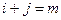для деяког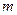о , або . Починаємо з порожньої дошки. На -му кроці намагаємось поставити нового ферзя в -му стовпчику, причому у перших стовпчиках вже є ферзі. Перевіряємо клітки у -му стовпчику, починаючи з першої. А саме, шукаємо таку позицію для ферзя, щоб він не був у рядку і діагоналі з тими ферзями, які вже є на дошці.

Якщо це неможливо, то повертаємось до місця ферзя на попередньому -му кроці і розміщаємо цього ферзя на наступному можливому рядку в цьому -му стовпчику, якщо такий рядок є. Якщо немає, то повертаємось до ферзя у -му стовпчику

Рис. 4

. Процес бектрекінг для проілюстровано на рис.4.

Рис. 4

Приклад 4. Суми елементів підмножин. Задана множина натуральних чисел 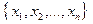. Знайти підмножину цієї множини таку, що сума її елементів дорівнює даному числу .

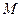Розв’язок. Починаємо з порожньої множини. Будуємо суму, послідовно добираючи доданки. Число із заданої послідовності включається в суму, якщо сума після додавання цього числа не перевищить 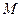. Якщо сума настільки велика, що додавання будь-якого нового числа перевищить 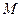, то повертаємось і міняємо останній доданок у сумі. На рис.5 зображено бектрекінг для задачі знаходження підмножини із сумою 39.

Рис. 5