Непрерывные Дроби

Последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную) дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби. Например, последовательность 1, 1/2, 2/3, 3/4,..., n/(n + 1),... порождает непрерывную дробь

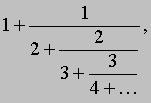<="" div="" style="font-size: 12px; font-family: Arial;">где многоточие в конце указывает на то, что процесс продолжается бесконечно. В свою очередь непрерывная дробь порождает другую последовательность дробей, называемых подходящими. В нашем примере первая, вторая, третья и четвертая подходящие дроби равны

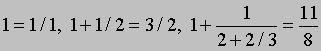<="" div="" style="font-size: 12px; font-family: Arial;">и

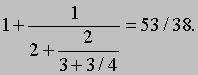<="" div="" style="font-size: 12px; font-family: Arial;">Их можно построить по простому правилу из последовательности неполных частных 1, 1/2, 2/3, 3/4,.... Прежде всего выпишем первую и вторую подходящие дроби 1/1 и 3/2. Третья подходящая дробь равна (2*1 + 3*3)/(2*1 + 3*2) или 11/8, ее числитель равен сумме произведений числителей первой и второй подходящих дробей, умноженных соответственно на числитель и знаменатель третьего неполного частного, а знаменатель равен сумме произведений знаменателей первого и второго неполных частных, умноженных соответственно на числитель и знаменатель третьего неполного частного. Четвертая подходящая дробь получается аналогично из четвертого неполного частного 3/4 и второй и третьей подходящих дробей: (3*3 + 4*11)/(3*2 + 4*8) или 53/38. Следуя этому правилу, находим первые семь подходящих дробей: 1/1, 3/2, 11/8, 53/38, 309/222, 2119/1522 и 16687/11986. Запишем их в виде десятичных дробей (с шестью знаками после запятой): 1,000000; 1,500000; 1,375000; 1,397368; 1,391892; 1,392247 и 1,392208. Значением нашей непрерывной дроби будет число x, первые цифры которого 1,3922. Подходящие дроби являются лучшим приближением числа x. Причем они поочередно оказываются то меньше, то больше числа x (нечетные - больше x, а четные - меньше). Чтобы представить отношение двух положительных целых чисел в виде конечной непрерывной дроби, нужно воспользоваться методом нахождения наибольшего общего делителя. Например, возьмем отношение 50/11. Так как 50 = 4Ч11 + 6 или 11/50 = 1/(4 + 6/11), и, аналогично, 6/11 = 1/(1 + 5/6) или 5/6 = 1/(1 + 1/5), получаем:

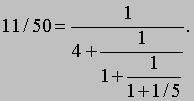<="" div="" style="font-size: 12px; font-family: Arial;">Непрерывные дроби используются для приближения иррациональных чисел рациональными. Предположим, что x - иррациональное число (т.е. непредставимо в виде отношения двух целых чисел). Тогда, если n0 - наибольшее целое число, которое меньше x, то x = n0 + (x - n0), где x - n0 - положительное число меньше 1, поэтому обратное ему число x1 больше 1 и x = n0 + 1/x1. Если n1 - наибольшее целое число, которое меньше x1, то x1 = n1 + (x1 - n1), где x1 - n1 - положительное число, которое меньше 1, поэтому обратное ему число x2 больше 1, и x1 = n1 + 1/x2. Если n2 - наибольшее целое число, которое меньше x2, то x2 = n2 + 1/x3, где x3 больше 1, и т.д. В результате мы шаг за шагом находим последовательность неполных частных n0, 1/n1, 1/n2,... непрерывной дроби, являющихся приближениями x. Поясним сказанное на примере. Предположим, что

">

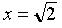
тогда

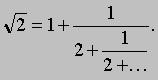
Первые 6 подходящих дробей равны 1/1, 3/2, 7/5, 17/12, 41/29, 99/70. Записанные в виде десятичных дробей они дают следующие приближенные значения

: 1,000; 1,500; 1,400; 1,417; 1,4137; 1,41428. Непрерывная дробь для

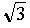
имеет неполные частные 1, 1/1, 1/2, 1/1, 1/2, 1/1,.... Иррациональное число является корнем квадратного уравнения с целочисленными коэффициентами в том и только в том случае, если неполные частные его разложения в непрерывную дробь периодичны. Непрерывные дроби тесно связны со многими разделами математики, например с теорией функций, расходящимися рядами, проблемой моментов, дифференциальными уравнениями и бесконечными матрицами. Если x - радианная мера острого угла, то тангенс угла x равен значению непрерывной дроби с неполными частными 0, x/1, -x2/3, -x2/7, -x2/9,..., а если x - положительное число, то натуральный логарифм от 1 + x равен значению непрерывной дроби с неполными частными 0, x/1, 12x/2, 12x/3, 22x/4, 22x/5, 32x/6,.... Формальным решением дифференциального уравнения x2dy/dx + y = 1 + x в виде степенного ряда является расходящийся степенной ряд 1 + x - 1!x2 + 2!x3 - 3!x4 +.... Этот степенной ряд можно преобразовать в непрерывную дробь с неполными частными 1, x/1, x/1, 2x/1, 2x/1, 3x/1, 3x/1,..., а ее в свою очередь использовать для получения решения дифференциального уравнения x2dy/dx + y = 1 + x.

Правила знаков

Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.

Рассмотрим подробней основные правила знаков.

Деление.

Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».

Умножение.

Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».