 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Кольцо классов вычетов по модулю m
|
|
Определение 13.  Пусть ℤ m - множество всех классов вычетов по модулю m. Определим операции «+» и «×» на множестве ℤ m по следующему правилу:
Пусть ℤ m - множество всех классов вычетов по модулю m. Определим операции «+» и «×» на множестве ℤ m по следующему правилу:
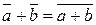 (1)
(1)
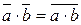 (2),
(2), 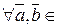 ℤ m.
ℤ m.
Пример:
ℤ 6 ={ 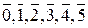 },
}, 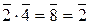 ,
, 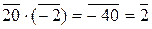 (используем Замечание 2).
(используем Замечание 2).
Лемма 1. Операции «+» и «×» на множестве ℤ m, заданные формулами (1), (2) определены корректно, т.е. результат операций не зависит от выбора представителей классов, т.е. если 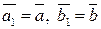 , то
, то 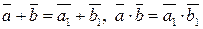 .
.
Доказательство:
Так как 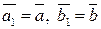 , то
, то 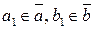 , и
, и 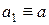 (mod m),
(mod m), 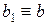 (mod m)
(mod m) 
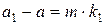 и
и 

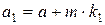 ,
, 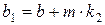 , то
, то 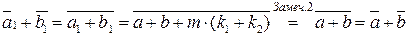
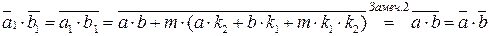 .
.
Теорема 14. Множество ℤ m всех классов вычетов по модулю m является ассоциативно-коммутативным кольцом с единицей, причем
1) если m- составное число, то ℤ m - кольцо с делителями 0.
2) если m = р- простое число, то ℤ m - поле характеристики р.
Доказательство: Проверим, что для ℤ m выполняются все условия определения кольца.
1) Операции «+» и «×», заданные формулами (1), (2) являются алгебраическими в силу определения 13.
а) Так как сложение и умножение классов вычетов сводится к сложению и умножению целых чисел, а на ℤ операция «+» и «×» ассоциативно-коммутативны и выполняются дистрибутивные законы, то на ℤ m операции ассоциативные, коммутативные и выполняются дистрибутивные законы.
б) 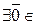 ℤ m, такой, что
ℤ m, такой, что 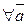
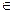 ℤ m:
ℤ m: 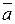 +
+ 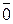 =
= 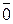 +
+ 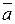 =
= 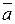
в) 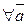
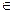 ℤ m,
ℤ m, 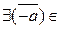 ℤ m, такой, что
ℤ m, такой, что 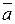 +
+ 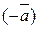 =
= 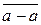 =
= 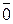
г) 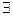
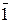
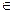 ℤ m, причем
ℤ m, причем 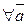
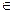
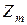 :
: 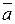 ×
× 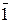 =
= 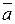
Таким образом,. ℤ m - ассоциативно-коммутативное кольцо с единицей.
2) 1. Пусть m – составное число, тогда m=m 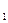 ×m
×m 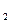 ,где 1 < mi<m, i= 1,2
,где 1 < mi<m, i= 1,2 
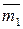
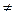
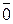 ,
, 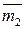
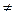
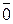 , причем
, причем 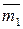 ⋅
⋅ 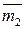 =
=  =
= 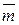 =
= 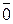
 ℤ m - кольцо с делителями нуля
ℤ m - кольцо с делителями нуля 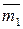 и
и 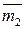 .
.
2. Пусть m=p – простое число. Покажем, что ⋅ ℤ p - поле.
Пусть 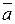
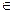 (ℤp)
(ℤp) 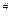 . Покажем что
. Покажем что 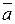 - обратим.
- обратим.
Так как 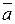
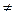
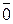 , то (a,p) = 1
, то (a,p) = 1 
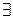 x,y Îℤ, такие что 1= a×x+p×y
x,y Îℤ, такие что 1= a×x+p×y 
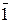 =
= 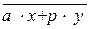

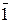 =
= 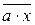 +
+ 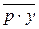

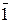 =
= 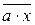

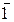 =
= 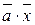

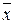 - элемент обратный для
- элемент обратный для 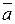
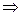 ℤp-поле.
ℤp-поле.
Покажем, что Char ℤp= p
а) покажем, что p × 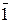 =
= 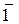 +
+ 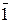 +…+
+…+ 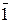 =
= 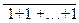 =
= 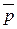 =
= 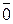 , т. е. p ×
, т. е. p × 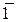 =
= 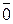 (*)
(*)
б) покажем, что p – наименьшее натуральное число удовлетворяющее (*)
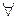 n
n 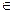 N, n<p:
N, n<p: 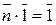

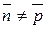 , т. е. p – наименьшее натуральное число удовлетворяющее (*).
, т. е. p – наименьшее натуральное число удовлетворяющее (*).
Из а), б)  Char ℤp = p.
Char ℤp = p.
Дата публикования: 2015-11-01; Прочитано: 3735 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
