 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства функций, непрерывных на отрезке
|
|
Функция 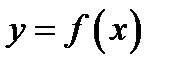 называется непрерывной на отрезке
называется непрерывной на отрезке 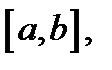 если а) она непрерывна в любой точке
если а) она непрерывна в любой точке  а на концах
а на концах 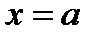 и
и 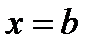 отрезка непрерывна справа и слева соответственно, т.е.
отрезка непрерывна справа и слева соответственно, т.е. 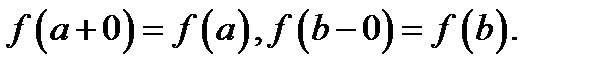 Функции, непрерывные на отрезке, обладают рядом замечательных свойств, сформулированных ниже.
Функции, непрерывные на отрезке, обладают рядом замечательных свойств, сформулированных ниже.
1. Теорема Вейерштрасса 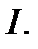 Если функция
Если функция  непрерывна на отрезке
непрерывна на отрезке 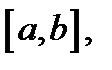 то она ограничена на этом отрезке, т.е. существует постоянная
то она ограничена на этом отрезке, т.е. существует постоянная 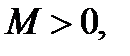 такая, что
такая, что 
2. Теорема Вейерштрасса  Если функция
Если функция  непрерывна на отрезке
непрерывна на отрезке 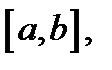 то она достигает на этом отрезке своих наибольшего и наименьшего значений, т.е. существуют точки
то она достигает на этом отрезке своих наибольшего и наименьшего значений, т.е. существуют точки 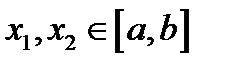 такие, что
такие, что 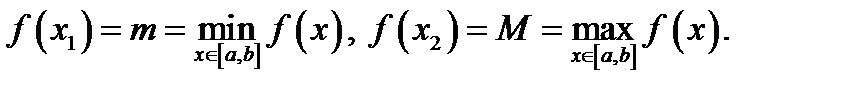
3. Теорема Больцано-Коши 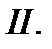 Если функция
Если функция  непрерывна на отрезке
непрерывна на отрезке 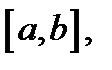 то каково бы ни было значение
то каково бы ни было значение 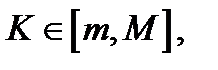 существует значение
существует значение 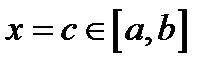 такое, что
такое, что 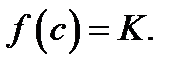
4. Теорема Больцано-Коши 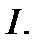 Если функция
Если функция  непрерывна на отрезке
непрерывна на отрезке 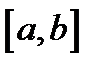 и принимает на концах этого отрезка значения разных знаков
и принимает на концах этого отрезка значения разных знаков 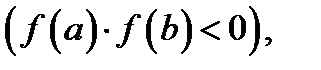 то существует хотя бы одно значение
то существует хотя бы одно значение 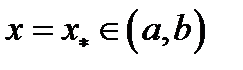 такое, что
такое, что 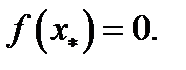
2. Монотонность функции
Напомним определение монотонных функций.
Определение 1. Говорят, что функция 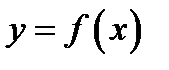 строго возрастает на множестве
строго возрастает на множестве 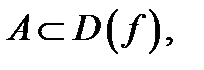 если для любых
если для любых 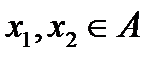 из неравенства
из неравенства 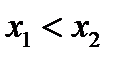 вытекает неравенство
вытекает неравенство 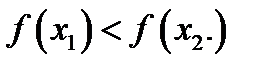 Если же
Если же 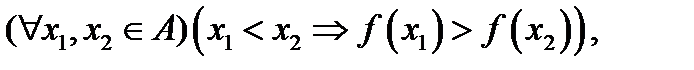 то функция
то функция 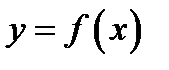 называется строго убывающей на множестве
называется строго убывающей на множестве 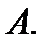 Если же из строгого неравенства
Если же из строгого неравенства 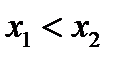 между аргументами вытекают нестрогое неравенство
между аргументами вытекают нестрогое неравенство 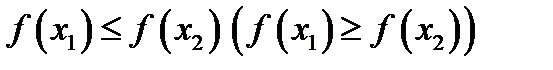 между значениями функции, то говорят, что
между значениями функции, то говорят, что 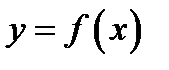 является неубывающей (соответственно невозрастающей) на множестве
является неубывающей (соответственно невозрастающей) на множестве 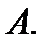 Множество всех функций строго возрастающих и строго убывающих образует класс строго монотонных функций; невозрастающие и неубывающие функции образует класс просто монотонных функций.
Множество всех функций строго возрастающих и строго убывающих образует класс строго монотонных функций; невозрастающие и неубывающие функции образует класс просто монотонных функций.
При исследовании на монотонность функций используются выписанная ранее
Теорема Лагранжа. Если функция 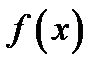 непрерывна на отрезке
непрерывна на отрезке 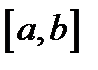 и является дифференцируемой по-крайней мере в интервале
и является дифференцируемой по-крайней мере в интервале 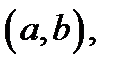 то существует точка
то существует точка 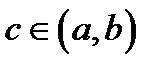 такая, что
такая, что
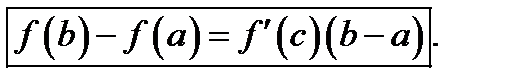
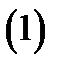
Теорема 1. Пусть функция 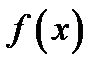 непрерывна на отрезке
непрерывна на отрезке 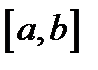 и является дифференцируемой по-крайней мере в интервале
и является дифференцируемой по-крайней мере в интервале 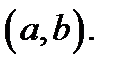 Тогда справедливы следующие высказывания:
Тогда справедливы следующие высказывания:
1. если 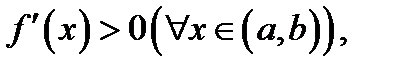 то функция
то функция 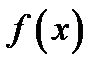 строго возрастает на отрезке
строго возрастает на отрезке 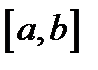 ;
;
2. если  то функция
то функция 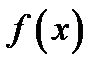 строго убывает на отрезке
строго убывает на отрезке 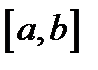 .
.
Доказательство вытекает из равенства (1), в котором надо положить 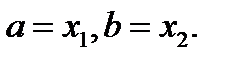 Действительно, если
Действительно, если  а
а 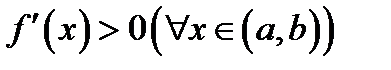 (тогда и
(тогда и 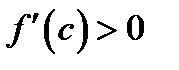 ), то (см. (1)) будет
), то (см. (1)) будет
выполняться неравенство  Это означает, что функция
Это означает, что функция 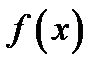 строго возрастает на отрезке
строго возрастает на отрезке 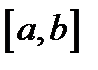 . Аналогично доказывается высказывание 2. Теорема доказана.
. Аналогично доказывается высказывание 2. Теорема доказана.
Замечание 1. Можно показать, что в случае нестрогого знака производной имеет место высказывание:
3. Для того чтобы функция  удовлетворяющая условиям теоремы 1, была неубывающей (невозрастающей) на отрезке
удовлетворяющая условиям теоремы 1, была неубывающей (невозрастающей) на отрезке 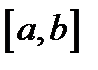 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 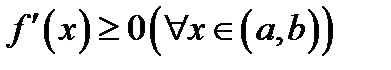 (соответственно
(соответственно 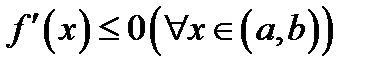 ).
).
Например, функция 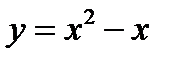 строго убывает на любом отрезке
строго убывает на любом отрезке 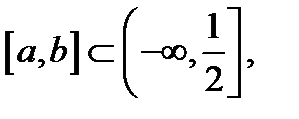 так как
так как 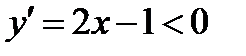 при
при 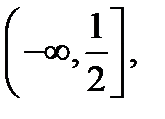 и эта функция строго возрастает на
и эта функция строго возрастает на 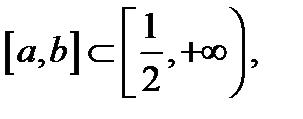 так как
так как 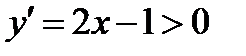 при
при 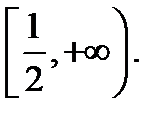
Дата публикования: 2015-11-01; Прочитано: 274 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
