Свойства и теоремы о векторах и координатах на плоскости

Мендель Виктор Васильевич

Применение векторов и координат для решения задач

Введение

Одним из универсальных приемов решения геометрических задач является метод координат. Кроме этого, часто (особенно при доказательстве различных неравенств) используется векторный метод.

Вы уже хорошо знакомы с векторами, координатами и их свойствами. Цель нашей работы: научиться применять знания для решения задач. Здесь большое значение имеет опыт: чем с большим числом приемов решений и доказательств вы ознакомились – тем “мощнее” ваш арсенал.

Дадим несколько общих указаний, которые помогут сориентироваться и решить, можно ли в данной задаче использовать векторы и координаты:

Во-первых, естественно, нужно применять координатный или векторный метод, если в условиях задачи говорится о векторах или координатах;

Во-вторых, координатный метод может помочь, если в задаче требуется определить геометрическое место точек (т.е. спрашивается, какую фигуру образуют точки, удовлетворяющие некоторому условию);

В-третьих, очень полезно применить координатный метод, если из условия задачи не понятно, как расположены те или иные точки;

В-третьих, полезно и удобно применять координаты и векторы для вычисления углов и расстояний;

В-четвертых, вообще, часто, когда не видно ни каких подходов к решению задачи, или вы не можете составить уравнения, попробуйте применить координатный метод. Он не обязательно даст решение, но поможет разобраться с условиями и даст толчок к поиску другого решения.

Вооружившись этими советами и повторив материал по школьному учебнику геометрии[1], вы можете двигаться дальше. В следующем параграфе изложен материал, который не включен в школьный учебник, но может быть весьма полезен нам в дальнейшем.

Свойства и теоремы о векторах и координатах на плоскости

п.1. Разные способы определения координат точки на плоскости

1.1. В математике используется два способа введения координат. В первом случае используются понятия: “систе­ма координат”, “координатные оси”, “координаты точки”. Тогда координаты точки определяются как координаты ее проекций на координатные оси (ОХ) и (OY). 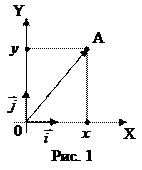Аналогично определяются и координаты вектора. Остановимся на этом по подробнее: В прямоугольной системе координат векторы 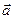, 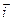и отложим от точки О – начала координат (см. Рис. 1). В этом случае координаты вектора 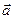совпадают с координатами точки А в рассматриваемой системе координат. Поэтому координаты вектора вычисляются как координаты его конца – точки А.

Во “взрослой” математике применяется другой способ определения координат точки. Познакомимся с ним. Рассмотрим вектор, начало которого находится в начале координат, а конец – в некоторой точке А. Вектор 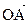называют радиус-вектором точки А. Коэффициенты разложения радиус-вектора по векторам и мы и будем называть координатами точки А.

Такое определение может показаться ненужным, с его помощью координаты построенной на чертеже точки не найдешь. Но оно позволяет применять аппарат векторной алгебры для работы с координатами точек. В этом читатель может убедиться, познакомившись с примерами.

Пример 1. Пусть нам даны координаты точек М₁ и М₂: М₁(х₁; у₁), М₂(х₂; у₂). Надо найти координаты точки М, такой, что 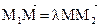(где λ – некоторое действительное число, не равное -1).

Решение: При изучении темы “Векторы” в 8 классе вы узнали, что для любой точки О и указанных выше точек М₁, М₂ и М имеет место векторное равенство:

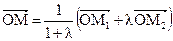(2.1)

Выберем точку О так, чтобы она совпала с началом координат. Тогда векторы 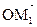, 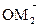и 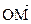и будут радиус-векторами точек М₁, М₂ и М и их координаты будут совпадать с координатами самих точек.

Применим к уравнению (2.1) известные правила действий над векторами в координатах. Мы получим для координат (х; у) вектора 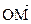следующие выражения:

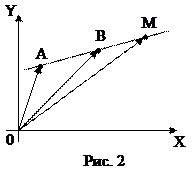
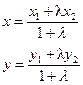(2.2)

Так как координаты радиус-вектора равны координатам точки, то формулы (2.2) дают нам искомое решение.

Следующий пример показывает, как можно задать координаты точек, лежащих на некоторой прямой.

Пример 2. Пусть нам известны координаты двух разных точек А и В (А(х₁; у₁), В(х₂; у₂)). Требуется выразить через них координаты (x, y) любой точки М, лежащей на прямой АВ.

Решение: Конечно, мы можем попробовать составить уравнение прямой так, как этому вас учат на уроках алгебры. Однако попробуем векторный метод. На рисунке 2 вы видите, что радиус-вектор точки М – вектор 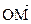по правилу треугольника можно представить в виде суммы 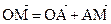. Обратим также внимание на то, что векторы 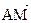и коллинеарны, и значит (по признаку коллинеарности) 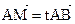, где t – некоторое число. Заметим также, что 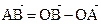, поэтому окончательно получим:

.

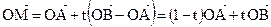Для координат (х; у) точки М имеем:

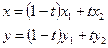(2.3)

Задача решена.

Замечание 1. В примере мы изначально считаем, что число t - любое. Если же ввести ограничение 0≤t≤1, то получатся координаты всех точек отрезка АВ.

Замечание 2. Уравнения (2.3) называют параметрическими уравнениями прямой (число t – параметр).

Параметрические уравнения прямой можно получить и по другому. Параметрические уравнения прямой, проходящей через точку М₀(х₀; у₀) и параллельной вектору 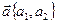имеют вид

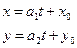(2.3’)

п.2. Длина вектора и отрезка

Напомним, что если вектор 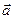имеет координаты (а₁; а₂), то его длина равна: 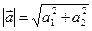(2.4)

Если известны координаты концов отрезка (А(х₁; у₁), В(х₂; у₂)), то его длина равна:

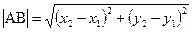(2.5)

Обратим внимание читателей еще на один интересный факт, связанный с координатами вектора единичной длины.

Пример 3. Найдите координаты единичного вектора 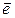, если он составляет с осью ОХ угол .

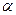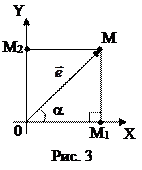Решение: Отложим единичный вектор от начала координат. Пусть .

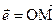Координаты точки М (а значит, и вектора 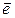) равны 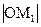и 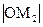, где М₁ и М₂ – проекции точки М на координатные оси. Рассмотрим прямоугольный треугольник ОМ₁М. Его прилежащий катет ОМ₁= 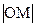×cosa. Заметим, что 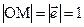по условию. Таким образом, 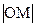=cosa. Теперь рассмотрим 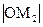: т.к. ОМ₁ММ₂ – прямоугольник, то .

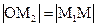С другой стороны, М₁М – противолежащий катет треугольника ОМ₁М, и его длина равна: 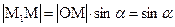. Отсюда и . Таким образом, координаты вектора 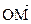такие: 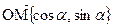(2.6)

Замечание: Мы рассмотрели случай, когда лежит в I-ом координатном угле. Другие случаи можно рассмотреть аналогично.

1.1. 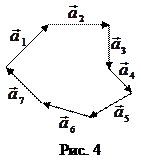Напомним, что для длин векторов выполняется неравенство треугольника: 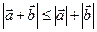(2.7)

Как следствие, длина суммы двух единичных векторов не больше двух, а длина суммы n единичных векторов не превосходит число n:

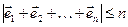, где все 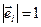(2.8)

п.3 Векторы и многоугольники

3.1. В некоторых задачах на векторы требуется выяснить, можно ли из данных векторов составить многоугольник. Поясним, что это означает: векторы откладываются так, что конец предыдущего является началом следующего. Если конец последнего вектора совпадет с началом первого, то “цепочка” замкнется и получится замкнутая ломаная. Это и означает, что из векторов можно построить многоугольник.

Алгебраически это означает, что сумма рассматриваемых векторов равна нулевому вектору: 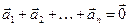(2.9)

Замечание: Иногда это условие заменяется другим: один из векторов равен сумме остальных, т.е. 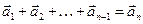(2.10)

п.4. Целочисленные решетки [2]

4.1. Иногда встречаются задачи, в которых рассматриваются точки, координаты которых – целые числа. Такие точки принято называть узлами и вот почему. Отметим на оси ОХ точки с целыми координатами и проведем через них прямые, параллельные оси ОY. Затем также поступим с аналогичными точками оси OY. В результате мы получим “решетку”, каждая “ячейка” которой – квадрат со стороной, равной единице. Точки с целыми координатами будут служить вершинами ячеек – узлами.

4.2. Если параллелограмм имеет целочисленные вершины, и одна из его сторон параллельна какой-нибудь координатной оси, то площадь параллелограмма – целое число.

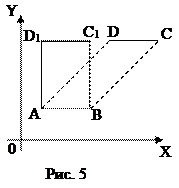Чтобы убедиться в этом, посмотрим на рисунок 5. Мы видим, что параллелограмм АВСD и прямоугольник АВС₁D₁ имеют общее основание АВ и равные высоты. Очевидно, что если координаты вершин прямоугольника – целые числа, то его длина и высота – также целые числа. Значит и площадь прямоугольника – целое число. С другой стороны, площадь параллелограмма равна площади прямоугольника. Значит она тоже целое число.

Замечание: Мы далее получим формулу, из которой следует, что у любого параллелограмма с целочисленными вершинами, площадь – целое число.

п.5. Скалярное произведение векторов

5.1. Скалярным произведением векторов 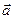и 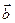называется число, равное произведению длин этих векторов на косинус угла между ними:

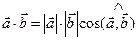(2.11)

5.2. Скалярное произведение в координатах находим по формуле:

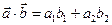(2.12)

здесь .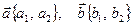

5.3. Если векторы перпендикулярны, то их скалярное произведение равно нулю.

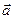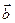^ Û ).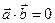

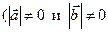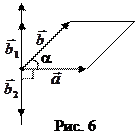5.4. Пример 4. Для вектора 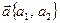найдите перпендикулярный, равный ему по длине.

Решение: Рассмотрим векторы 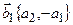и 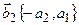. Очевидно, что 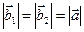(формула 2.4). Легко убедиться, что 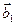^ 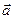. Действительно, 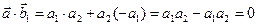Þ 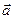^ 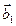. Аналогично показывается, что ^ .

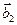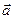Таким образом, 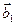и 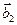– искомые векторы.

5.5. Угол между векторами вычисляется по формуле 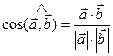(2.13)

В координатах эта формула имеет вид: 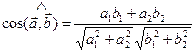(2.14)

5.6. Из определения синуса и косинуса угла в прямоугольном треугольнике следует, что для его острых углов a и b имеют места равенства 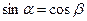и 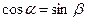. Так как b=90°-a (из свойств углов прямоугольного треугольника), то 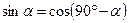и 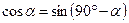. (2.15)

Найдем формулу для вычисления площади параллелограмма, построенного на векторах 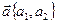и 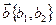. Воспользуемся известной формулой для вычисления площади параллелограмма: 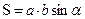(*). Из рисунка 6 видно, что 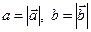и 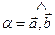. Поэтому по формуле (2.4) 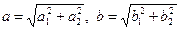. Нам теперь нужно найти sina. Поступим следующим образом. Рассмотрим векторы 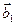и 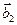из пункта (5.4). На чертеже 6 видно, что один из углов 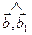, или 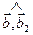равен 90°-a. (Какой именно, зависит от того, с какой стороны от 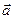лежит вектор 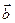. Есл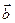и и 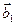лежат по одну сторону от 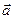, берем первый угол, если по разные стороны – второй).

Найдем 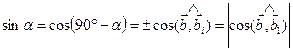. Используем формулы (2.14)

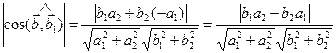
Подставим все найденные значения в формулу (*). Получим окончательное выражение для площади параллелограмма:

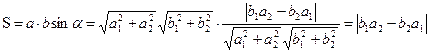
Итак 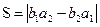(2.16)

п.6 Задание геометрического места точек аналитическим условием на их координаты.

6.1. Вы уже знаете, что некоторые геометрические фигуры можно задать уравнением. Например: прямая задается (в прямоугольной системе координат) уравнением y=kx+b, а окружность с центром в точке M₀(x₀, y₀) и радиусом R, задается уравнением: (x-x₀)²+(y-y₀)²=R².

С другой стороны, геометрическую фигуру можно задать как геометрическое место точек, например:

· множество точек, удаленных от данной точки на расстояние R (окружность),

· множество точек, равноудаленных от концов данного отрезка (серединный перпендикуляр к отрезку),

· множество точек, равноудаленных от сторон угла (прямая, содержащая биссектрису этого угла).

Ниже мы рассмотрим более сложные примеры геометрических мест точек.

Теперь подробнее остановимся на понятии “аналитическое условие”. Задать фигуру аналитическим условием, значит в некоторой системе координат найти уравнения или неравенства, которым удовлетворяют координаты точек этой фигуры.

Рассмотрим пример.

6.2. Пример 5.

Система неравенств 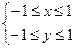задает на координатной плоскости квадрат, длины сторон которого равны двум, центр совпадает с началом координат, а стороны параллельны осям координат.

6.3. В геометрии можно рассматривать три основных задачи:

· отыскание аналитических условий для некоторого геометрического места точек,

· определение по аналитическим условиям вида и строения геометрического места точек (что собой представляет данное множество, какая это фигура –окружность, отрезок, луч и т.п.),

· использование аналитических условий для исследования геометрических свойств фигуры.

В рамках данной статьи мы ограничимся рассмотрением нескольких примеров нахождения аналитических условий.

§ 3. Примеры решения задач

3.1. Даны координаты вершин треугольника АВС: А(1, 0), В(4, -3), С(12, 5). Точки М и N лежат на сторонах АВ и ВС соответственно и делят их в одинаковом отношении 1:2. Найдите координаты середины отрезка MN.

Решение:

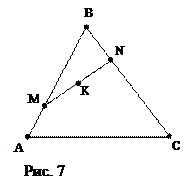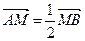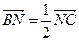Из чертежа (рис. 7) и условия задачи следует, что и . Найдем координаты точек М и N по формулам (2.2):

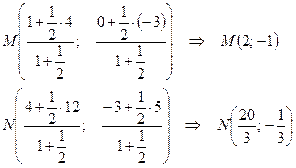
Теперь, зная координаты концов отрезка MN, найдем координаты его середины:

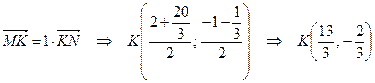
Ответ: .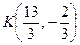

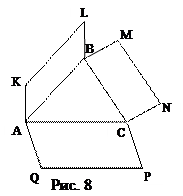
3.2. На сторонах треугольника АВС построены параллелограммы AKLB, BMNC и CPQA (рисунок 8). Можно ли составить треугольник из векторов 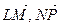и ?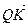

Решение:

Сумма векторов 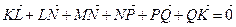, так как они образуют замкнутый контур. Так как 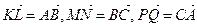и 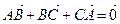, то из первого равенства получаем, что 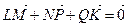. А из п. 3.1. следует, что эти векторы могут составить треугольник.

3.3. Не производя построение, определите, являются ли точки А (1, 2), В (6, -2), С (3, 4) и

D (-12, 0) вершинами выпуклого четырехугольника.

Решение:

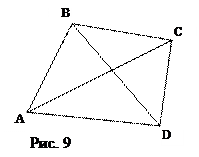Необходимым и достаточным условием того, что четырехугольник выпуклый, является то, что отрезки АС и BD – диагонали – пересекаются (рисунок 9). Составим параметрические уравнения отрезков АС и BD:

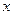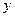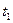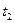Приравняем координаты и , тогда мы получим два уравнения относительно неизвестных и . Найдем их решения. Если выполнены условия 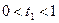и 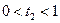, то точка пересечения прямых AC и BD лежит внутри обеих диагоналей, значит, диагонали пересекаются и четырехугольник – выпуклый. Если хотя бы одно условие нарушено, четырехугольник не выпуклый. Итак:

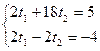
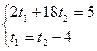
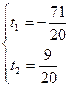
Мы видим, что t₁ не удовлетворяет условию 0<t₁<1, значит четырехугольник – невыпуклый.

3.4. В равнобедренном треугольнике ABC AC=2a, высота BH=h, BA=BC. На стороне AB лежит точка M (AM:MB=1:2), на стороне BC точка - N (BN:NC=2:3). На прямой MN лежит центр окружности, касающейся сторон внешнего угла треугольника при вершине C. Найдите радиус этой окружности.

Решение:

1. Из чертежа (рисунок 11) видно, что центр искомой окружности лежит на пересечении прямой MN и биссектрисы внешнего угла треугольника при вершине С.

2. Введем систему координат так: H – начало координат, HC – ось OX, HB – ось OY. Тогда координаты A(-a,0), B(0,h), C(a,0).

3. Используя формулы (2.2) деления отрезка в данном отношении, найдем координаты M(l₁=1/2) и координаты N(l₂=2/3):

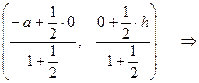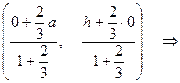M M N N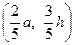

4. Найдем вектор, лежащий на биссектрисе CO: для этого от точки С отложим вектор 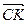, длина которого равна 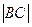. Тогда вектор 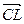= 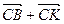лежит на биссектрисе CO (Подумайте, почему. Это вам пригодится при решении задачи № 3).

4.1. Найдем длину ВС: 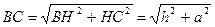. Поэтому координаты .

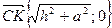4.2. Координаты 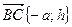, поэтому координаты .

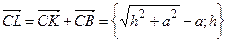5. Перпендикуляр, опущенный из точки О на прямую АС с одной стороны равен радиусу искомой окружности, а с другой стороны – координате 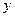точки О. Поэтому наша задача сводится к отысканию координаты 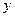точки пересечения прямых MN и СО.

5.1. Составим параметрические уравнения прямой MN (см. 2.3):

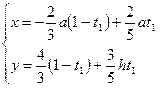
5.2. Найдем координаты точки L: Её радиус-вектор представляется как сумма 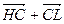, откуда .

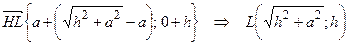5.3. Теперь составим уравнения прямой:

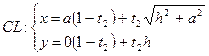
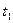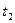Найдем, при каких и координаты точек прямых MN и CL совпадают, для этого в уравнениях этих прямых приравняем правые части:

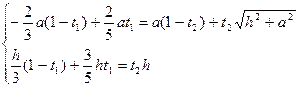
Умножим левую и правую части первого уравнения на 15, а во втором выразим 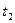через :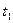

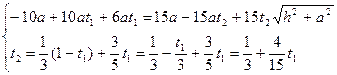
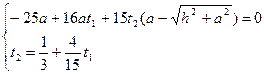
Выразим в первом уравнении 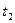через :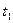

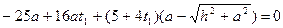
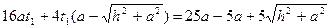
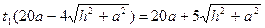
В принципе, мы можем найти значение 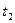, но нас оно не интересует. Теперь достаточно в уравнениях прямой (MN) найти координату у (это и есть искомый радиус):

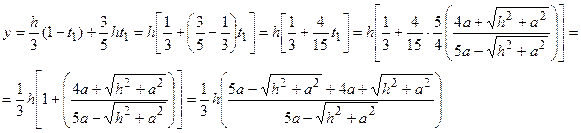
Отсюда .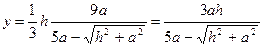

Исследуем полученный ответ и дадим ему геометрическую интерпретацию:

1. Пусть

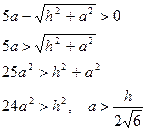
В этом случае прямые MN и CL пересекаются в первом квадранте (координата 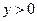) и окружность касается лучей СВ и СК (т.е. она вписана в угол ВСК).

2. Если вторая координата точки О отрицательна, то окружность касается луча СК и дополнения к лучу СВ (т.е. она вписана в угол, смежный углу ВСК).

3. Равенство означает, что MN параллельна биссектрисе CL.

Таким образом, мы, имея один подход к решению задачи, смогли охватить сразу три разных случая, и дали их интерпретацию.

Замечание 1:

Как мог заметить читатель, для нас не являлось самоцелью полное решение полученной системы уравнений, мы вычислили только те значения (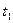 и R), которые нам нужны для решения задачи.

Замечание 2:

При решении задачи координатным способом очень важно анализировать полученное решение и давать ему интерпретацию (т.е., например, выяснить, имеют ли полученные результаты геометрический смысл: вдруг появилась отрицательная площадь или косинус угла имеет значение больше единицы; исследовать, как изменение тех или иных параметров влияет на расположение рассматриваемых геометрических объектов, и т.п.).

3.5. На плоскости даны две точки F₁ и F₂. Найдите геометрическое место точек М, таких, что сумма расстояний от точки M до точек F₁ и F₂ равно постоянному числу 2a.

Решение: Введем на плоскости систему координат так, чтобы точки имели координаты (-c,0) и (c,0). Пусть точка M имеет координаты (x,y). Расстояния от M до F₁ и F₂

выразятся так: 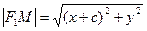и 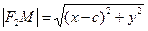. Сложим два этих корня и приравняем эту сумму к 2a:

.

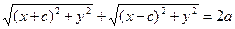Возведем обе части уравнения в квадрат, приведем подобные, сократим уравнение на 2, перенесем выражение, содержащее знак корня в правую часть, а a² – в левую часть и еще раз возведем левую и правую части полученного уравнения в квадрат. Получим:

.

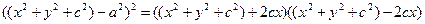Раскроем скобки, упростим выражение и приведем подобные. В результате получим:

.

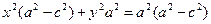Обозначим 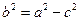и разделим в последнем равенстве левую и правую часть на 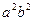. Получим уравнение: 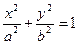. Фигура, задаваемая этим уравнением, называется эллипсом. Само же уравнение называют каноническим уравнением эллипса. Точки F₁ и F₂ называют фокусами эллипса, отрезки a и b (a>b) – полуосями эллипса.

Задание для самостоятельного решени я

Необходимо решить предложенные ниже задачи, оформить их решения отдельно от заданий по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.

М.10.11.1. Докажите, что прямая, проходящая через точку М₁(х₁; у₁) и М₂(х₂; у₂) может быть задана уравнением .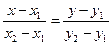

Указание: в уравнениях (2.3) §2 выразите параметр t и приравняйте правые части.

М.10.11.2. Векторы 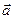и 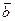образуют угол, докажите, что вектор 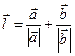лежит на биссектрисе этого угла.

М.10.11.3. Даны координаты вершин треугольника: А(0; 1), В(1; 0), С(6; -3), найдите параметрические уравнения биссектрисы угла .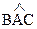

Указание: используйте результаты задач М.10.8.1 и М.10.8.3.

М.10.11.4. В условиях задачи 3.1.2 из §3 проверьте, могут ли векторы 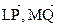и 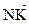служить сторонами треугольника.

М.10.11.5. АВСD – ромб со стороной 2 см и углом при вершине А в 60°. Введите систему координат, поместив ее начало в т. А, направив ось ОХ по прямой АВ, а ось OY – перпендикулярно к АВ, в ту сторону, с которой лежит сам ромб. Найдите координаты всех вершин ромба и точки пересечения его диагоналей.

М.10.11.6. Точки А(7; -1) и С(3; 0) – противоположные вершины прямоугольника АВСD. Найдите координаты двух других вершин, если стороны прямоугольника параллельны координатным осям.

М.10.11.7. Окружности радиусов r и R касаются внешним образом, прямая а – их общая касательная. Найдите радиус окружности, которая касается двух данных и прямой а.

М.10.11.8. Докажите, что площадь параллелограмма, координаты всех вершин которого – целые числа, целое число.

М.10.11.9. Решите систему

Указание: рассмотрите векторы с координатами (х; 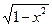) и (у; 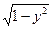), тогда левые части уравнений системы есть координаты суммы двух этих векторов. Рассмотрите длины трех этих векторов и убедитесь (докажите), что два первых – равны.

М.10.11.10. Докажите, что все точки параболы 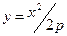обладают следующим свойством: расстояние от любой точки M параболы до точки F(0,p) равно расстоянию от точки M до прямой .

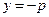(Точку F называют фокусом параболы, а прямую 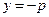- директрисой.)

М.10.11.11. Сколько точек с целочисленными координатами лежит внутри треугольника АВС если вершины имеют координаты: А(1,-1), В(3,-8), С(11,6).

[1] Повторите материал из главы IX, X и §3 главы XI из учебника геометрии 7-9, авторов Л.С. Атанасяна и др.

[2] Обращаем внимание читателей, что с термином “решетка” в математике связано несколько разных понятий.