 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Связь между непрерывностью и дифференцируемостью
|
|
Лекция 7.
Задачи, приводящие к понятию производной.
Производная, её механический, экономический и геометрический смысл.Правила дифференцирования.
Цель: Четкое представление понятия производной, её механического, экономического, геометрического смысла. Умение составить уравнение касательной к кривой. Понимание правил дифференцирования.
Задача: Овладение техникой дифференцирования.
7.1. Задачи, приводящие к понятию производной. Производная, её механический, экономический и геометрический смысл.
7.2. Связь между непрерывностью и дифференцируемостью.
7.3. Правила дифференцирования. Таблица производных.
Задачи, приводящие к понятию производной.
Определение производной.
Задача 1. Скорость прямолинейного неравномерного движения.
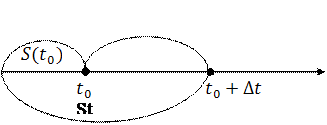 Пусть точка движется прямолинейно, неравномерно и известен закон движения S=S(t). Требуется найти мгновенную скорость точки.
Пусть точка движется прямолинейно, неравномерно и известен закон движения S=S(t). Требуется найти мгновенную скорость точки.
Очевидно, к моменту времени t 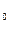 пройден путь S(t
пройден путь S(t 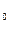 ). К моменту времени t= t
). К моменту времени t= t 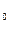 +
+ 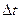 пройден путь S(t)=S(t
пройден путь S(t)=S(t 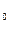 +
+ 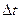 ). за промежуток времени
). за промежуток времени 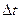 пройден путь
пройден путь 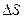 =S(t)-S(t
=S(t)-S(t 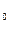 ) или
) или 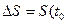 +
+ 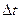 )- S(t
)- S(t 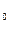 ). Средняя скорость в течение промежутка времени
). Средняя скорость в течение промежутка времени 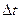 Vср=
Vср= 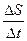 .
.
При малых значениях 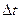 можно принять V(
можно принять V(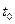 )
) 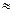 Vср.
Vср.
Мгновенная скорость: V(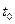 )=
)= 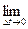 Vср=
Vср= 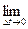
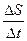 (7.1)
(7.1)
Задача 2. О производительности труда.
Пусть функция u(t) определяет количество произведенной продукции за время t. Найдем производительность труда в момент времени t 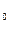 . За период времени t – t
. За период времени t – t 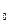 = Δt произведено продукции Δu = u(t
= Δt произведено продукции Δu = u(t 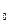 + Δt) – u(t
+ Δt) – u(t 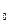 ).
).
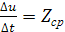 - средняя производительность труда в промежутке времени [t
- средняя производительность труда в промежутке времени [t 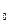 , t]. При малых Δt Z(t
, t]. При малых Δt Z(t 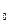 )
) 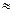 Zср=
Zср= 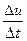 .
.
 Z(t
Z(t 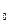 )=
)= 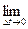
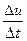 (7.2)
(7.2)
Задача 3. Линейная плотность стержня при неравномерном распределении массы.
p(x 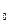 )=
)= 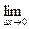 pср =
pср = 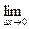
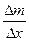 (7.3)
(7.3)
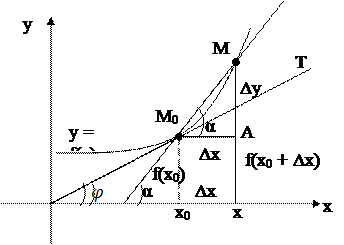
Задача 4. О касательной к кривой. 
Пусть точка М 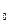 (х
(х 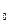 у
у 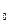 ) принадлежит кривой у=f(x). М(х,у)-произвольная точка на кривой. Пусть Δх → 0. Тогда х → х
) принадлежит кривой у=f(x). М(х,у)-произвольная точка на кривой. Пусть Δх → 0. Тогда х → х 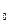 и точка М по кривой приближается к точке М
и точка М по кривой приближается к точке М 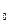 .Секущая М
.Секущая М 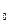 М поворачивается вокруг точки М
М поворачивается вокруг точки М 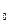 , стремясь занять положение касательной М
, стремясь занять положение касательной М 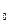 Т.
Т.
В этом случае α→ φ, tg 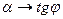
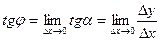
Kkac= 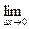
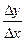 (7.4)
(7.4)
 Рассматривая четыре различные по смысловому содержанию задачи, обнаруживаем, что они совершенно одинаковы по математической структуре: находим
Рассматривая четыре различные по смысловому содержанию задачи, обнаруживаем, что они совершенно одинаковы по математической структуре: находим
1. Значение некоторой величины в начальный момент(или в начальной точке);
2. Приращение этой величины в зависимости от приращения аргумента(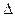 S,
S, 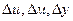 );
);
3. Среднюю скорость изменения этой величины (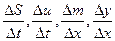 );
);
4. Переходим к пределу.
Эти пределы играют чрезвычайно важную роль в математическом анализе и вообще в математике, являясь основным понятием теории дифференциального исчисления.
Замечание. Любое изменение одной величии относительно другой можно понимать как движение (прогресс).
Под скоростью движения понимается изменение одной величины, отнесенное к единице другой величины.
Рассмотрим произвольную функцию y=f(x).
Пусть y=f(x) непрерывна в точке х и некоторой её окрестности. Если аргумент х получил приращение 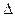 х, то функция получила приращение
х, то функция получила приращение 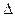 у.
у.
Согласно схеме (1)-(4)можно составить отношение 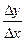 .
.
 Определение. Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю(если этот предел существует) называется производной функции f(x).
Определение. Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю(если этот предел существует) называется производной функции f(x).
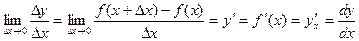 (7.5)
(7.5)
Операция отыскания производной называется дифференцированием функции. Функция, имеющая в точке х производную, называется дифференцируемой в этой точке. Раздел математики, занимающийся теорией производных, называется дифференциальным исчислением.
В соответствии с определением производной и пределами (1)-(4) следует:
V(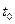 )= )= 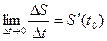 ; ; 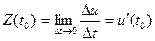 ρ
ρ 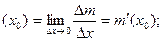 k= k= 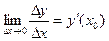
|
(7.6)
Из (7.6) следует:
· С механической точки зрения: 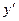 -мгновенная скорость движения в момент времени
-мгновенная скорость движения в момент времени 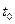 ;
;
· Экономический смысл производной: 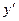 -мгновенная производительность труда
-мгновенная производительность труда 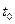 ;
;
· Геометрический смысл производной: 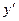 - угловой коэффициент касательной к кривой в точке М
- угловой коэффициент касательной к кривой в точке М 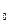 .
.
Уравнение касательной к кривой в точке М 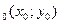 имеет вид:
имеет вид:
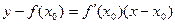 . (7.7)
. (7.7)
Связь между непрерывностью и дифференцируемостью.

 Теорема. Если функция у=f(x) дифференцируема в точке
Теорема. Если функция у=f(x) дифференцируема в точке 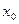 , то она в ней непрерывна.
, то она в ней непрерывна.
Доказательство. Функция у=f(x) дифференцируема в точке 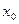 ,следовательно существует:
,следовательно существует:
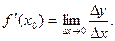
В этом случае 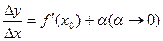 ,откуда получаем
,откуда получаем
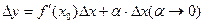 ,
,
Следовательно 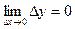 ,
,
Т.е у=f(x) непрерывна в точке 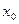 .
.
Таким образом, дифференцируемость функции есть достаточное условие непрерывности функции (из дифференцируемости функции следует её непрерывность).
Обратное утверждение неверно, то есть из непрерывности не вытекает дифференцируемость функции.
Например, у=|х|. (Рис.7.2.3)
Рис.7.2.3
Найдем 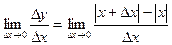 .
.
Если 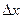 >0, то
>0, то 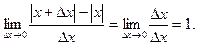
Если 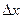 <0,то
<0,то 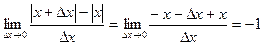 .
.
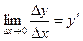 не существует.
не существует.
Функция у= 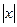 в точке х=0 непрерывна, но не дифференцируема (нет единственной касательной). Непрерывность- необходимое, но не достаточное условие дифференцируемости.
в точке х=0 непрерывна, но не дифференцируема (нет единственной касательной). Непрерывность- необходимое, но не достаточное условие дифференцируемости.
Рис 7.1.4
Функции, представленные на рис 7.1.4 не дифференцируемы, в точках 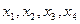 хотя и непрерывны.
хотя и непрерывны.
Условие дифференцируемости соответствует условию гладкости кривой.
Дата публикования: 2015-11-01; Прочитано: 934 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
