 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Постановка задачи. Если , и непрерывны в окрестности корня, эту дополнительную информацию о свойствах функции
|
|
Если 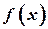 ,
, 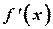 и
и 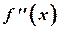 непрерывны в окрестности корня, эту дополнительную информацию о свойствах функции
непрерывны в окрестности корня, эту дополнительную информацию о свойствах функции 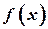 можно использовать для построения алгоритмов, которые порождают последовательности, которые сходятся к корню быстрее, чем при методе деления пополам. Метод Ньютона-Рафсона (или просто Ньютона, также имеет название метод касательных и метод линеаризации) является одним из наиболее полезных и известных алгоритмов, в котором используется непрерывность первой и второй производной. Он быстро сходится и допускает различные модификации, применяемые для решения отдельных задач. Однако этот метод является эффективным при достаточно жестких ограничениях на характер функции
можно использовать для построения алгоритмов, которые порождают последовательности, которые сходятся к корню быстрее, чем при методе деления пополам. Метод Ньютона-Рафсона (или просто Ньютона, также имеет название метод касательных и метод линеаризации) является одним из наиболее полезных и известных алгоритмов, в котором используется непрерывность первой и второй производной. Он быстро сходится и допускает различные модификации, применяемые для решения отдельных задач. Однако этот метод является эффективным при достаточно жестких ограничениях на характер функции 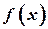 :
:
1. существование второй производной функции 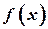 на множестве
на множестве 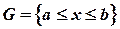 ;
;
2. выполнение первого условия 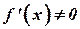 для всех
для всех 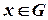 ;
;
3. знакопостоянство 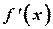 ,
, 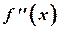 для всех
для всех 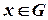 .
.
Геометрическая интерпретация метода Ньютона состоит в следующем. Задается начальное приближение 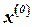 . Далее проводится касательная к кривой
. Далее проводится касательная к кривой 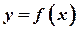 в точке
в точке 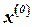 (рис. 5.1), то есть кривая заменяется прямой линией. В качестве следующего приближения выбирается точка пересечения этой касательной с осью абсцисс. Процесс построения касательных и нахождение точек пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше заданной величины
(рис. 5.1), то есть кривая заменяется прямой линией. В качестве следующего приближения выбирается точка пересечения этой касательной с осью абсцисс. Процесс построения касательных и нахождение точек пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше заданной величины 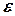 .
.
Получаем расчетную формулу метода Ньютона. Вместо участка кривой ВС (точка С соответствует 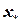 ) возьмем участок АВ – касательную, проведенную в точке с координатами
) возьмем участок АВ – касательную, проведенную в точке с координатами 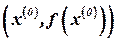 . Для этого отрезка справедливо конечное соотношение:
. Для этого отрезка справедливо конечное соотношение:
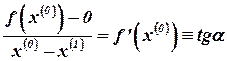 (4.7)
(4.7)
где 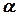 - угол наклона касательной в точке
- угол наклона касательной в точке 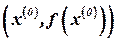 к оси абсцисс.
к оси абсцисс.
Решая (4.7) относительно 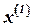 , получаем:
, получаем:

Рис. 4.7 Геометрические построения для метода Ньютона
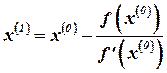 (4.8)
(4.8)
Повторяя процесс, находим общую формулу:
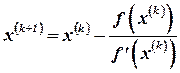
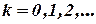 (4.9)
(4.9)
Отметим, что если убрать итерационный индекс, то (4.9) перепишется в виде нелинейного уравнения:
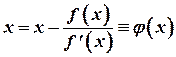 (4.10)
(4.10)
которое, однако, на 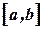 не будет эквивалентным исходному, а является таким только в одной точке при
не будет эквивалентным исходному, а является таким только в одной точке при 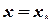 .
.
Применим теперь для получения формулы (4.9) метод линеаризации. Предположим, что процесс итераций имеет вид:
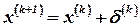 , где
, где 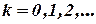 (4.11)
(4.11)
где 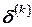 - поправка для
- поправка для 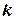 - го приближения, которое нужно найти. Предполагая, что
- го приближения, которое нужно найти. Предполагая, что 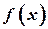 имеет непрерывную вторую производную, разложим
имеет непрерывную вторую производную, разложим 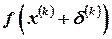 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 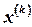 :
:
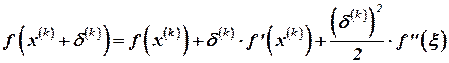 (4.12)
(4.12)
где 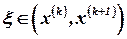 . Учитывая то, что
. Учитывая то, что 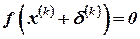 (что соответствует нахождению точки пересечения с осью абсцисс), и, оставляя только линейную (относительно
(что соответствует нахождению точки пересечения с осью абсцисс), и, оставляя только линейную (относительно 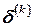 ) часть разложения (отсюда и название – метод линеаризации), запишем линейное уравнение относительно
) часть разложения (отсюда и название – метод линеаризации), запишем линейное уравнение относительно 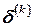 :
:
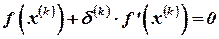 (4.13)
(4.13)
Отсюда можно найти поправку 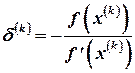 . Подставляя
. Подставляя 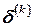 в (4.11), получим (4.9).
в (4.11), получим (4.9).
Замечание:
1) Из рис. 4.7 можно заметить, что если начать строить касательные из точки а, то найдется 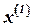 не принадлежащая интервал
не принадлежащая интервал 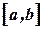 , где функция может быть даже не определенной. Таким образом, можно сформулировать правило выбора начальной точки
, где функция может быть даже не определенной. Таким образом, можно сформулировать правило выбора начальной точки 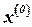 : в качестве начальной точки
: в качестве начальной точки 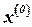 берем тот конец интервала
берем тот конец интервала 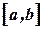 , которому соответствует ордината с тем же знаком, что и знак
, которому соответствует ордината с тем же знаком, что и знак 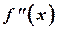 .
.
Это правило можно записать в виде формулы:
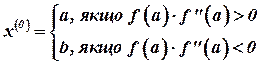 (4.14)
(4.14)
2) Из графической аналогии метода очевидным является требование сохранения знаков 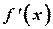 и
и 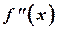 : функция на отрезке
: функция на отрезке 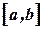 не должна иметь перегибов и изменение монотонности.
не должна иметь перегибов и изменение монотонности.
Теорема (о достаточных условиях сходимости метода Ньютона):
Пусть выполняются условия:
1. Функция 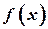 определена и дважды непрерывно дифференцируемая на отрезке
определена и дважды непрерывно дифференцируемая на отрезке 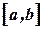 .
.
2. Отрезку 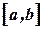 принадлежит только один простой корень
принадлежит только один простой корень 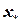 , такой что
, такой что 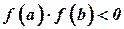 .
.
3. Производные 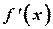 ,
, 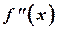 на
на 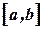 сохраняют знак, и
сохраняют знак, и 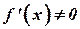 .
.
4. Начальное приближение 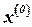 удовлетворяет неравенству
удовлетворяет неравенству 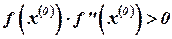 (знаки функций
(знаки функций 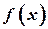 и
и 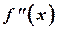 в точке
в точке 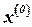 сходятся).
сходятся).
Тогда при помощи метода Ньютона (9) можно вычислить корень уравнения 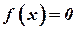 с произвольной точностью
с произвольной точностью 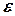 .
.
Дата публикования: 2015-11-01; Прочитано: 175 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
