Критерии согласия

Рассмотри один из вопросов, связанных с проверкой правдоподобия гипотез, а именно – вопрос о согласовании теоретического и статистического распределения. Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (например 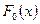), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону 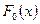. Более того, пусть данное статистическое распределение выровнено с помощью некоторой теоретической кривой 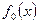. Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Возникает вопрос: объясняются ли расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связанны с тем что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос служат т.н. «критерии согласия».

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Идея применения критериев согласия заключается в следующем. На основании данного статистического материала нам предстоит проверить гипотезу 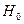, состоящую в том, что случайная величина Х подчиняется некоторому определенному закону распределения. Этот закон может быть задан в той или иной форме: например, в виде функции распределения 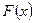или в виде совокупностей вероятностей 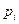, где 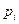- вероятность того, что величина Х попадает в пределы i – го разряда (интервала). Функция распределения 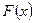является наиболее общей формой закона распределения. Поэтому будем формулировать гипотезу 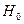, как состоящую в том, что случайная величина Х имеет известную функцию распределения 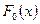. Т. Е. относительно теоретической функции распределения (функция распределения генеральной совокупности) 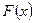выдвигается две непараметрические (см. параграф 11.1) гипотезы: простая нулевая 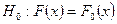и сложная конкурирующая .

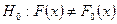На практике применяют критерии согласия 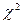(«хи-квадрат») Пирсона, Колмогорова, Смирнова (Николай Васильевич Смирнов (1900-1966)-советский математик [18, с. 455]), 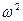(«омега-квадрат») и др.

Наиболее часто употребим критерий Пирсона. Опишем, как он применяет к проверке гипотезы о нормальном распределении генеральной совокупности. Заметим, что этот критерий аналогично применяется и для других распределений, и этот факт – несомненное преимущество.

Итак, пусть проведена серия опытов, в результате которой получена выборка объема 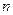. По выборке составлено статистическое распределение:

Табл. 1 Статистическое распределение

Варианты			…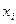
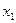
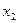
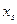
Эмпирические частоты			…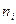

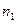
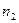
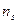
Естественно, что 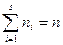. Кроме того, в предположении нормального распределения мы вычислили (точнее, ценили) частоты 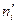теоретического распределения. При уровне значимости 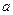требуется проверить нулевую гипотезу 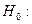генеральная совокупность распределена нормально.

Будет ли случайным расхождение частот? Может быть, что расхождение случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо иными причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности. Критерий Пирсона отвечает на поставленный вопрос. Однако, как и любой критерий, он не доказывает справедливости гипотезы, 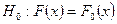лишь устанавливает на допустимом уровне значимости 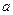ее согласие или несогласие с данными наблюдений.

Как и ранее для того что принять или опровергнуть гипотезу 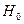, нам следует ввести некоторою случайную величину 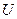, характеризующую степень расхождения теоретического и статистического распределений. Величина 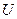может быть выбрана различными способами. Например, в качестве 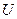можно взять сумму квадратов отклонений теоретических частот 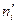от соответствующих наблюдаемых частот 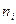. Или же сумму тех же квадратов отклонений с некоторыми коэффициентами («весами»). Или же максимальное отклонение статистической функции распределения 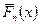от теоретической 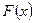и т. д.

При использовании критерия Пирсона для проверки нулевой гипотезы рассматривают случайную величину

.

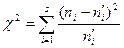Эта величина, действительно, является случайной, т.к. в различных опытах она принимает различные, заранее неизвестные значения. Понятно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия 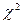. Следовательно, он в определенном смысле характеризует близость эмпирического и теоретического распределений.

Обсудим сам вид критерия. Итак, возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей. Делением на 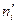достигают уменьшения каждого из слагаемых. В противном случае сумма была бы велика и это приводило бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива. Доказано, что при 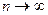закон распределения введенной случайной величины независимо от того, какому закону подчинена генеральная совокупность, стремится к закону распределения 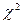с k степенями свободы. Число степеней свободы равно

,

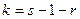Где s – число групп (частичных интервалов) выборки, r – число параметров предполагаемого распределения. Параметры оцениваются по данным выборки. Например, если предполагаемое распределение – нормально, то оценивают два параметра – математического ожидание и среднее квадратическое отклонение. Следовательно, r = 2, поэтому число степеней свободы .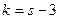

В силу того, что односторонний критерий более категорично отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область. При этом будем требовать, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости :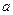

.

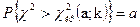Обозначим наблюдаемое значения критерия 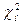и сформулируем правило проверки нулевой гипотезы.

Рассмотрим задачу проверки гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

Правило. Для того чтобы при заданном уровне значимости 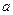проверить нулевую гипотезу 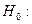генеральная совокупность распределена нормально, надо вычислить теоретические частоты 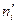, а затем наблюдаемое значение критерия

.

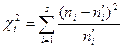Затем по таблице критических точек распределения 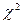(приложение 5) при заданном уровне значимости 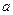и числе степеней свободы 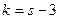находят критическую точку 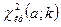. Если окажется, что 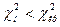, то нет оснований отвергать нулевую гипотезу. В противном случае ее отвергают.

В учебнике [8, гл. 19, § 23] приведены замечания, освещающие особенности применения критерия Пирсона. Приведем их.

Замечание 1. Объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа должна содержать не менее 5-8 вариант. Малочисленные группы следует объединить в одну, суммируя частоты.

Замечание 2. Поскольку возможны ошибки первого и второго рода, и особенности, если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями, построить график распределения, вычислить асимметрию и эксцесс.

Замечание 3. Для контроля вычислений формулу, по которой вычисляют наблюдаемое значение критерии я, преобразуют виду

.

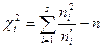учитывая, что 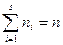и .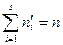

Пример 1. Автомойка каждые три часа фиксирует количество обслуженных грузовых машин. Данные собираются в течение суток. При уровне значимости 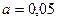проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические 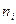и теоретические 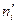частоты:

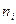
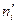
Решение. Вычисления необходимые для определения наблюдаемого значения критерия приведем в табл. 2.

Табл. 2. Расчет наблюдаемого значения критерия Пирсона

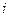
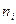
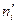
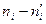
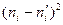
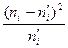
			-2 -4 -10		0,25 0,266667 0,4 0,202532 0,164948 0,333333 0,121212

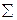
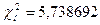
Число степеней свободы, учитывая, что число групп выборки (число различных вариантов) s = 8, равно k = 8 - 3 = 5. По таблице приложения 5 находим 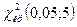= 11,07048.

Т.к. 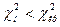, то нет оснований отвергать нулевую гипотезу. Иными словами, расхождение эмпирических и теоретических частот незначимое. Т.о., данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

Этот пример легко выполняется с помощью Microsoft Excel. Наблюдаемое значение критерия:

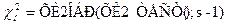
Критическая же точка находится как

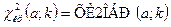
Сущность критерия согласия Пирсона состоит в сравнении эмпирических и теоретических частот. Понятно, что эмпирические частоты находят из опыта. Как найти теоретические частоты, если предполагается, что генеральная совокупность распределена нормально? Ниже приведен один из способов решения этой задачи.

1) Весь интервал наблюдаемы значений Х (выборки объема n) делят на s частичных интервалов одинаковой длины. Находят середины частичных интервалов 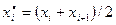. В качестве частоты 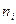варианты 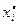принимают число вариант, которые попали в i -й интервал. В итоге имею последовательность равностоящих вариант и соответствующих им частот:

Варианты			…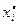
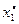
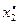
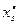
Эмпирические частоты			…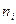

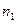
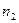
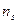
Естественно, что .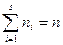

2) Вычисляют выборочную среднюю 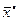и выборочное среднее квадратическое отклонение .

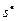3) Центрируют и нормируют случайную величину Х, т.е. переходят к величине 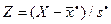и вычисляют концы интервалов :

, ,

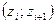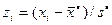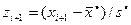причем наименьшее значение Z, т.е. 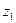, полагают равным - 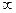, а наибольшее, т.е. 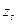, полагают равным .

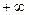4) Вычисляют теоретические вероятности 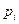попадания случайной величины Х в интервалы 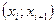по формуле

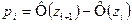
где 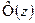- интегральная функция Лапласа (см. приложение 2)

5) Находят искомые теоретические частоты

.

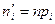После применения описанного способа нахождения теоретических частот, естественно, можно использовать то же правило проверки нулевой гипотезы.

Пример 2. ОТК проверил время обработки (в минутах) 100 деталей. В итоге, получена выборка объема 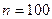, заданная интервальным распределением:

Интервал	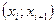(0;10)	(10;20)	(20;30)	(30;40)	(40;50)
Частота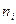

При уровне значимости 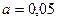проверить гипотезу о нормальном распределении генеральной совокупности.

Решение. Эмпирические частоты попадания в интервалы заданы. Определим теоретические частоты, предполагая, что генеральная совокупность распределена нормально.

1) Весь интервал наблюдаемых значений Х (выборки объема 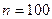) уже разделена на 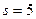частичных интервалов одинаковой длины. Найдем середины частичных интервалов 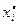. В качестве частоты 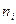варианты 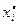примем число вариант, которые попали в i –й интервал. В итоге получаем статистическое распределение равноотстоящих вариант и соответствующих их частот:

Вариант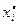
Частота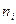

2) Выборочная средняя равна 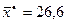. Выборочное среднее квадратическое отклонение равно .

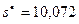3) Вычисляем концы интервалов 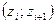(см. табл. 3)

Табл. 3. Нахождение концов интервалов

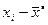
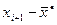
i	Границы интервала			Границы интервала
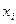
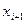
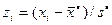
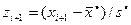
			-16,6 -6,6 3,4 13,4	-16,6 -6,6 3,4 13,4	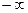-1,64813 -0,65528 0,337569 1,330421	-1,64813 -0,65528 0,337569 1,330421

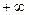
4) Вычисляем теоретические вероятности 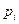(см. табл. 4).

5) Находим искомые теоретические частоты 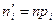(см. табл. 4).

Табл.4 Нахождение теоретических вероятностей и частот

i	Границы интервала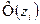
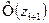
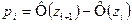
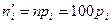
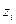
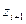
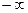	-1,64813 -0,65528 0,337569 1,330421	-1,64813 -0,65528 0,337569 1,330421	-0,5 0,45034 -0,24386 0,132156 0,40831	-0,45034 -0,24386 0,132156 0,40831 0,5	0,049663 0,20648 0,376013 0,276154 0,09169	4,966263 20,64804 37,60131 27,6154 9,168987

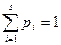
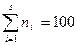
Вычисления необходимые для определения наблюдаемого значения критерия приведем в табл. 5.

Табл. 5. Расчет наблюдаемого значения критерия Пирсона

i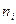
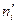
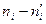
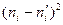
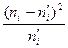
		4,966263 20,64804 37,60131 27,6154 9,168987	1,033737 -4,64804 6,398692 -3,6154 0,831013	1,068612 21,60429 40,94326 13,07113 0,690583	0,215174 1,046312 1,088879 0,473327 0,075317

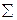
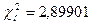
Число степеней свободы, учитывая, что число групп выборки, равно 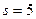, равно 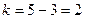. По таблице приложения 5 находим .

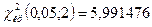Т.к. 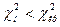, то нет оснований отвергать нулевую гипотезу. Иными словами, расхождение эмпирических и теоретических частот незначимое. Т.о., данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

Замечание 4. Описанная процедура нахождения теоретических частот подходит и при гипотезе о других видах распределений. Естественно, вероятности 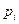будут вычисляться по-другому. Например, если выдвигается гипотеза о показательном распределении, то

,

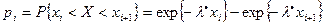где 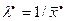. В [7, гл. 13] рассматриваются гипотезы об основных известных распределениях.

Кроме критерия 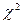, для оценки степени согласованности теоретического и статистического распределений на практике чаще всего применяются критерий Колмогорова.

В качестве меры расхождения между теоретическим и статистическим распределениями рассматривается максимальное значение модуля разности между статистической функцией распределения 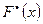и соответсвующей теоретической функцией распределения :

.

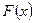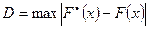Аргументы в пользу этого критерия – простота вычисления величины 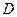и то, что ее распределение также имеет достаточно простой вид.

А. Н. Колмогоров доказал, что какова бы ни была функция распределения 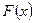непрерывной случайной величины Х, при ограничении возрастания числа независимых наблюдений n вероятность неравенства

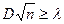
стремится к пределу

.

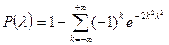Значения вероятности 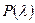приведены в табл. 6.

Табл. 6. Предельные вероятности критерия Колмогорова

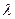
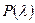
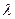
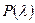
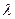
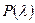
0,0 0,1 0,2 0,3 0,4 0,5 0,6	1,000 1,000 1,000 1,000 0,997 0,964 0,864	0,7 0,8 0,9 1,0 1,1 1,2 1,3	0,711 0,544 0,393 0,270 0,178 0,112 1,068	1,4 1,5 1,6 1,7 1,8 1,9 2,0	0,040 0,022 0,012 0,006 0,003 0,002 0,001

Изложим схему применения критерия Колмогорова. Итак, на одном график строятся статистическая функция распределения 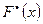и предполагаемая теоретическая функция распределения 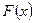. Затем, определяется максимум 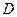модуля разности между нами (рис. 1).

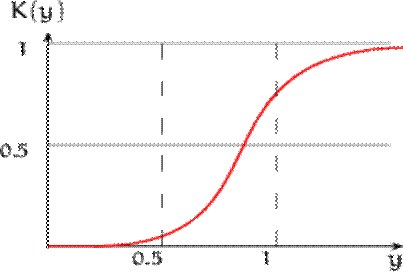
Рис. 1. Графическая иллюстрация к критерию согласия Колмогорова

После этого требуется определить величину

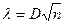
и по табл. 6 найти вероятность 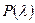. Это будет вероятность того, что (если случайная величина Х действительно распределена по закону 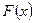) за счет чисто случайных причин максимальное расхождение между 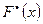и 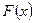будет не меньше, чем фактически наблюдаемое. При сравнительно больших 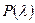нет оснований отвергать нулевую гипотезу.

Замечание 5. Критерий Колмогорова проще критерия 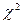Пирсона, поэтому его весьма охотно применяют на практике. Следует, однако, сказать, что этот критерий можно применять только в случае, когда гипотетическое распределение 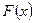полностью известно заранее из каких-либо теоретических соображений, т.е. когда известен не только вид функций распределения 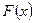, но и все входящие в нее параметры. Такой случай сравнительно редко встречается на практике. Обычно из теоретических соображений известен только общий вид функций 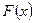, а входящие в нее числовые параметры определяются по данному статистическому материалу. При применении критерия 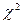Пирсона это обстоятельство учитывается соответствующим уменьшением числа степеней свободы распределения 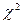. Критерий Колмогорова такого согласования не предусматривает. Если все же применять этот критерий в тех случаях, когда параметры теоретического распределения выбираются по статистическим данным, критерий дает заведомо завышенные значения вероятности 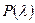. Поэтому в ряде случаев есть риск принять как правдоподобную гипотезу, которая в действительности плохо согласуется с опытными данными.