Сравнение двух дисперсий нормальных генеральных совокупностей

Тема: Критерий Фишера о равенстве (неравенстве) двух дисперсий.

Часто на практике возникает задача сравнения дисперсий. Это связано с потребностью сопоставлять точность приборов, инструментов, самих методов измерений и т. д. Естественно, предпочтительнее тот инструмент, который обеспечивает наименьшее рассеивание результатов измерений, т.е. наименьшую дисперсию.

Сравнение двух дисперсий нормальных генеральных совокупностей.

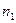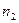Пусть генеральные совокупности X и Y распределены нормально. Из совокупностей извлечены выборки объема и , соответственно. По ним найдены исправленные выборочные дисперсии и 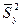. Требуется по исправленным дисперсиям при заданном уровне значимости 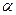проверить нулевую гипотезу. Она состоит в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

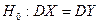В силу того, что исправленные дисперсии являются несмещенными оценками генеральных дисперсий, т.е.

,

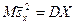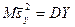
нулевую гипотезу можно записать следующим образом:

.

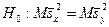Т.о. требуется проверить, что математические ожидания исправленных выборочных дисперсий равны между собой. Обычно исправленные дисперсии оказываются различными. Значимо (существенно) или незначимо различаются исправленные дисперсии?

Если окажется, что нулевая гипотеза справедлива, т. е. генеральные дисперсии одинаковы, то различие исправленных дисперсий незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки. Например, если различие исправленных выборочных дисперсий результатов измерений, выполненных двумя приборами, оказалось незначимым, то приборы имеют одинаковую точность. Если же нулевая гипотеза отвергнута, т.е. генеральные дисперсии неодинаковы, то различие исправленных дисперсий значимо и не может быть объяснено случайными причинами.

В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий принимают отношение большей исправительной дисперсии к меньшей, т.е. случайную величину

.

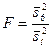Величина F при условии справедливости нулевой гипотезы имеет распределение Фишера-Снедекора со степенями свободы 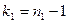и , где 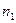– объем выборки, по которой вычислена большая исправленная дисперсия, 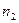– объем выборки, по которой найдена меньшая дисперсия. Распределение Фишера-Снедекора зависит только от чисел степеней свободы и не зависит от других параметров. Этот критерий называют критерием Фишера-Снедекора. Для него имеются специальные таблицы (см. приложение 7).Критическая область строится в зависимости от вида конкурирующей гипотезы.

В качестве первого случая рассмотрим нулевую гипотезу 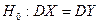и конкурирующую гипотезу 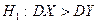. Построим правостороннюю критическую область. Потребуем, чтобы вероятность попадания критерия 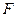в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 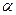, т.е.

.

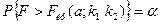Критическая точка находится по таблице критических точек распределения Фишера-Снедекора. Обозначим отношение большей из наблюдаемых исправленных дисперсий к меньшей, как 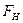. Сформулируем правило проверки нулевой гипотезы.

Для того чтобы при заданном уровне значимости проверить нулевую гипотезу 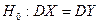о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе 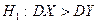, надо вычислить отношение большой исправленной дисперсии к меньшей, т.е.

.

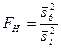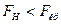По таблице критических точек распределения Фишера-Снедекора находят . Если , то нет оснований отвергать нулевую гипотезу. В противном же случае ее отвергают. Если использовать статистические функции из Microsoft Excel, то для нахождения надо вычислять FРАСПОБР .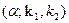

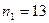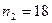Пример1. По двум независимым выборкам с объемами и , которые извлечены из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперси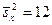и и 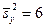. При уровне значимости 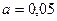проверить нулевую гипотезу 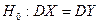о равенстве генеральных дисперсий при конкурирующей гипотезе .

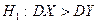Решение. Найдем отношение большей исправленной дисперсии к меньшей:

.

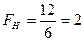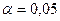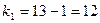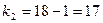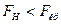Далее используем таблицу критических точек распределения F Фишера-Снедекора. По заданному уровню значимости и числам степеней свободы и находим критическую точку . Т.к. , то нет оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. Использование Microsoft Excel приводит к аналогичным результатам:

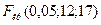=FPАСПОБР ;

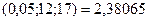В качестве второго случая рассмотрим нулевую гипотезу 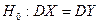и конкурирующую гипотезу 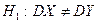. В этом случае надо строить двустороннюю критическую область. Можно доказать, что наибольшая мощность (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда вероятность попадания критерия в каждый из двух интервалов критической области равна . 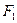Обозначим через левую границу критической области и через F ₂ – правую. Тогда должны выполняться соотношения

, .

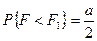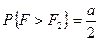Правую критическую точку 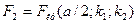находят по таблице критических точек распределения Фишера-Снедекора.

Оказывается, что левую критическую точку можно и не отыскивать. Достаточно найти правую критическую точку 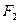при уровне значимости, вдвое меньше заданного. Тогда не только вероятность попадания критерия в «правую часть» критической области (т.е. правее 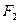) равна , но и вероятность попадания этого критерия в «левую часть» критической области (т.е. левее F ₁) также равна 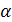/2. Т.к. эти события несовместны, то вероятность попадания рассматриваемого критерия во всю двустороннюю критическую область будет равна .

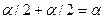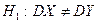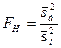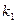Сформулируем правило проверки нулевой гипотезы о равенстве генеральных дисперсий нормально распределенных совокупностей при конкурирующей гипотеза . Для этого нужно вычислить отношение большой исправленной дисперсии к меньшей, т.е. . По таблице критических точек распределения Фишера-Снедекора по уровню значимости (вдвое меньшем заданного) и числам степеней свободы и 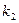( 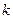– число степеней свободы большей дисперсии) найти критическую точку 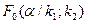. Если 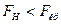, то нет оснований отвергать нулевую гипотезу. В противном же случае ее отвергают.

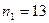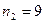Пример 2. По двум независимым выборкам с объемами и , которые извлечены из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперси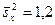и и 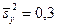. Требуется при уровне значимости проверить нулевую гипотезу 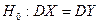о равенстве генеральных дисперсий при конкурирующей гипотезе .

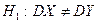Решение найдем отношением большей исправленной дисперсии к меньшей:

.

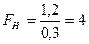Теперь используем таблиц критических точек распределения F Фишера-Снедекора. По заданному уровню значимости 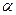/2=0,1/2=0,05 и числами степеней свободы 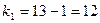и находим критическую точку 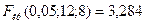. Использование Microsoft Excel приводит к аналогичным результатам:

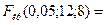FPАСПОБР .

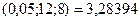Т.к. 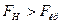, то нулевую гипотезу о равенстве генеральных дисперсий отвергаем. Другими словами, выборочные исправленные дисперсии различаются значимо. Например, если бы рассматриваемые дисперсии характеризовали точность двух методов измерений, то следует предпочесть тот метод, который имеет меньшую дисперсию (судя по нашему примеру 0,3).

Задача сравнения исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности.

Пусть генеральная совокупность распределена нормально, причем генеральная дисперсия хотя и неизвестна, но имеются основания предполагать, что она равна гипотетическому (предполагаемому) значению. На практике 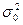устанавливается на основании предшествующего опыта или теоретически. Пусть из генеральной совокупности извлечена выборка объема п и по ней найдена исправленная выборочная дисперсия с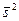 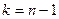степенями свободы. Требуется по исправленной дисперсии при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральная дисперсия рассматриваемой совокупности равна гипотетическому значению 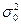. Т.к. 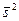является несмещенной оценкой генеральной дисперсии, имеем нулевую гипотезу

.

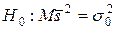Итак, требуется проверить, что математическое ожидание исправленной дисперсии равно гипотетическому значению генеральной дисперсии. Другими словами, надо установить, значимо или незначимо различаются исправленная выборочная и гипотетическая генеральная дисперсии.

На практике рассматриваемая гипотеза проверяется, если нужно проверить точность приборов, инструментов, станков, методов исследования и устойчивость технологических процессов. Например, известна допустимая характеристика рассеяния контролируемого размера деталей, изготавливаемых станков-автоматов, равная 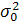. Если найденная по выборке характеристика окажется значимо больше 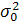, то станок нуждается в наладке.

Критерием проверки нулевой гипотезы является случайная величина

.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

Рассмотрим первый случай. Пусть нулевая гипотеза 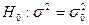. Конкурирующая гипотеза 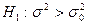. В этом случае строят правостороннюю критическую область и требуют, чтобы выполнялось соотношение

.

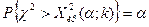Сформулируем правило проверки нулевой гипотезы. Надо вычислить наблюдаемое значение критерия 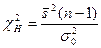. Затем по таблице критических точек распределения 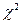(см. приложение 5), по заданному уровню значимости 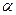и числу степеней свободы 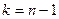, найти критическую точку 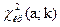. В Microsoft Excel критическая точка находится следующим образом 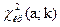=ХИ2ОБР.

Если 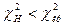, то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

Пример 3. Из нормальной генеральной совокупности извлечена выборка объема 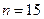и по ней найдена исправленная выборочная дисперсия 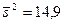. Требуется при уровне значимости 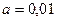проверить нулевую гипотезу 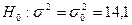, приняв в качестве конкурирующей гипотезы .

Решение. Найдем наблюдавшееся значение критерия:

.

Согласно конкурирующей гипотезе, критическая область является правосторонней. Из таблицы приложения 5 по уровню значимости 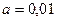и числу степеней свободы 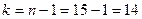находим критическую точку 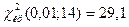. В Microsoft Excel получаем 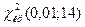=ХИ2ОБР(14;0,01)=29,141. Т.к. 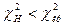, то нет оснований отвергать нулевую гипотезу. Другими словами, различие между исправленной дисперсией 14,9 и гипотетической генеральной дисперсией 14,1 – незначимое.

Рассмотрим теперь второй основной случай проверки гипотез. Нулевая гипотеза 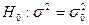. Конкурирующая гипотеза 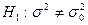. В этом случае строят двустороннюю критическую область. При этом исходят из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 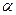. Критические точки – левую и правую границы критической области – находят, требуя, чтобы вероятность попадания критерия в каждый из двух интервалов критической области была равна 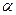/2:

, .

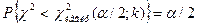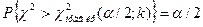В таблице критических точек распределения указаны лишь «правые» критические точки, поэтому возникает кажущееся затруднение в отыскании «левой» критической точки. Это затруднение легко преодолеть, если принять во внимание, что события 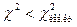и 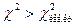противоположны и, следовательно,

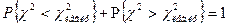
Отсюда

.

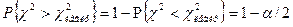Т.е. левую критическую точку можно искать как правую (и значит, ее можно найти по таблице, исходя из требования, чтобы вероятность попадания критерия в интервал, расположенный правее этой точки, была равна .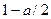

Сформулируем правило проверки нулевой гипотезы. Для того чтобы при заданном уровне значимости 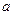проверить нулевую гипотезу о равенстве неизвестной генеральной дисперсии нормальной совокупности гипотетическому значению 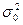при конкурирующей гипотезе 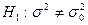, надо вычислить наблюдаемое значение критерия 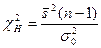и по таблице найти левую критическую точку и правую критическую точку 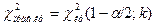. Если окажется, что

,

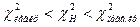то нет оснований отвергнуть нулевую гипотезу. Если же окажется, что 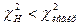или 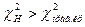, то нулевую гипотезу отвергают.

Пример 4. Из нормальной генеральной совокупности извлечена выборка объема п= 16 по ней найдена исправленная выборочная дисперсия 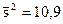. Требуется при уровне значимости 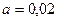проверить нулевую гипотезу , приняв в качестве конкурирующей .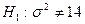

Решение. Найдем наблюдавшееся значение критерия:

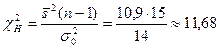
Судя по конкурирующей гипотезе, критическая область будет двусторонней. По таблицам приложения 5 находим критические точки:

;

= .

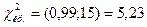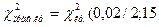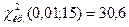Т.к. наблюдавшееся значение критерия принадлежит области принятия гипотез:

,

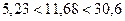то нет оснований ее отвергать. Другими словами, исправленная выборочная дисперсия 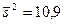незначимо отличается от гипотетической генеральной дисперсии .

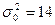В третьем случае конкурирующая гипотеза имеет вид

.

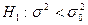При такой конкурирующей гипотезе находят критическую точку 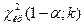. Если окажется, что

,

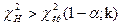то нет оснований отвергать нулевую гипотезу. В противоположном случае ее отвергают.

Замечание 1. Если число степеней свободны 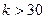, то критическую точку можно приближенно найти по равенству Уилсона-Гилферти

,

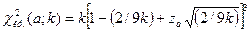где z_α определяют из равенства

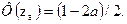
используя таблицы интегральной функции Лапласа (приложение 2).

3.Рассмотрим задачу сравнения нескольких (более двух) дисперсий нормальных генеральных совокупностей. Имеем l генеральных совокупностей X ₁, X ₂,…, X_l, которые распределены нормально. Из этих совокупностей извлечены независимые выборки, вообще говоря, различных объемов п ₁, п ₂,…, п_l. Случай выборок одинакового объема будет рассматриваться в данном параграфе несколько позднее. По выборкам найдены исправленные выборочные дисперсии .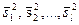

Требуется по исправленным выборочным дисперсиям при заданном уровне значимости 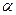проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

Иными словами, требуется установить, значимо или незначимо различаются исправленные выборочные дисперсии. Такую гипотезу принято называть гипотезой об однородности дисперсий.

Напомним, что числом степеней свободы дисперсии 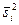называют число, на единицу меньше объема выборки, т.е. 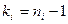. Введем случайную величину 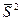– среднюю арифметическую исправленных дисперсий, взвешенную по числам степеней свободы:

, .

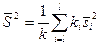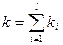На основе этой случайной величины строится критерий Бартлетта

,

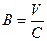где

,

.

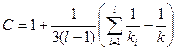Бартлетт установил, что случайная величина 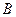при условии справедливости нулевой гипотезы распределена приближенно как 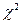с с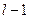тепенями свободы. Должно также выполняться условие

,

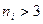т.е. объем каждой из выборок должен быть не меньше 4.

Критическую область строят правостороннюю. При этом, исходят из требования, чтобы вероятность попадания критерия в эту область(в предположении справедливости нулевой гипотезы) была равна принятому уровню значимости:

.

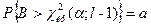Критическую точку 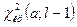находят из таблицы приложения 5, по уровню значимости 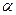и числу степеней свободы 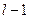. Тогда правосторонняя критическая область определяется неравенством

,

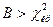а область принятия гипотезы – неравенством

.

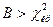Наблюдаемое значение критерия Бартлетта будем обозначать через .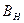

Правило проверки нулевой гипотезы будет следующим. Для того чтобы при заданном уровне значимости 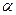проверить нулевую гипотезу об однородности дисперсий нормальных совокупностей, надо вычислить наблюдаемое значение критерия Бартлетта 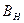. Затем, по таблице критических точек распределения 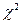найти критическую точку. Если окажется, что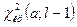

,

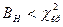то нет оснований отвергать нулевую гипотезу. В противном случае она отвергается.

В учебнике приведены конструктивные замечания по критерию Бартлетта. Приведем их.

Замечание 2. Константа , входящая в критерий Бартлетта, всегда больше единицы. Это обстоятельство следует учитывать при расчетах.

Замечание 3. Критерий Бартлетта весьма чувствителен к отклонениям распределений от нормального, поэтому к выводам, полученным по этому критерию, надо относиться с осторожностью(либо достоверно проверять, что совокупности распределены приближенно нормально).

Пример 5. Даны три независимые выборки из нормальных генеральных совокупностей:

,

,

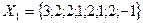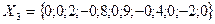
При уровне значимости 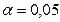проверить гипотезу об однородности дисперсий (критическая область односторонняя).

Решение. Опуская подробности расчетов, сведем предварительные результаты табл. 1

Табл.1. Расчетная таблица к примеру 5

№№Выборки і	Объем вы- борки	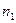Число степеней свободы	Исправлен-ная дис- персия
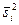
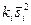
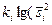
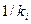
			1,428571		0,154902	1,084314	0,142857
			0,715636	7,156364	-0,14531	-1,45308	0,1
			1,2	9,6	0,079181	0,63345	0,125
∑		k =25		26,75636		0,264688	0,367857

Используя расчетную табл. 1, найдем значение средней арифметической исправленных дисперсий, взвешенной по числам степеней свободы:

Вычислим

и из таблице приложения 5, по уровню значимости 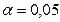и числу степеней свободы

найдем критическую точку

.

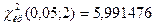Т.к.

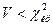
и, учитывая, что , получим

.

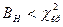Значит нет оснований отвергать нулевую гипотезу. Иными словами, исправленные выборочные дисперсии различаются незначимо.

Замечание 4. Если требуется оценить генеральную дисперсию, то при условии однородности дисперсий целесообразно принять в качестве ее оценки среднюю арифметическую исправленных дисперсий, взвешенную по числам степеней свободы, т.е.

.

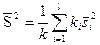Судя по примеру 5, в качестве оценки генеральной дисперсии целесообразно принять 1,070255.

4.Рассмотрим задачу сравнения нескольких (более двух) дисперсий нормальных генеральных совокупностей по выборкам одинакового объема.

Итак, пусть генеральные совокупности Х ₁ ,Х ₂... ,Х _l распределены нормально. Из этих совокупностей извлечено l независимых выборок одинакового объема п и по ним найдены исправленные выборочные дисперсии 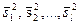все с одинаковым числом степеней свободы 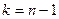. Необходимо по исправленным дисперсиям при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

Иными словами, требуется установить, значимо или незначимо различаются исправленные выборочные дисперсии.

Замечание 5. Рассматриваемую задачу можно решать, используя критерий Фишера – Снедекора, т.е. сравнивая наибольшую и наименьшую дисперсии. Если окажется, что различие между ними незначимо, то подавно незначимо и различие между остальными дисперсиями. Недостаток этого метода состоит в том, что информация, которую содержат остальные дисперсии, кроме наименьшей и наибольшей, не учитывается. Можно также применить критерий Бартлетта. Однако будет известно лишь приближенное распределение этого критерия. Поэтому предпочтительнее использовать критерий Кочрена, распределение которого найдено точно.

В качестве критерия проверки нулевой гипотезы примем критерий Кочрена – отношение максимальной исправленной дисперсии к сумме всех исправленных дисперсий:

.

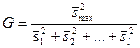Распределение этой случайной величины зависит только от числа степеней свободы 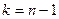и количества выборок l.

Критическую область строят правостороннюю, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:

.

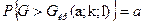Критическую точку 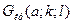находят по таблице приложения 8, и тогда правосторонняя критическая область определяется неравенством 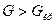, а область принятия нулевой гипотезы – неравенством .

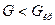Сформулируем правило проверки нулевой гипотезы. Чтобы при заданном уровне значимости α проверить гипотезу об однородности дисперсий нормально распределенных совокупностей, надо вычислить наблюдаемое значение критерия 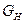и по таблице найти критическую точку. Если , то нет оснований отвергать нулевую гипотезу. В противном же случае ее отвергают.

11.3. Проверка статистических гипотез о равенстве средних

«Чем занимаются математики, как не

порядком и отношением?»

Аристотель

«…Чистый математик, как музыкант,-

свободный творец собственного мира

упорядоченной красоты».

Б. Рассел

Предыдущий параграф был посвящен задачам проверки гипотез о равенстве дисперсий. В настоящем же параграфе мы научимся проверять гипотезы о равенстве средних. Будут рассмотрены следующие вопросы:

1.Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны. Случай независимых выборок.

2.Сравнение двух произвольно распределенных генеральных совокупностей, Случай больших независимых выборок.

3.Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы. Случай малых независимых выборок.

4. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности.

5.Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями. Случай зависимых выборок.

1.На практике часто возникает необходимость сравнить средние статистических совокупностей. Рассмотрим вопрос сравнения средних двух нормальных генеральных совокупностей, дисперсии которых известны. Нами будет рассмотрен случай независимых выборок.

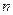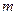Итак, пусть генеральные совокупности Х и У распределены нормально и их дисперсии известны(например, из предшествующего опыта или найдены теоретически). По независимым выборкам объема и , соответственно, извлеченным из этих совокупностей, рассчитаны выборочные средние и 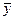. Необходимо по выборочным средним при заданном уровне значимости 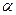проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т.е.

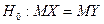
Т.к. выборочные средние являются несмещенными оценками генеральных средних (т.е. 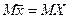, ), то нулевую гипотезу можно записать так:

.

Т.о. требуется проверить, что математические ожидания выборочных средних равны между собой. Такая задача ставится потому, что, как правило, выборочные средние оказываются различными. Возникает вопрос: значимо или незначимо различаются они?

Если окажется, что нулевая гипотеза справедлива, т.е. генеральные средние одинаковы, то различие выборочных средних незначимо и объясняется случайными причинами (например, случайным отбором элементов выборки). Так, если физические величины имеют одинаковые истинные размеры, а средние арифметические результатов измерений этих величин различны, то это различие незначимое. Если же нулевая гипотеза отвергнута, т.е. генеральные средние неодинаковы, то различие выборочных средних значимо и не может быть объяснено случайными причинами, а объясняется тем, что сами генеральные средние (математические ожидания) различны. Например, если среднее арифметическое результатов измерений первой физической величины значимо отличается от среднего арифметического 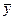результатов измерений второй физической величины, то это означает, что истинные размеры (математические ожидания) этих величин различны.

В качестве критерия проверки нулевой гипотезы примем случайную величину

.

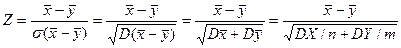Критерий Z –нормированная нормальная случайная величина. Действительно, величина распределена нормально, так как является линейной комбинацией нормально распределенных величин и 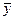. Сами эти величины распределены нормально как выборочные средние, найденные по выборкам, извлеченным из нормальных генеральных совокупностей. Z – нормированная величина, т.к. при справедливости нулевой гипотезы 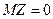, а поскольку выборки независимы, то .

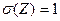Как и ранее, критическая область строится в зависимости от конкурирующей гипотезы.

Случай первый: нулевая гипотеза

,

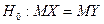конкурирующая гипотеза

.

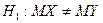В этом случае строят двустороннюю критическую область. При этом требуют, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна заданному уровню значимости .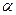

Наибольшая мощность критерия достигается тогда, когда левая и правая критические точки выбраны так, что вероятность попадания критерия в каждый из двух интервалов критической области равна α/2:

,

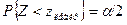Т.к. Z – нормированная нормальная величина, а распределение такой величины симметрично относительно нуля, то критические точки величины симметричны относительно нуля. Обозначим правую границу двусторонней критической области через 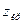, тогда левая граница равна 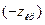. Поэтому достаточно найти правую границу, чтобы найти саму двустороннюю критическую область 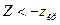, 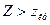и область принятия нулевой гипотезы .

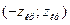Интегральная функция Лапласа 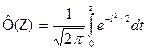определяет вероятность попадания нормированной нормальной случайной величины 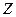в интервал :

В силу симметрии этого распределения относительно нуля, имеем

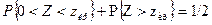
Т.е.

,

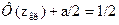откуда получаем

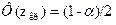
Теперь, обозначив через Z_н наблюдаемое значение критерия (т.е. вычисленное по данным выборки), сформулируем правило проверки нулевой гипотезы.

Для того, чтобы при заданном уровне значимости α проверить нулевую гипотезу о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе 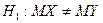, надо вычислить наблюдаемое значение критерия

.

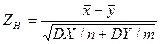Затем по таблице интегралов функции Лапласа найти критическую точку 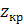из условия

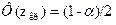
Если окажется, что

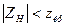
то нет оснований отвергать нулевую гипотезу. В противном же случае ее нужно отвергнуть.

Если использовать статистические функции из Microsoft Excel, то для нахождения 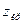надо вычислять

.

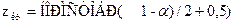В Maple 6 для нахождения 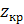вычисляют

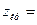stats[statevalf,icdf,normal[0,1]]((1-α)/2+0.5).

Пример 1. По двум независимым выборкам, объемы которых соответственно равны и , и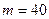звлеченным из нормальных генеральных совокупностей, найдены выборочные средние 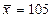и 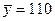. Генеральные дисперсии известны и . Требуется при уровне значимости 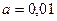проверить нулевую гипотезу 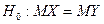, при конкурирующей гипотезе .

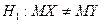Решение. Найдем наблюдаемое значение критерия

По условию, конкурирующая гипотеза имеет вид , поэтому критическая область – двусторонняя. Найдем правую критическую точку из условия

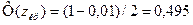
По таблице интегральной функции Лапласа приложения 2 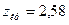. Если использовать Microsoft Excel, то

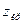= НОРМСТОБР((1-0,01)/2+0,5)=2,5758.

При использовании Maple 6, имеем

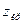= stats[statevalf,icdf,normal[0,1]]((1-),01/2+0,5)=2.5758.

Т.к. 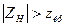, то нулевая гипотеза отвергается. Иными словами, выборочные средние различаются.

В качестве второго случая рассмотрим нулевую гипотезу 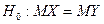и конкурирующую гипотезу 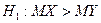. На практике такой случай имеет место, если профессиональные соображения позволяют предположить, что генеральная средняя одной совокупности больше генеральной средней другой. Например, пусть генеральная средняя характеризует объем выпуска продукции. Если технологический процесс был усовершенствован, то естественно допустить, что это приведет к увеличению объема выпуска продукции.

В этом случае строят правостороннюю критическую область. Причем, исходят из требования, чтобы вероятность попадания критерия в эту область (в предположении справедливости нулевой гипотезы) была равна заданному уровню значимости:

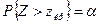
Критическая точка находится следующим образом. Воспользовавшись симметрией функции распределения стандартной нормальной случайной величины относительно нуля, получаем

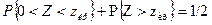
Т.о.

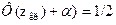
откуда имеем

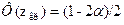
Из последнего соотношения по таблицам интегральной функции Лапласа или программными средствами находят точку .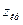

Определим правило проверки нулевой гипотезы. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу 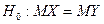о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе

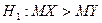, надо вычислить наблюдавшееся значение критерия

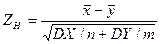
и по таблице интегральной функции Лапласа найти критическую точку 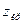из условия

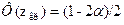
Если окажется, что , то нет оснований отвергать нулевую гипотезу. В противном же случае ее нужно отвергнуть.

Пример 2. По двум независимым выборкам, объемы которых соответственно равны 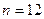и , и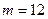звлеченным из нормальных генеральных совокупностей, найдены выборочные средние 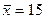и 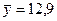. Генеральные дисперсии известны: 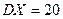и . При уровне значимости 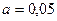проверить нулевую гипотезу 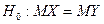при конкурирующей гипотезе .

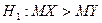Решение. Найдем наблюдаемое значение критерия:

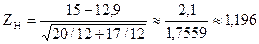
Найдем критическую точку 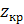из условия

.

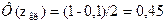По таблице интервальной функции Лапласа (см. приложение 2) 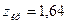. Т.к. , то нет оснований отвергнуть нулевую гипотезу. Другими словами, выборочные средние различаются незначимо.

Третий случай: нулевая гипотеза 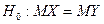, конкурирующая гипотеза 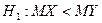. Этот случай подразумевает построение левосторонней критической области. При этом нужно исходить из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:

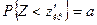
Т.к. критерий 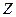распределен симметрично относительно нуля, то .

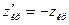Правило проверки нулевой гипотезы следующим. При конкурирующей гипотезе 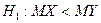надо вычислить . Из таблицы интегральной функции Лапласа найти «вспомогательную точку» 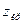по равенству 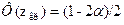и положить 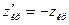. Если окажется, что 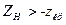, то нет оснований отвергать нулевую гипотезу. В противном же случае ее нужно отвергнуть.

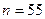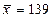Пример 3. По двум независимым выборкам, объемы которых, соответственно равны и , извлеченным из нормальных генеральных совокупностей, найдены выборочные средние и 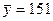. Генеральные дисперсии известны 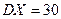и 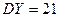. При уровне значимости 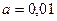проверить нулевую гипотезу 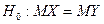, при конкурирующей гипотезе .

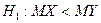Решение. Найдем наблюдаемое значение критерия:

.

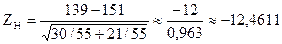Определи «вспомогательную точку» 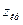из условия

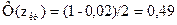
По таблице интегральной функции Лапласа приложения 2 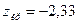. Т.о., 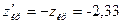В силу того, что , то нулевую гипотезу следует отвергнуть. Другими словами, выборочная средняя 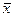значимо меньше выборочной средней .

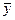Мы закончили рассмотрение случая, в котором предполагалось, что генеральные совокупности X и Y распределены нормально и их дисперсии известны. При этих предположениях, в случае справедливости нулевой гипотезы о равенстве средних и независимых выборках, критерий 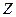распределен нормально с параметрами 0 и 1. Если же хотя бы одно из перечисленных требований не выполняется, то описанный метод сравнения средних неприменим.

2.В то же время, если независимые выборки имеют большой объем (не менее 30 каждая), то выборочные средние 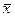и 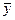распределены приближенно нормально. Выборочные дисперси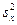и и являются достаточно хорошими оценками генеральных дисперсий DX и DY, соответственно. В этом смысле их можно считать известными приближенно. Тогда критерий

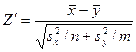
распределен приближенно нормально с параметрами 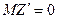(при условии справедливости нулевой гипотезы) и 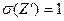(если выборки независимы). В итоге мы можем сделать следующие выводы: 1) если генеральные совокупности распределены нормально, а дисперсии их неизвестны; 2) если генеральные совокупности не распределены нормально и дисперсии их неизвестны, причем выборки имеют большой объем и независимы, тогда можно сравнивать средние так, как описано ранее, заменив при этом точный критерий приближенным критерием. Т.е. наблюдаемое значение приближенного критерия будет равно

.

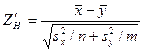Замечание 1. Поскольку рассматриваемый критерий – приближенный, к его выводам следует относиться осторожно.

Пример 4. По независимым выборкам, объемы которых, соответственно равны и 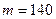, найдены выборочные средние 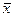=30 и 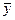=29 и выборочные дисперсии 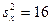, 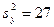. Необходимо при уровне значимости 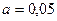проверить нулевую гипотезу 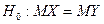, при конкурирующей гипотезе .

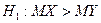Решение. Найдем наблюдаемое значение критерия:

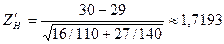
По условию конкурирующая гипотеза имеет вид 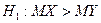. Следовательно, критическая область – правосторонняя. Найдем критическую точку 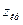из условия

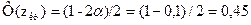
По таблице интегральной функции Лапласа (см. приложение 2) 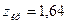. Т.к., 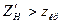то нулевая гипотеза отвергается. Другими словами, выборочные средние различаются значимо.