Электрический колебательный контур

ИЗУЧЕНИЕ РЕЗОНАНСА В L-R-C ЦЕПИ

ФЭЛ-1

Тверь, 2013 г

Лабораторная работа.

Изучение явления резонанса в последовательном и параллельном колебательном контуре

Цель работы: Изучение установившихся вынужденных колебаний в цепях переменного тока. Получение зависимостей амплитуды тока (при параллельном включении элементов контура) и напряжения на конденсаторе (при последовательном включении элементов контура) колебательного контура от частоты электродвижущей силы внешнего источника. Построение амплитудно-частотных характеристик колебательных контуров с последовательным и параллельным соединениями их элементов.

Теоретическое описание.

Электрический колебательный контур.

Колебательная система, использующаяся в радиотехнических устройствах, представляет собой электрическую цепь, состоящую из емкости С, индуктивности L и активного сопротивления R.

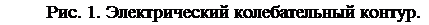
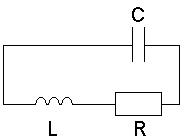Наличие сопротивления R обуславливает потери электрической энергии в контуре. Такой контур является затухающим гармоническим осциллятором, для которого справедливо следующее дифференциальное уравнение свободного колебательного процесса:

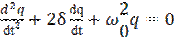, (1.1)

где q – заряд конденсатора, 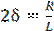(d - коэффициент затухания контура);

- круговая частота свободных электрических колебаний контура.

С течением времени свободный колебательный процесс в контуре будет затухать. Для получения незатухающих колебаний необходимо непрерывно пополнять запас энергии контура, чтобы скомпенсировать потери. С этой целью контур подключается к генератору переменного тока. Незатухающие колебания, возникающие в контуре, называются вынужденными, поскольку их частота определяется частотой генератора. В этом случае дифференциальное уравнение колебательного процесса примет вид:

(1.2)

В настоящей задаче исследуются вынужденные колебания в колебательном контуре, элементами которого являются конденсатор C, индуктивность L и активное сопротивление R, соединенные последовательно (рис. 1,а) или параллельно (рис. 1,б) с источником питания. При этом в качестве источника питания используется либо генератор переменной ЭДС 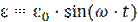(рис. 1,а), либо генератор переменного тока 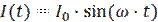(рис. 1,б).

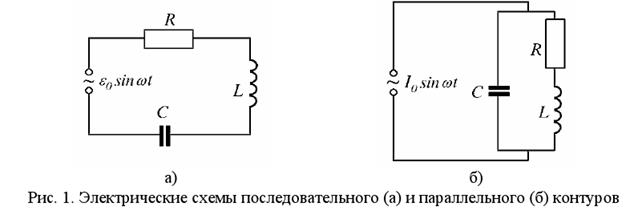Последовательное соединение элементов контура.

Рассмотрим электрическую цепь, включающую в себя внешний источник, ЭДС которого меняется по гармоническому закону 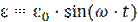конденсатор C, индуктивность L и активное сопротивление R (см. рис. 1а). Записывая закон Кирхгофа для этой цепи, получим уравнение вынужденных колебаний в контуре:

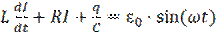(1.3)

где I - ток, протекающий в контуре; q - заряд на пластине конденсатора; ε₀ - амплитуда напряжения источника ЭДС; ω - частота источника ЭДС. Так как сила тока 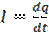, то уравнение (1.3) можно записать в следующем виде

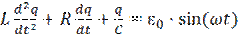(1.4)

Разделим обе части уравнения (1.4) на L и введя обозначения

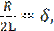
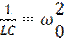(1.5)

где ω₀ - собственная частота колебательного контура в отсутствие затухания, δ - коэффициент затухания колебаний.

С учетом обозначений (1.5) уравнение (1.4) может быть преобразовано к следующему виду:

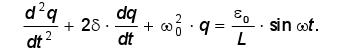(1.6)

Для установившихся колебаний решение этого уравнения будет выглядеть следующим образом:

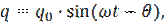(1.7)

где

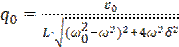(1.8)

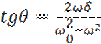(1.9)

Используя выражение (1.7) для q, можно установить закон изменения тока в цепи:

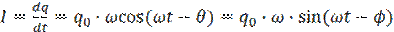(2.0)

где 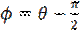- разность фаз между ЭДС и током в цепи, 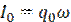- амплитуда колебаний силы тока в цепи а:

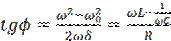(2.1)

С учетом (1.8) можно записать выражение для зависимости амплитуды тока в цепи от частоты ЭДС:

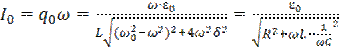(2.2)

Из формулы (2.2) видно, что амплитудное значение силы тока зависит от частоты ω. Рассмотрим полученные результаты подробнее. При ω = 0 амплитуда тока I₀=0. С ростом частоты I₀ возрастает и при 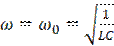амплитуда тока достигает максимального значения 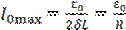, разность фаз φ при этом равна нулю. При дальнейшем увеличении частоты I₀ уменьшается, и при ω → ∞ амплитуда тока I₀ → 0. В итоге зависимость I₀ (ω) имеет вид, представленный на рис. 2 (для двух значений активного сопротивления). Эта зависимость получила название амплитудночастотной характеристики контура.

Из рис. 2 видно, что чем меньше R (меньше коэффициент затухания δ), тем больше I ₀ и тем «острее» максимум кривой.

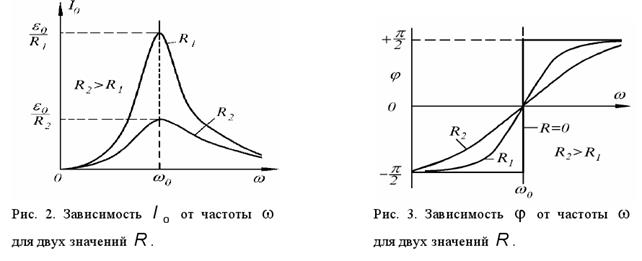На рис.3 приведены зависимости разности фаз между ЭДС и током в цепи φ от частоты ω. Видно, что при частотах, близких к нулю, разность близка к 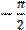(говорят, что напряжение отстает по фазе от тока на 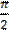), при больших частотах разность фаз стремится к 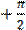(напряжение опережает ток по фазе на 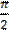). При частоте ω = ω₀ разность фаз равна нулю. Из рис.3 видно, что чем меньше R, тем быстрее изменение φ вблизи частоты ω = ω₀, в предельном случае при R = 0 фаза изменяется скачком при ω = ω₀ .

Найдем теперь зависимость напряжения на конденсаторе 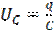от частоты ω. Так как 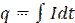, то, проинтегрировав выражение (2.0), получим:

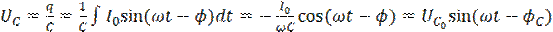(2.3)

где

(2.4)

– амплитуда колебаний напряжения на конденсаторе, 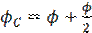- разность фаз между ЭДС и напряжением на конденсаторе. При ω= ω₀ получим:

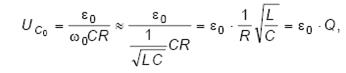
(2.5)

где 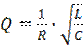- добротность контура. Значение добротности характеризует величину потерь энергии в контуре - чем меньше потери, тем больше добротность. Из формулы (2.5) видно, что при ω = ω₀ напряжение на конденсаторе в Q раз больше ЭДС источника. Это явление носит название резонанса напряжений. Можно показать, что амплитуда колебаний напряжения на индуктивности 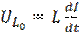при ω = ω₀ также будет равна ε₀ ∙ Q, но при этом напряжение на индуктивности будет меняться в противофазе с напряжением на конденсаторе.

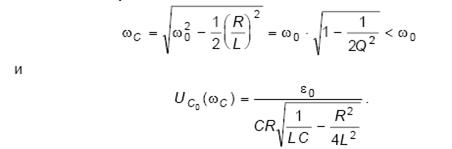Из формулы (2.4) можно найти частоту ω_C, при которой напряжение на конденсаторе будет максимальным. Для этого надо решить уравнение 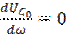. После несложных, но громоздких преобразований можно получить:

(2.6)

(2.7)

При Q>>1 можно записать ω_С ≈ ω₀, а .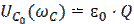

По определению, добротность 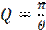где θ - логарифмический декремент затухания свободных колебаний в контуре. В свою очередь, θ = δT, где (затухание мало, поэтому 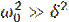), и после несложных преобразований можно получить формулу 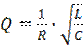. Также для добротности часто приводят формулу 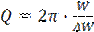, где W- энергия, запасенная в контуре, ΔW — потери энергии в контуре за период колебаний.

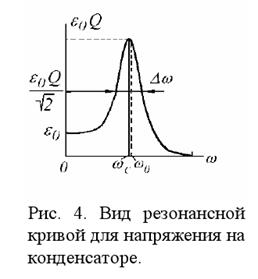Таким образом, измеряя напряжение на конденсаторе на резонансной частоте, можно определить добротность контура Q. На рис. 4 приведен вид зависимости амплитуды напряжения на конденсаторе от частоты ЭДС внешнего источника.

При ω = 0 U_C0 = ε₀, по мере увеличения частоты U_C0 растет и при 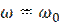достигает своего максимального значения 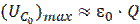после чего начинается монотонное убывание напряжения до нуля. Обратим внимание на тот факт, что частота ω_C, при которой амплитуда колебаний напряжения на конденсаторе максимальна, несколько меньше частоты ω₀, для которой максимальна амплитуда силы тока.

Обычно вводится понятие ширины резонансной кривой ∆ω - это диапазон частот, для которых амплитуда напряжения отличается от амплитуды напряжения в резонансе не более, чем в 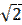раз.

Можно показать, что для ∆ω << ω₀ справедливо соотношение 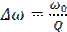или 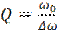. Таким образом, определяя ширину резонансной кривой, можно также найти добротность контура Q.

График зависимости разности фаз между напряжением источника ЭДС и напряжением на конденсаторе будет иметь такой же вид, как на рис. 3, только «приподнятый» на , т. к. 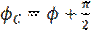. Иными словами, в точке резонанса, когда ток и напряжение источника совпадают по фазе, напряжение на конденсаторе будет отставать по фазе от напряжения источника на .

Напряжение на конденсаторе всегда (а не только при резонансе) отстает по фазе от тока, протекающего через конденсатор, на , в свою очередь, напряжение на индуктивности всегда опережает по фазе ток на .